5.7. Диффузионная загонка
В технологии ИМС диффузия легирующих примесей осуществляется обычно в две стадии. Первая стадия – загонка – проводится из примесно-силикатного стекла с постоянной поверхностной концентрацией, равной, как правило, предельной растворимости примеси в кремнии при температуре диффузии: Cпов = Cпред (см. прил. 3). Решение уравнения диффузии из бесконечного источника при D = const и Спов = const имеет вид
(5.16)
Дополнительная функция ошибок erfc в (5.16) аппроксимируется следующими аналитическими выражениями:
с погрешностью не хуже 18 % при
.
Наиболее точная аппроксимация
дополнительной функции ошибок с
погрешностью не более 1.5 · 10–5
% при любых z дается в [17]:
где
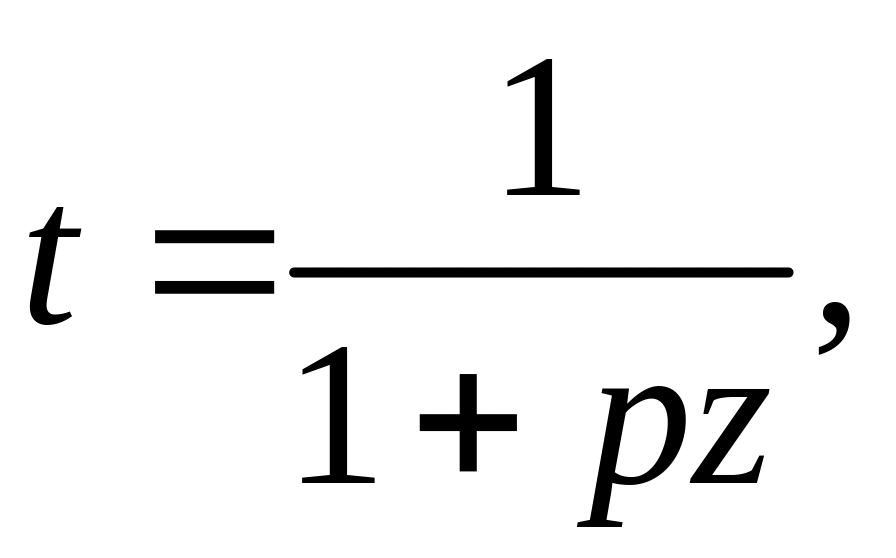p =
0.3275911, a
= 0.2548296,
b =
–0.2844967, c
= 1.4214137,
d = –1.4531520,
e =
1.0614054.
Во многих технологических операциях изготовления ИМС используется диффузионное или ионное легирование с высокой концентрацией легирующей примеси (C > ni), например при разделительной диффузии, создании скрытых слоев и областей эмиттера, подлегировании коллектора в технологии биполярных ИМС, при формировании областей стока и истока, стоп-слоев, подлегировании омических контактов в технологии МОП ИМС. Во всех этих случаях коэффициент диффузии легирующей примеси является функцией локальной концентрации примеси D = D(C).
Согласно современным представлениям [6], [14] коэффициент диффузии легирующей примеси может быть представлен в виде
(5.17)
где
– парциальные коэффициенты диффузии
примеси посредством, соответственно,
нейтральных, положительных, отрицательных
и дважды отрицательно заряженных
собственных точечных дефектов (вакансий
и/или собственных междоузельных атомов)
в собственном или слаболегированном
полупроводнике. Значения параметров
температурной зависимости парциальных
коэффициентов диффузии для основных
легирующих примесей в кремнии приведены
в прил. 7.
Согласно выражению (5.17) коэффициент диффузии легирующей примеси является функцией концентрации примеси через концентрацию носителей заряда, т. е. D = D(C(n, p)). В этом случае необходимо пользоваться уравнением диффузии в форме
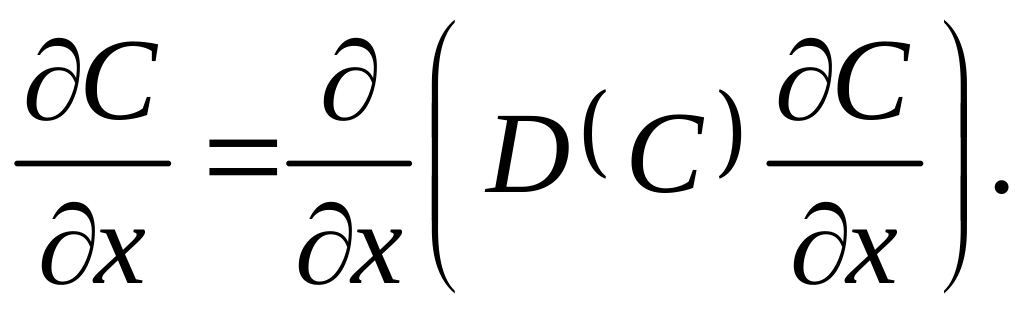(5.18)
Решение дифференциального уравнения вида (5.18) при D const в общем случае осуществляется численными методами.
5.8. Диффузионная разгонка
Вторая стадия диффузии – разгонка – проводится после удаления с поверхности источника примеси (примесно-силикатного стекла) при более высоких температурах и длительностях, чем загонка, как правило, в окислительной среде. На этой стадии создается легированный слой с требуемыми глубиной и поверхностным сопротивлением, а на поверхности вырастает защитный слой диоксида кремния заданной толщины. В этом случае имеет место диффузия из ограниченного источника. При D = const и без учета сегрегации решение уравнения диффузии имеет вид
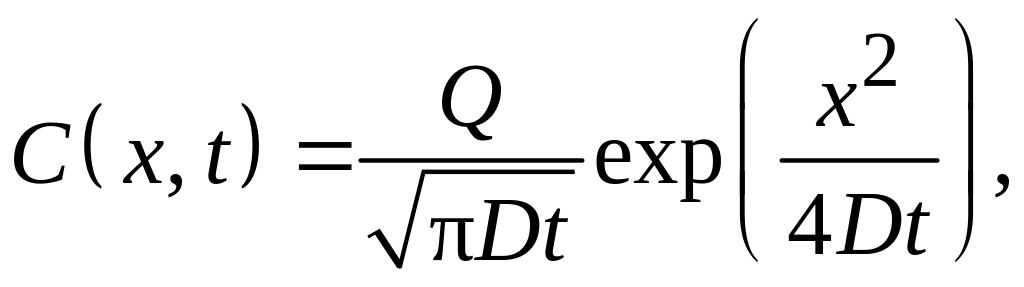
где
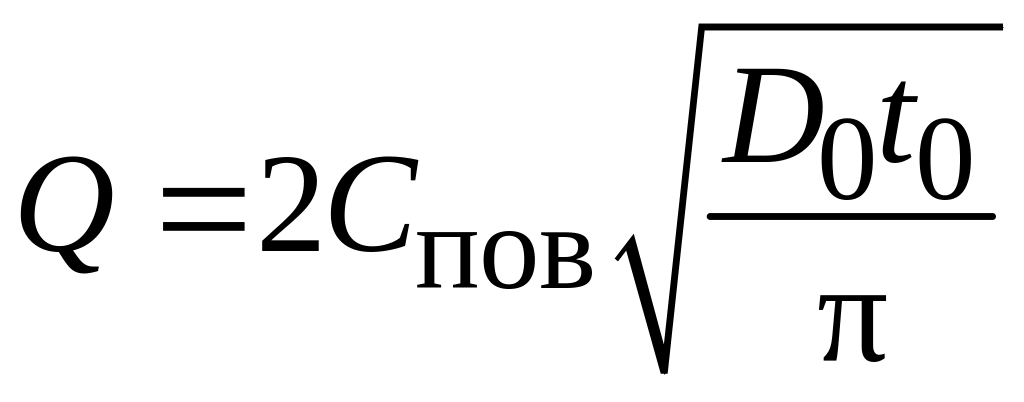– количество примеси, введенное на 1-й
стадии диффузии.
Аналогичным образом проводятся активация и отжиг имплантированных слоев (постимплантационный отжиг) после внедрения ионов легирующих примесей. В этом случае при D = const и наличии отражающей границы на поверхности распределение примеси по глубине принимает вид
где Q – доза имплантации.
При проведении второй стадия диффузии в окислительной среде необходимо учитывать сегрегацию примеси на движущейся границе раздела Si–SiO2, для чего необходимо решать уравнение вида (5.13) с граничным условием (5.14). При высоких концентрациях примеси коэффициент диффузии становится функцией концентрации вида (5.17) и необходимо проводить численное решение уравнения диффузии с движущейся границей.