
- •Технологическое моделирование фрагмента имс
- •1. Задание на курсовую работу и исходные данные
- •2. Требования к оформлению и содержанию курсовой работы
- •3. Последовательность выполнения курсовой работы
- •3.1. Выбор электрической схемы фрагмента имс
- •3.2. Топологический чертеж и поперечное сечение кристалла
- •3.3. Разработка технологического маршрута
- •3.4. Моделирование операций технологического маршрута
- •3.5. Заключение курсовой работы
- •4. Структуры биполярных и моп имс
- •4.1. Биполярный планарно-эпитаксиальный транзистор
- •4.2. Биполярная имс с изоляцией p–n-переходом
- •4.3. Изопланарная биполярная имс
- •4.4. Моп имс с металлическим затвором
- •4.5. Моп имс с поликремниевым затвором
- •4.7. Кмоп имс
- •4.8. Дмоп имс
- •5. Моделирование процессов технологии имс
- •5.1. Ионная имплантация
- •5.2. Ионная имплантация через пленку
- •5.3. Концентрация носителей заряда в сильнолегированных слоях
- •5.4. Термическое окисление
- •5.5. Перераспределение примесей при термическом окислении
- •5.7. Диффузионная загонка
- •5.8. Диффузионная разгонка
- •5.9. Совместная диффузия легирующих примесей
- •5.10. Расчет положения p–n-перехода и слоевого сопротивления
- •Список литературы
- •1. Параметры распределения Пирсона для ионов b, p, As, Sb в Si [9]
- •2. Параметры распределения Пирсона для ионов b, p, As, Sb в SiO2 [9]
- •3. Предельные растворимости легирующих примесей в кремнии, см–3 [6]
- •4. Параметры температурной зависимости констант скорости термического окисления кремния ориентации (111) [6]
- •5. Коэффициенты сегрегации легирующих примесей в системе SiO2–Si(111)
- •6. Параметры температурной зависимости коэффициентов испарения и диффузии легирующих примесей в кремнии
- •7. Параметры парциальных коэффициентов диффузии основных легирующих примесей в кремнии [6], [23]
- •8. Параметры концентрационной зависимости подвижности носителей заряда в кремнии [19]
- •Содержание
- •1 97376, С.-Петербург, ул. Проф. Попова, 5
5.5. Перераспределение примесей при термическом окислении
При термическом окислении происходит перераспределение примесей между полупроводником и растущим оксидом. При невысоких скоростях окисления, меньших скорости продвижения диффузионного фронта, отношение концентраций примеси в оксиде C(SiO2) и кремнии C(Si) на границе раздела устанавливается постоянным, равным коэффициенту сегрегации:
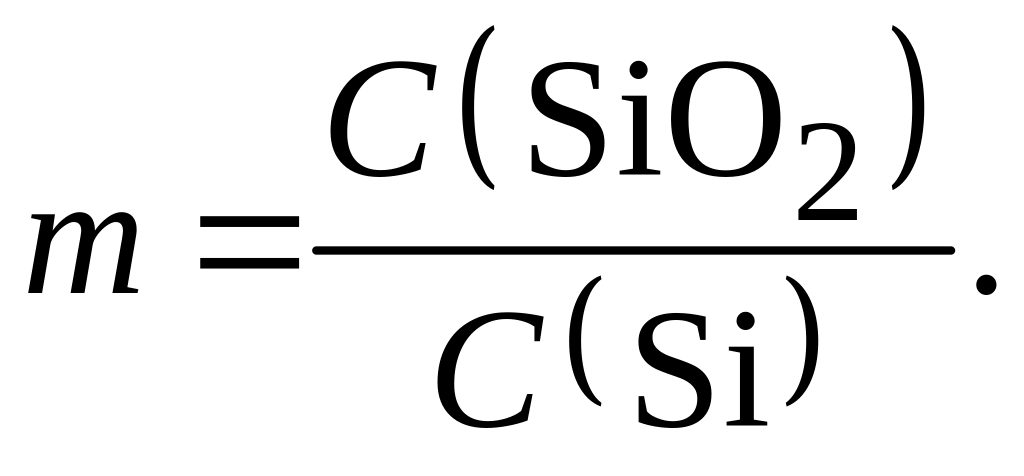
Если энергия образования оксида примеси больше, чем оксида кремния, то m < 1, примесь не захватывается оксидом, а оттесняется в кремний, накапливаясь на границе раздела (примеси P, As, Sb в Si). Если энергия образования оксида примеси меньше, чем оксида кремния, то наоборот: m > 1, примесь захватывается оксидом, поверхность кремния обедняется примесью (примеси В, Al в Si). Значения коэффициентов сегрегации для основных легирующих примесей в кремнии приведены в прил. 5.
В системе с движущейся границей раздела Si–SiO2 x = y – aw, где w – толщина оксида, a = 0.45 – отношение толщины окисленного кремния к толщине образовавшегося оксида. При постоянном коэффициенте диффузии примеси в кремнии D = const, а в оксиде Dокc = 0 уравнение диффузии принимает вид [14]
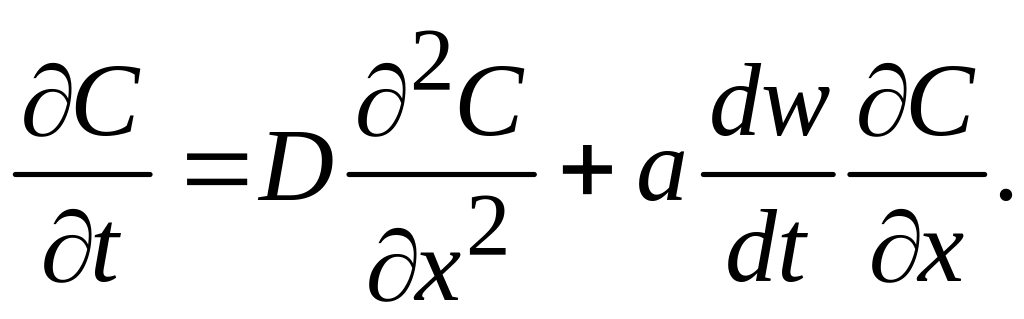 (5.13)
(5.13)
Начальное и граничное условия имеют вид
![]() при y
≥ 0,
при y
≥ 0,
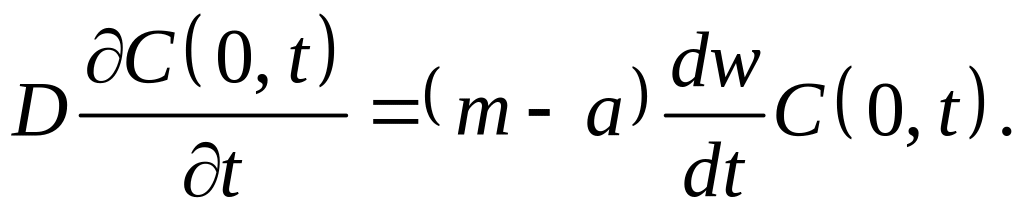 (5.14)
(5.14)
При параболическом законе окисления
(![]() )
задача имеет точное решение в интегральной
форме [15]:
)
задача имеет точное решение в интегральной
форме [15]:
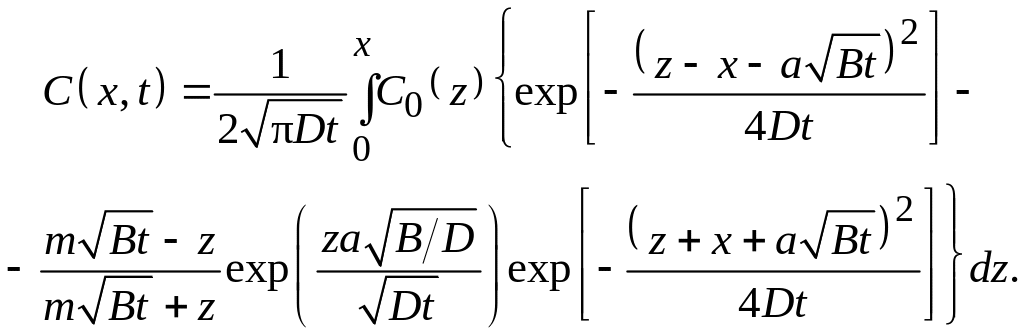
В случае однородного начального распределения легирующей примеси в кремнии (C(x, 0) = C0 = const) и отсутствия начального оксида (w(0) = 0) распределение примеси в кремнии после термического окисления описывается аналитическим выражением [14]
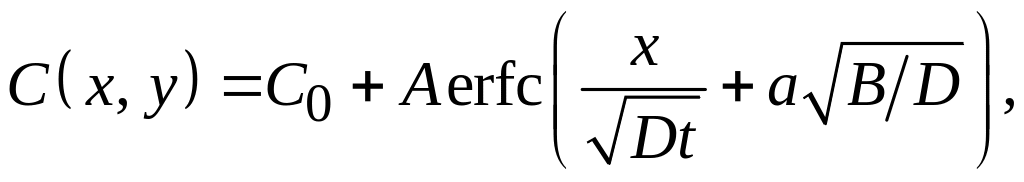

где x – координата, отсчитываемая от границы раздела Si–SiO2. Распределение концентрации примеси в оксиде по глубине при этом постоянно:
![]()
В случае неоднородного исходного распределения примеси по дополнительной функции ошибок (после первой стадии диффузии при C(0, t) = Спов = = const и D0 = const)

распределение примеси в кремнии после термического окисления описывается аналитическим выражением [14]
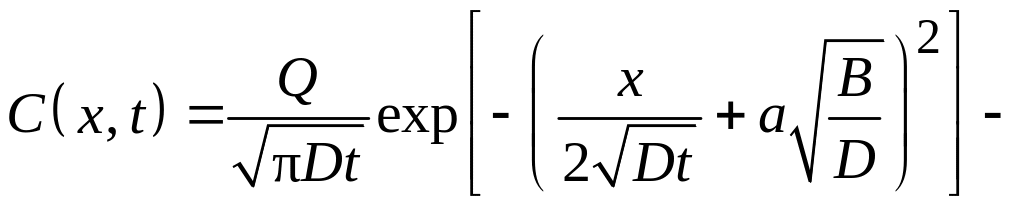
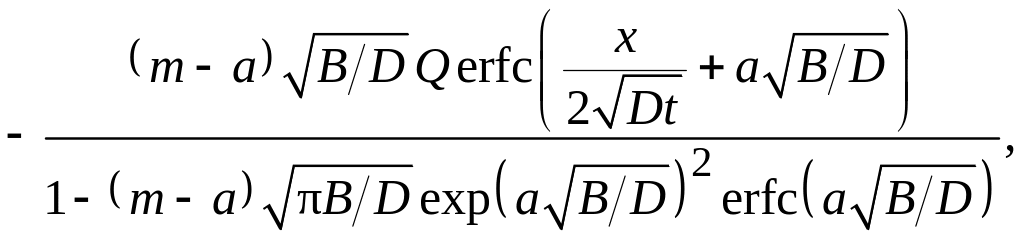
где Q – напомним, количество примеси в легированном слое, введенное на первой стадии диффузии:
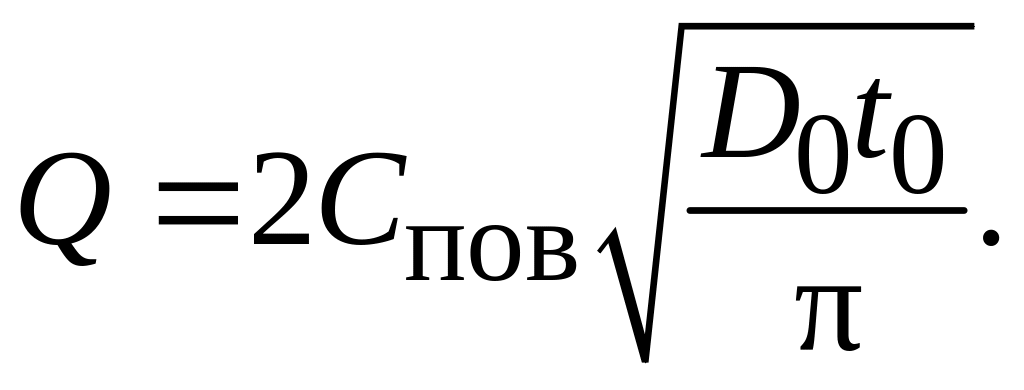
5.6. Решения уравнения диффузии при D = const
В ряде операций технологии ИМС используется диффузионное или ионное легирование с низкими концентрациями легирующих примесей (C < ni), например при создании карманов и подлегировании каналов в технологии МОП ИМС, создании резисторов и базы в технологии биполярных ИМС. В этих случаях коэффициент диффузии легирующей примеси не зависит от концентрации (D = const) и уравнение диффузии имеет вид
 (5.15)
(5.15)
В общем случае при произвольном начальном
распределении примеси C(x, 0) =
C0(x)
дифференциальное уравнение (5.15) имеет
решение в интегральной форме для
бесконечного пространства
![]() в виде
в виде
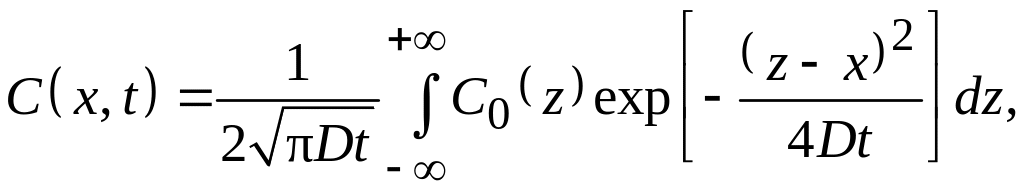
а для полубесконечного пространства
(![]() )
в виде
)
в виде
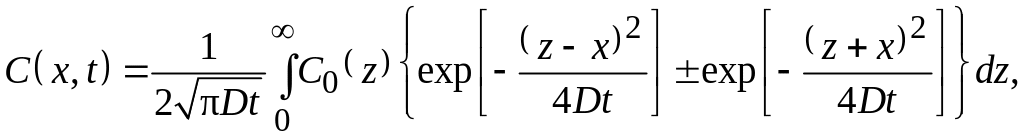
где z – переменная интегрирования,
знак плюс между экспонентами соответствует
отражающей границе при x = 0
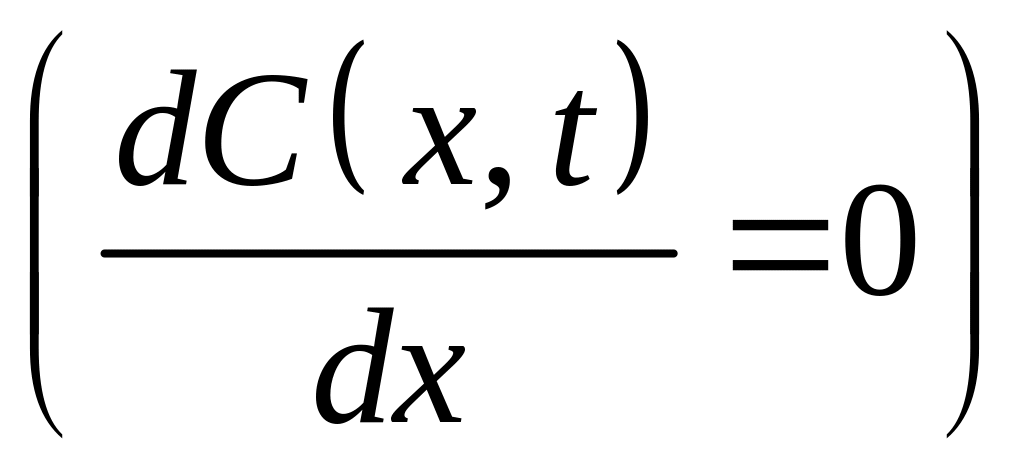 ,
а знак минус – поглощающей границе при
x = 0 (
,
а знак минус – поглощающей границе при
x = 0 (![]() ).
).
В отдельных частных
случаях уравнение диффузии (5.15) имеет
точные решения в виде аналитических
или известных табулированных функций:
erf(z),
erfc(z), exp(–z2),
где
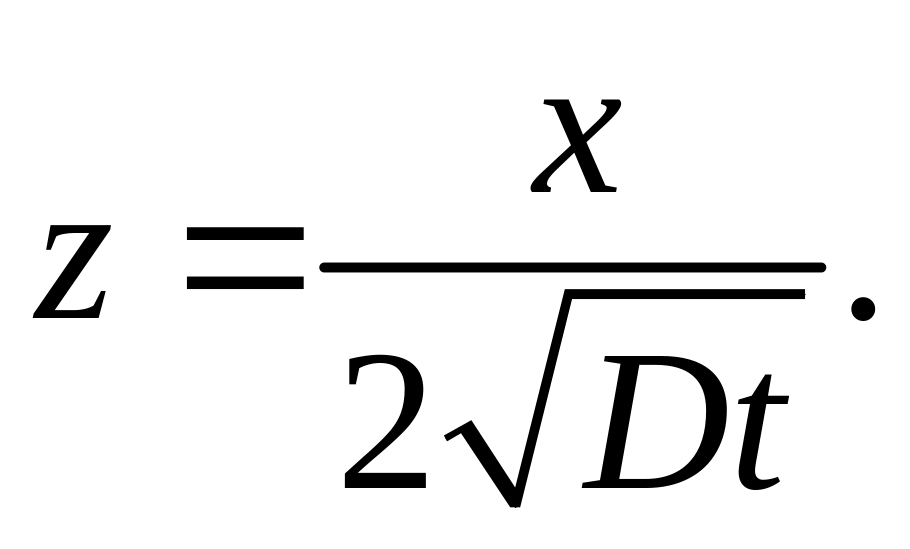 Функция ошибок определяется следующим
выражением:
Функция ошибок определяется следующим
выражением:
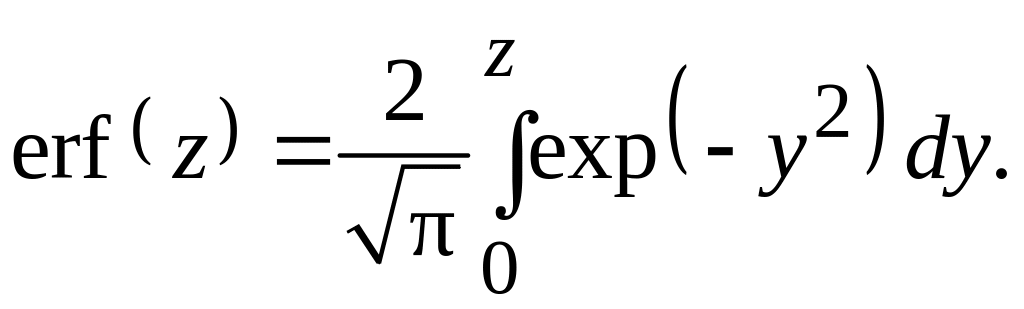
Дополнительная функция ошибок дополняет функцию ошибок до 1:
![]()
Дополнительная функция ошибок определяет распределение примеси по глубине:
1. При диффузии из бесконечного (постоянного) источника (C(0, t) = = Cпов = const) на этапе загонки легирующей примеси:
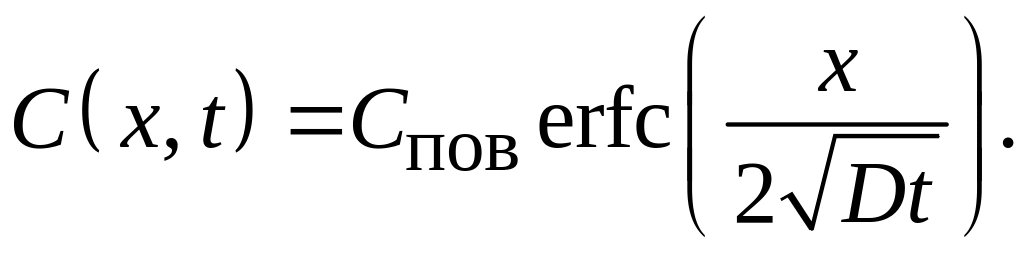
2. При диффузии из ограниченного источника
с количеством примеси Q и отражающей
границе при x = 0
 на этапе разгонки:
на этапе разгонки:
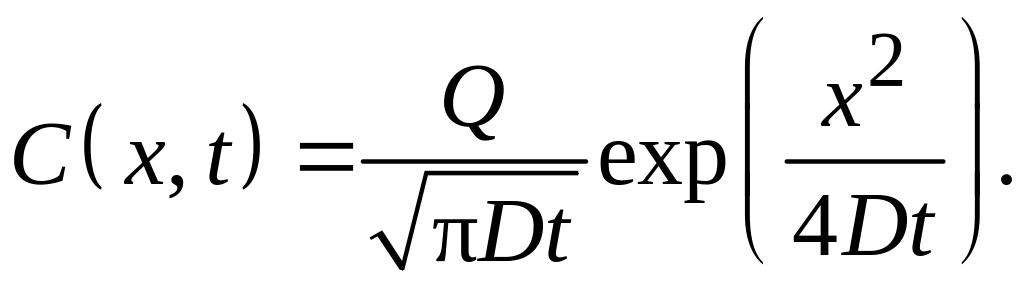
3. При диффузии в неограниченном теле из полубесконечного пространства с равномерным распределением примеси (C(x, 0) = C0 при x ≤ 0):
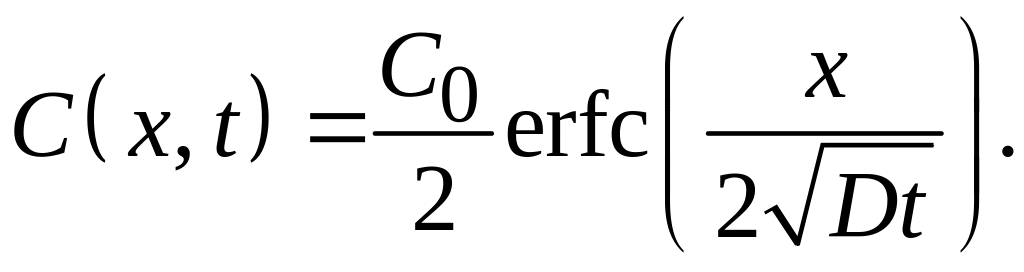
Этот случай имеет место в планарно-эпитаксиальной технологии ИМС при выращивании слаболегированных эпитаксиальных пленок на сильнолегированных подложках или скрытых слоях.
4. При диффузии из полуограниченного равномерно легированного тела (C(x, 0) = C0 при x ≥ 0) наружу (испарении) со связывающей (поглощающей) границей (C(0, t) = 0):
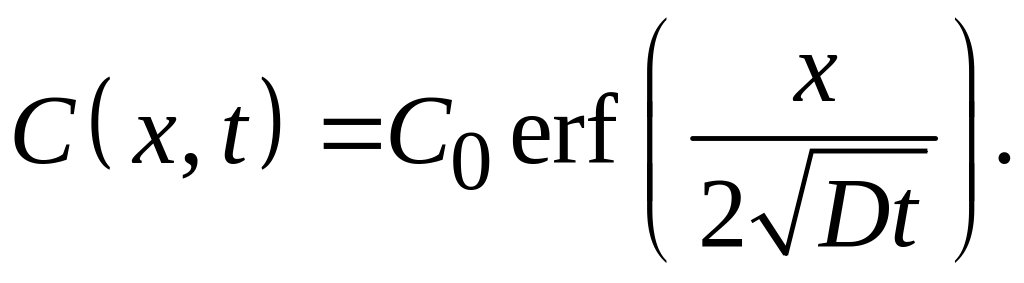
5. При наличии активационного барьера для испарения примеси граничное условие на поверхности имеет вид
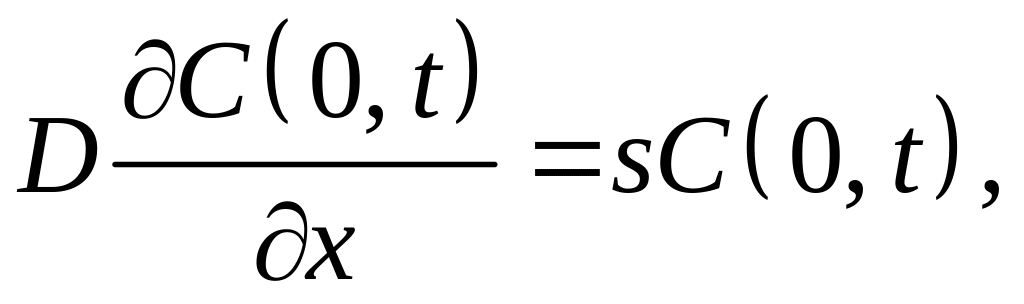
где s – коэффициент испарения примеси. Решение уравнения диффузии для полуограниченного тела с равномерным исходным легированием имеет в этом случае вид [16]

Возможность потерь и перераспределения примесей вследствие испарения необходимо учитывать при отжигах полупроводниковых подложек и легированных слоев с незащищенной поверхностью в вакууме, нейтральных средах (Ar, N2), а также при предэпитаксиальной обработке подложек в водороде. Параметры температурной зависимости коэффициентов испарения и определяемых совместно с ними коэффициентов диффузии легирующих примесей в кремнии приведены в прил. 6.
