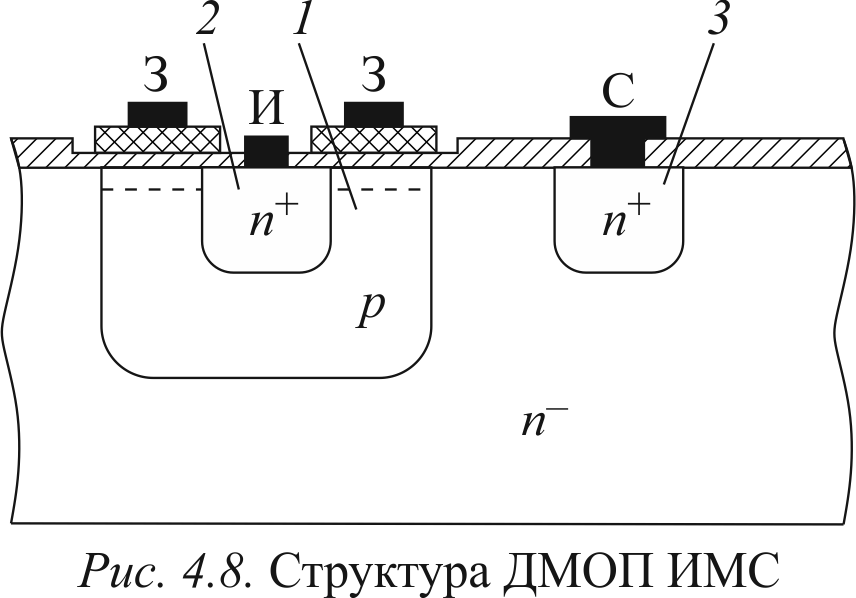
4.8. Дмоп имс

В структуре ДМОП ИМС (рис. 4.8) подзатворная p-область 1 и n⁺-об­ласть истока 2 формируются двойной (double) диффузией (или имплантацией) донорной (P или As) и акцепторной (B) примесей в одно окно в диоксиде

к

ремния на n^–-подложке. Этим достигается малая длина канала, равная примерно ширине базы вертикального n⁺–p–n^–-транзистора. Область n⁺-стока 3, которая может формироваться одновременно с об­ластью n⁺-истока, создается на некотором удалении от истока. Исток контактирует с индуцированным каналом, управляемым затвором, через n^-подложку и обогащенный поверхностный n⁺-слой. Последний образуется под действием положительного заряда в пленке диоксида кремния.

5. Моделирование процессов технологии имс

Целью технологического моделирования является построение адекватной модели технологического процесса для того, чтобы, варьируя исходные (входные) параметры процесса, получить требуемые конечные (выходные) параметры структур. Технологическое моделирование позволяет предсказать результаты технологического процесса и определить оптимальные условия и режимы его проведения, не осуществляя дорогостоящих экспериментов, экономя время, энергию и материалы.

5.1. Ионная имплантация

Обычно для описания профиля распределения имплантированной примеси в мишени пользуются симметричной функцией Гаусса двух параметров – среднего проецированного пробега R_р и среднеквадратичного разброса (страг­глинга) проецированных пробегов ΔR_р:

где Q – количество внедренной примеси, или доза имплантации, ион/см².

Реальные распределения имплантированной примеси как в кристаллической, так и в аморфной мишенях несимметричны относительно R_р и описываются функцией Пирсона f(x) четырех параметров: пробега R_р, страгглинга ΔR_р, ассиметрии G(SK) и затухания B [6], [8]:

(5.1)

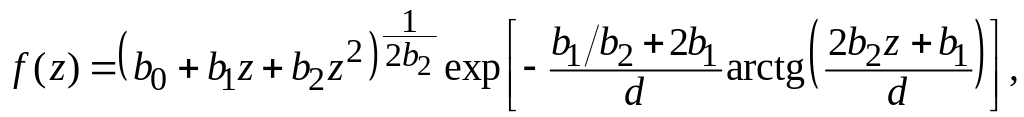
где

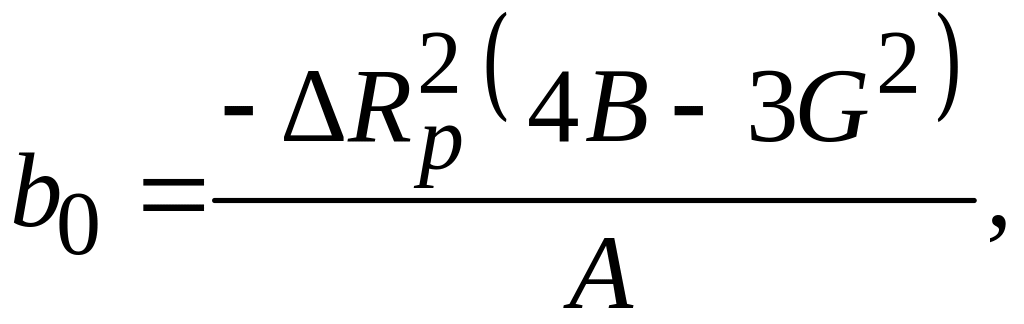
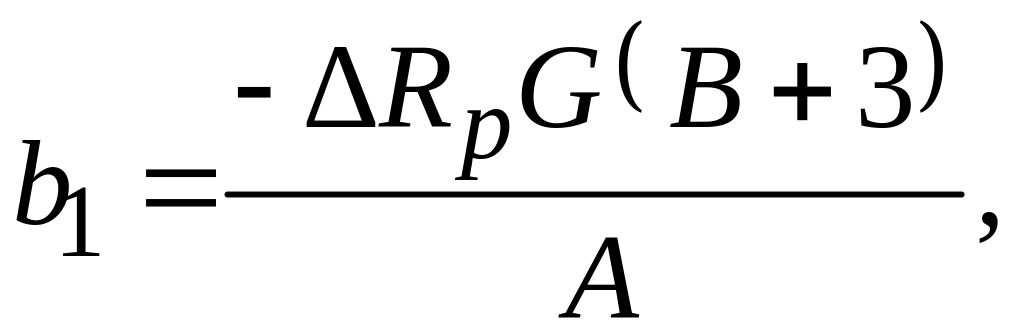
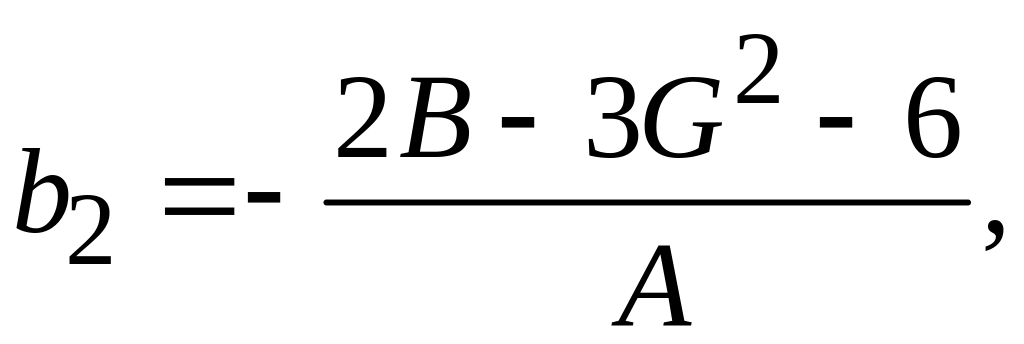
Параметры B и G связаны друг с другом соотношением

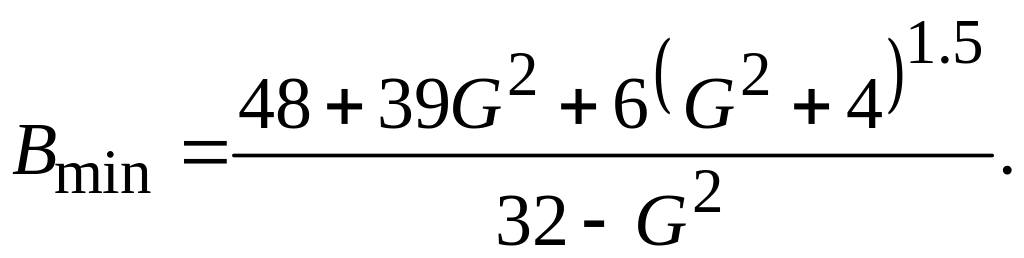
Для легких и средних ионов (бор, фосфор) принимается B = 1.5B_min, а для тяжелых ионов (мышьяк, сурьма) B = B_min. Нормировочный коэффициент (K) в (5.1) находится из условия

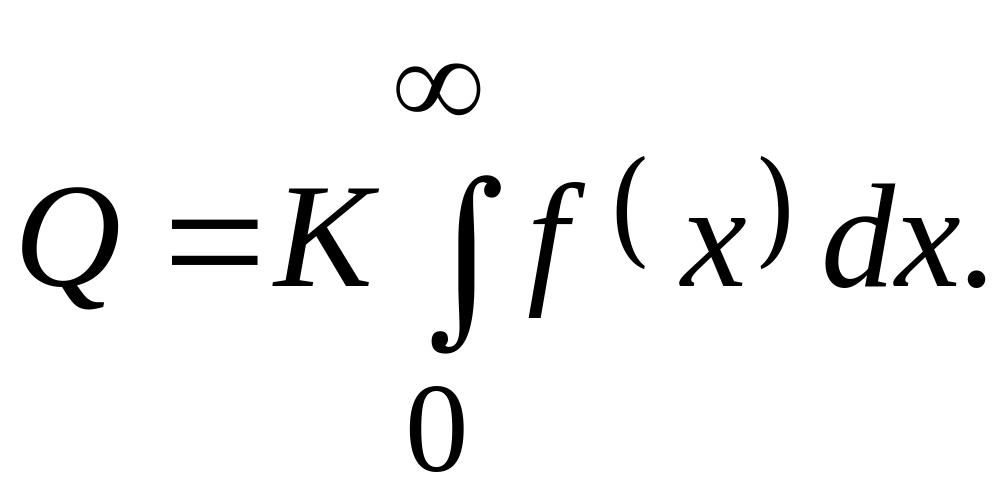(5.2)

Поскольку при x > R_р функция Пирсона является сильно убывающей, в качестве верхнего предела интегрирования в (5.2) можно взять толщину подложки (H) или принять H ≈ 10R_р.

Параметры распределения Пирсона для различных ионов и мишеней в зависимости от энергии имплантации приведены в таблицах [9]. Для основных легирующих примесей в кремнии (B, P, As, Sb) и мишеней Si и SiO₂ эти параметры приведены в прил. 1, 2.

5.2. Ионная имплантация через пленку

Возможность внедрения примеси в подложку через нанесенную на ее поверхность пленку другого материала является одним из достоинств ионной имплантации и часто используется в технологии ИМС, например при подлегировании канала МОП-транзистора через подзатворный оксид. Для определения распределений имплантированной примеси в такой двуслойной системе используется следующий алгоритм:

1) определяются параметры распределения Пирсона для мишени из материала пленки;

2) рассчитывается нормировочный коэффициент из условия

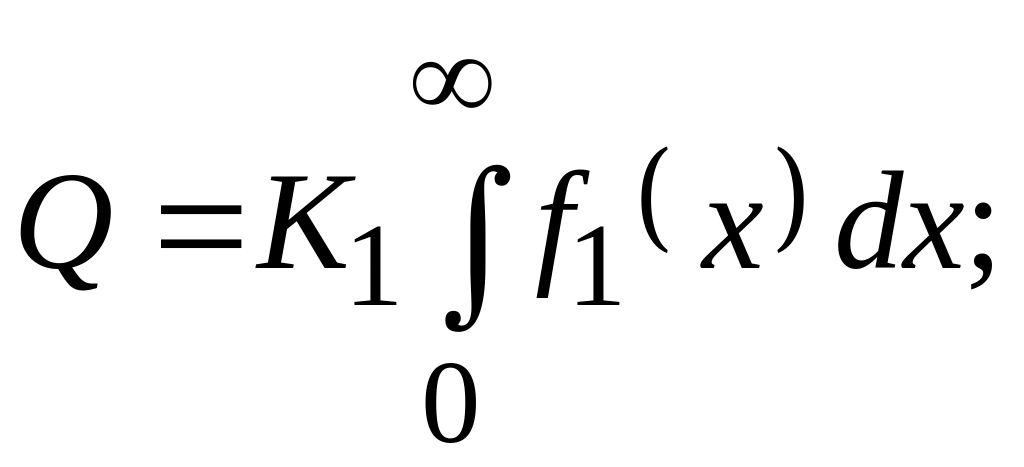
3) рассчитывается количество примеси в пленке толщиной h:

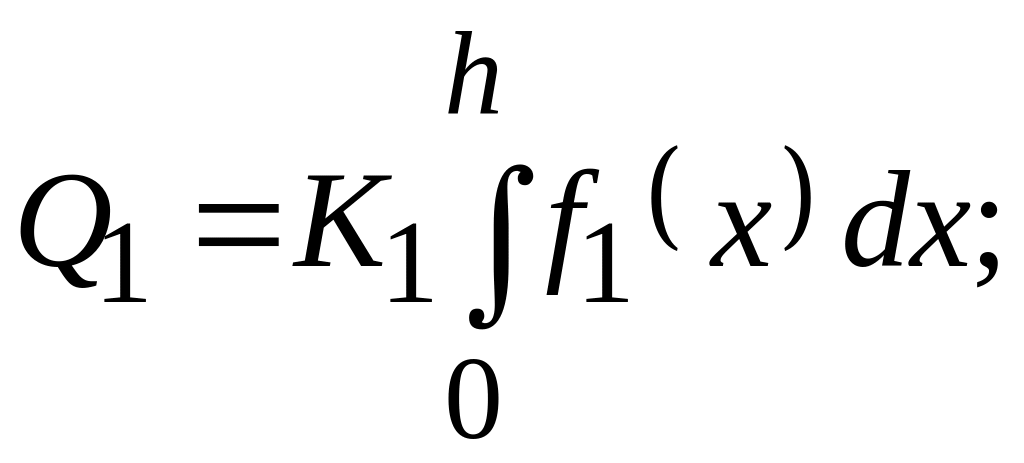
4) определяются параметры распределения Пирсона для мишени из материала подложки;

5) рассчитывается нормировочный коэффициент из условия

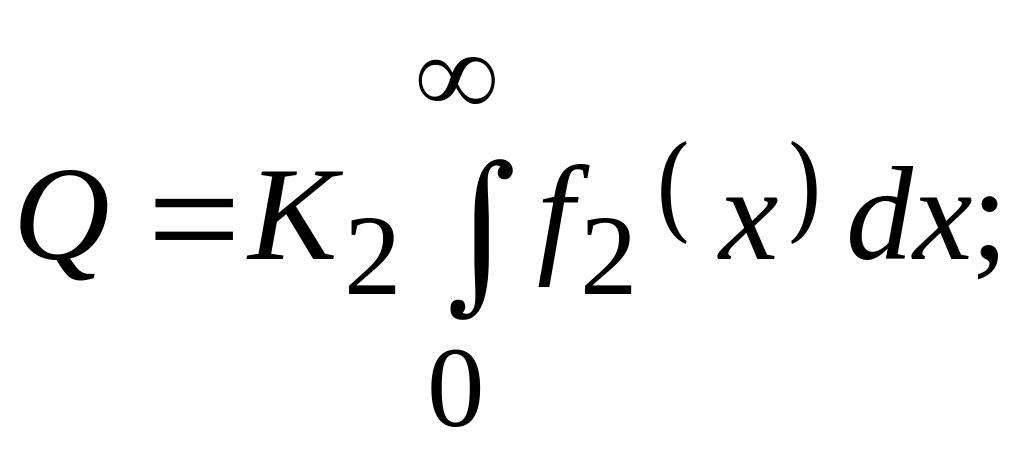(5.3)

6) определяется эффективная толщина пленки h*, содержащая количество примеси , из условия

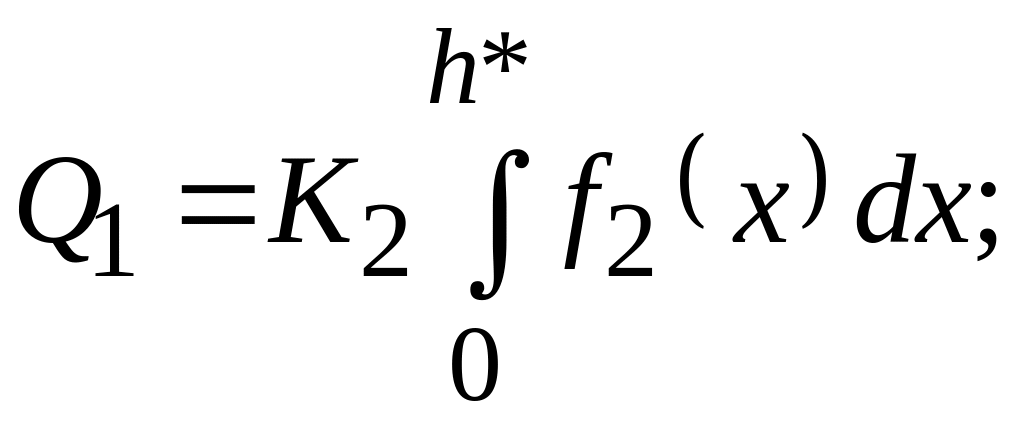(5.4)

7) рассчитывается распределение имплантированной примеси:

– в подложке при x  h:

– пленке при x ≤ h:

При разных параметрах распределения Пирсона в пленке и подложке на границе раздела при х = h имеет место скачок концентрации, т. е. С₁(h) ≠ ≠ С₂(h). Точность определения h* из условия (5.3) определяется шагом интегрирования. В качестве верхних пределов интегрирования в (5.3) и (5.4) можно брать толщину подложки (H) или принять H ≈ 10R_р.