10

Эконометрика Контрольная работа Вариант a

4. Моделирование временных рядов.

Имеются поквартальные условные данные об объемах потребления электроэнергии жителями региона.

Таблица 4.1

Номер квартала	Потребление электроэнергии жителями региона, млн. кВтч	Номер квартала	Товарооборот % к предыдущему периоду
1	6,0	9	8,0
2	4,4	10	5,6
3	5,0	11	6,4
4	9,0	12	11,0
5	7,2	13	9,0
6	4,8	14	6,6
7	6,0	15	7,0
8	10,0	16	10,8

Задания:

1. Постройте автокорреляционную функцию временного ряда. Охарактеризуйте структуру этого ряда.

2. Рассчитайте сезонную компоненты временного ряда и постройте его аддитивную и мультипликативную модели.

3. Рассчитайте трендовую компоненту временного ряда. Постройте графики построенных рядов.

4. Оцените качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение

1. При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называютавтокорреляцией уровней ряда.Количественно ее можно измерить с помощью коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутых на несколько шагов во времени. Число уровней, по которым рассчитывается коэффициент автокорреляции, называетсялагом. Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называетсяавтокорреляционной функциейвременного ряда. Анализ автокорреляционной функции позволяет выявить структуру временного ряда.

Для расчета коэффициентов автокорреляции исходного временного ряда составим таблицу (табл. 4.2):

Таблица 4.2

t	yt	yt-1	yt-2	yt-3	yt-4	yt-5	yt-6
1	6,0	–	–	–	–	–	–
2	4,4	6,0	–	–	–	–	–
3	5,0	4,4	6,0	–	–	–	–
4	9,0	5,0	4,4	6,0	–	–	–
5	7,2	9,0	5,0	4,4	6,0	–	–
6	4,8	7,2	9,0	5,0	4,4	6,0	–
7	6,0	4,8	7,2	9,0	5,0	4,4	6,0
8	10,0	6,0	4,8	7,2	9,0	5,0	4,4
9	8,0	10,0	6,0	4,8	7,2	9,0	5,0
10	5,6	8,0	10,0	6,0	4,8	7,2	9,0
11	6,4	5,6	8,0	10,0	6,0	4,8	7,2
12	11,0	6,4	5,6	8,0	10,0	6,0	4,8
13	9,0	11,0	6,4	5,6	8,0	10,0	6,0
14	6,6	9,0	11,0	6,4	5,6	8,0	10,0
15	7,0	6,6	9,0	11,0	6,4	5,6	8,0
16	10,8	7,0	6,6	9,0	11,0	6,4	5,6

Определим коэффициент корреляции между рядами y_tиy_t-1, т.е. коэффициент автокорреляции 1-го порядка

, (4.1)

где

, .

Отметим, что расчет коэффициента автокорреляции производится по 15, а не по 16 парам наблюдений.

Составим таблицу для расчета коэффициента автокорреляции 1-го порядка (таб. 4.3):

Таблица 4.3

t	yt	yt-1
1	6,0	–	–	–	–	–	–
2	4,4	6,0	-2,987	-1,067	3,186	8,920	1,138
3	5,0	4,4	-2,387	-2,667	6,364	5,696	7,111
4	9,0	5,0	1,613	-2,067	-3,334	2,603	4,271
5	7,2	9,0	-0,187	1,933	-0,361	0,035	3,738
6	4,8	7,2	-2,587	0,133	-0,345	6,691	0,018
7	6,0	4,8	-1,387	-2,267	3,143	1,923	5,138
8	10,0	6,0	2,613	-1,067	-2,788	6,830	1,138
9	8,0	10,0	0,613	2,933	1,799	0,376	8,604
10	5,6	8,0	-1,787	0,933	-1,668	3,192	0,871
11	6,4	5,6	-0,987	-1,467	1,447	0,974	2,151
12	11,0	6,4	3,613	-0,667	-2,409	13,056	0,444
13	9,0	11,0	1,613	3,933	6,346	2,603	15,471
14	6,6	9,0	-0,787	1,933	-1,521	0,619	3,738
15	7,0	6,6	-0,387	-0,467	0,180	0,150	0,218
16	10,8	7,0	3,413	-0,067	-0,228	11,651	0,004
	110,8	106			9,813	65,317	54,053

По данным таблицы находим

, .

Используя формулу (3.1), находим

.

Определим теперь коэффициент автокорреляции 2-го порядка, коэффициент корреляции между рядами y_tиy_t-2, т.е.

, (4.2)

где

, .

Отметим, что расчет коэффициента автокорреляции 2-го порядка уже будет производится по 14 парам наблюдений.

Составим таблицу для расчета коэффициента автокорреляции 2-го порядка (таб. 4.3):

Таблица 4.4

t	yt	yt-2
1	6,0	–	–	–	–	–	–
2	4,4	–	–	–	–	–	–
3	5,0	6,0	-2,600	-1,071	2,786	6,760	1,148
4	9,0	4,4	1,400	-2,671	-3,740	1,960	7,137
5	7,2	5,0	-0,400	-2,071	0,829	0,160	4,291
6	4,8	9,0	-2,800	1,929	-5,400	7,840	3,719
7	6,0	7,2	-1,600	0,129	-0,206	2,560	0,017
8	10,0	4,8	2,400	-2,271	-5,451	5,760	5,159
9	8,0	6,0	0,400	-1,071	-0,429	0,160	1,148
10	5,6	10,0	-2,000	2,929	-5,857	4,000	8,577
11	6,4	8,0	-1,200	0,929	-1,114	1,440	0,862
12	11,0	5,6	3,400	-1,471	-5,003	11,560	2,165
13	9,0	6,4	1,400	-0,671	-0,940	1,960	0,451
14	6,6	11,0	-1,000	3,929	-3,929	1,000	15,434
15	7,0	9,0	-0,600	1,929	-1,157	0,360	3,719
16	10,8	6,6	3,200	-0,471	-1,509	10,240	0,222
	106,4	99			-31,120	55,760	54,049

По данным таблицы находим

, .

Используя формулу (3.2), находим

.

Аналогичным образом рассчитываем коэффициенты автокорреляции 3-го и более высоких порядков. (Заметим, что в программе Exelкоэффициенты корреляции рассчитываются при помощи функции КОРРЕЛ). В результате получим автокорреляционную функцию исходного временного ряда. Ее значения и коррелограмма приведены в таб. 3.5.

Таблица 4.5

Лаг	Коэффициент автокорреляции уровней временного ряда	Коррелограмма
1	0,1651548
2	-0,5668734
3	0,1135581
4	0,9830252
5	0,1187113
6	-0,7220463
7	-0,0033676
8	0,9738481

Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции,во-вторых, сезонных колебаний периодичностью в четыре квартала. Данный вывод подтверждается и графическим анализом структуры ряда (см. рис. 4.1).

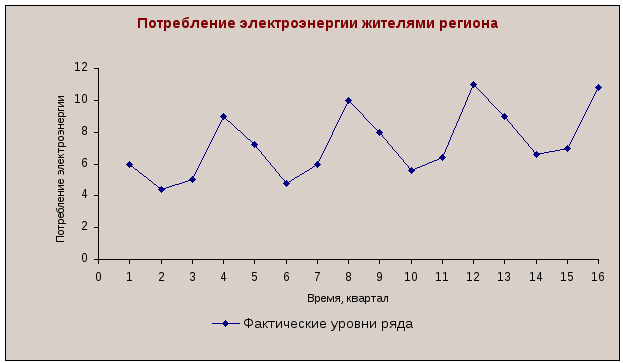
Рис. 4.1