8 семестр, вечерка, Шануренко / Типовой расчет системы охлаждения / Расчет принудительного водяного охлаждения мощных электронных приборов

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА ЭЛЕКТРОННЫХ ПРИБОРОВ

ТИПОВОЙ РАСЧЕТ

Тема: Расчет принудительного водяного охлаждения мощных электронных приборов

Студент гр. 9802 _________________________ Попов А. П.

Преподаватель _________________________ Шануренко А. К.

Санкт-Петербург

2023

ВВЕДЕНИЕ

Принудительное водяное охлаждение нашло самое широкое распространение в практике эксплуатации электровакуумных приборов большой мощности. В качестве теплоносителя используется очищенная и обессоленная вода, которая при помощи распределительных устройств подается под давлением в каналы охлаждения прибора с расчетной скоростью.

Задача охлаждения тепловыделяющего элемента, в частности анода лампы, состоит в определении конструкции его охлаждаемой поверхности и в выборе параметров потока охлаждающей воды. Специфика работы мощных электронных ламп состоит в высокой тепловой нагруженности их электродов, в ряде случаев превышающей нагрузки на активные поверхности ядерных реакторов. Удельные тепловые нагрузки на анодах ламп вещательного диапазона достигают 150 ·10⁴ Вт/м², а у СВЧ-приборов с се-точным управлением до (300…500)10⁴ Вт/м².

Если температура охлаждаемой поверхности не превышает температуру кипения воды t_s при рабочем давлении, имеет место чисто конвективный режим охлаждения. Например, при давлении p = 2 бар температура кипения воды составляет 120 °С.

Режим конвективного охлаждения может быть реализован при относительно низких тепловых потоках (менее 20 ·10⁴ Вт/м²). В конвектив-ном режиме охлаждения перегрев охлаждаемой стенки относительно температуры воды в соответствии с законом Ньютона пропорционален удельному тепловому потоку q: q = α_k (t – t_в) Вт/м², где α_k – конвективный коэффициент теплоотдачи, Вт/(м²·°С).

Коэффициент теплоотдачи α_k характеризует интенсивность теплообмена между твердой стенкой и водяным потоком и является величиной, обратной удельному тепловому сопротивлению на границе "стенка–жидкость". Природа возникновения этого теплового сопротивления связана с тормозящим действием сил вязкости, приводящих к образованию у поверхности динамического пограничного слоя жидкости, на котором происходит падение скорости воды от среднего значения в потоке до нуля на стенке (прилипание).

В условиях нагрева на охлаждаемой поверхности формируется и тепловой пограничный слой, на котором происходит изменение температуры от нагретой стенки до температуры потока. Толщины динамического и теплового пограничных слоев на противоположных поверхностях канала увеличиваются по длине канала до полного их смыкания. Расстояние от входа до точки смыкания слоев называется участком динамической и тепловой стабилизации. Отсюда следует, что, чем короче канал, тем тоньше тепловой и динамический слои, тем выше теплоотдача. Подобие теплового и гидродинамического полей в пограничном слое определяется безразмерным критерием Прандтля (Pr), который является физическим параметром вещества, так как составлен как отношение двух физических параметров – кинематической вязкости ν и температуропроводности a.

Коэффициент температуропроводности a выражается в тех же единицах измерения, что и кинематическая вязкость ν [м²/с] и является мерой теплоинерционных свойств материала Pr = ν/a.

Для капельных жидкостей, к которым относится и вода, критерий Прандтля Pr >> 1. По этой причине существенное влияние на теплоотдачу при водяном охлаждении играет гидродинамика процесса, определяемая скоростью жидкости, формой и длиной канала, вязкостью жидкости.

Величиной, характеризующей гидродинамический режим течения, является безразмерный критерий Рейнольдса, который можно интерпретировать как отношение сил инерции к силам вязкости:

Re = ωd_экв/ ν,

где ω – скорость жидкости в канале, м/с; d_экв = 4S/П – эквивалентный диаметр канала (отношение учетверенного сечения канала к его периметру), м; ν – кинематическая вязкость жидкости, м²/с.

Для практических расчетов коэффициента теплоотдачи используются полуэмпирические зависимости между безразмерным коэффициентом теплоотдачи – критерием Нуссельта (Nu) и критериями Рейнольдса и Прандтля

Nu = (α_k d_экв)/λ_в = f(Re, Pr),

где λ_в – теплопроводность воды, Вт/(м · °С).

При малых числах Re (Re < 2200) движение жидкости имеет устойчивый упорядоченный слоистый характер, называемый ламинарным. В ламинарном режиме теплопередача через пограничный слой происходит в основном за счет молекулярной теплопроводности. Рекомендуемая формула для расчета теплоотдачи в этом режиме имеет вид

Nu = 1,85 ( Re · Pr · d_экв/l)^1/3,

где l – длина канала.

При Re > 2200 устойчивость потока нарушается, движение жидкости приобретает качественно новый, неупорядоченный (турбулентный) характер, пульсации скорости глубже проникают в пограничный слой, что вызывает перемешивание больших масс жидкости. Но и при турбулентном режиме течения вблизи твердой стенки сохраняется очень тонкий пограничный слой, который и ограничивает теплопередачу.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Расчет водяной системы охлаждения

Зададим начальные условия в соответствии с расчетом геометрии ВТКК и методическим указаниям и рассчитаем геометрию и характеристики водяной системы охлаждения.

Критерий Нуссельта (Nu) характеризует отношение плотности теплового потока конвективной теплоотдачей к плотности теплового потока кондукцией в слое текучей среды вблизи стенки. Критерий Нуссельта – безразмерная величина.

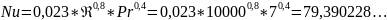
Величиной, характеризующей гидродинамический режим течения, является безразмерный критерий Рейнольдса, который можно интерпретировать как отношение сил инерции к силам вязкости:

По методическим указаниям, Re = 10000…15 000. Задано Re = 10000.

Для капельных жидкостей, к которым относится и вода, критерий Прандтля Pr >> 1. По методическим указаниям, Pr = 7.

Коэффициент теплоотдачи

где d_экв – эквивалентный диаметр трубопровода. Приближенно может быть принят равным удвоенной величине зазора между стенками анода и бака, т.е. d_эф = 2δ = D_{a нар} – D_б (D_{a нар}, D_б ‒ наружный диаметр анода и внутренний диаметр бака соответственно); λ_в = 0,608 Вт/(м ·°С) – теплопроводность воды; δ ‒ 2…4 мм.

Наружная температура анода

;

где P_a – рассеиваемая мощность анода; P­_н – рассеиваемая мощность накала; P_c – рассеиваемая мощность сетки; L_a = l ‒ протяженность анода; D_{a нар} - наружный диаметр анода; t₀ = средняя температура воды в баке.

В соответствии с расчетом триода:

L_a = 92 мм; D_{a нар} = 70 мм; мощность накала катода P_Н = 436,36 Вт.

Зададим .

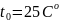ξ = 0,9; θ = 60^о из расчета динамического режима работы.

,

где S – крутизна анодно-сеточной характеристики прибора по управляющей сетке и напряжения на электродах в точке, соответствующей I_{а max}, D – проницаемость управляющей сетки. Обе величины – константы из расчета геометрии ВТКК.

;

; ;

; (из расчета динамического режима работы);

.

; Вт.

Коэффициенты разложения в ряд Фурье косинусоидального аппроксимирующего импульса анодного тока α₀ и α₁

;

;

.

.

;

;

;

;

;

.

.

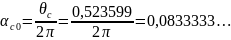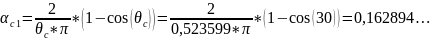, где P₀ – мощность, отбираемая от источника постоянного напряжения на аноде, P_вых – выходная мощность

_.

_, где – ток эмиссии, H – эффективность.

.

Скорость потока воды

.

Расход воды

.

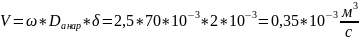Нагрев выходящей воды

.

Температура жидкости на выходе

t _вых = .

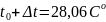10