14.Вывод расчетных формул для наружной токоподводящей трубки
На
рис. 4.9 приведен эскиз наружной
токоподводящей трубки. Введем
следующие обозначения: δн
– толщина трубки, м; λн
– теплопроводность трубки, Вт/(м·
°С);
ρн
– удельное электрическое сопротивление,
Ом·м; ξ – координата, где происходит
переход от одной аппроксимирующей
зависи-мости к другой; t(L)
– температура вывода; t1(0)
– температура (макси-мальная) начала
трубки; J
– ток на-кала, А; ∆t
= [t
–
t(L)]
= Т
–
теку-щая температура трубки относительно
температуры оболочки; dн
– наруж-ный диаметр трубки.
О
x
Рис.
4.9
На начальном, горячем участке трубки 0 < х < ξ, где перегрев трубки превышает 600°С, стоки тепла за счет лучеиспускания приведенные к единице объема трубки
Коэффициент теплопроводности λн и удельное сопротивление ρн молибдена слабо зависят от температуры. Поэтому были приняты их средние значения. С учетом введенных обозначений, дифференциальное уравнение теплопроводности имеет вид
,
0 < х <
ξ (4.2)
Обозначим
;
;
Тогда уравнение (4.2) можно записать в следующем виде
(4.3)
Решение уравнения (4.3)
при
x
= 0:
;
при
x
= ξ:
;
;
.
Обозначим
;
.
Пока неизвестна ни координата ξ ни постоянная В.
Для второго участка поместим начало координат в точку х = ξ, тогда конец трубки (вывод) будет иметь координату (L – ξ).
Уравнение для второго участка: 0 < x < (L – ξ);
;
.
Обозначим
.
Тогда
.
(4.4)
Решение уравнения (4.4):
При 0 < x < (L – ξ);
.
При x = (L – ξ) – конец трубки:
,
или
Используем условие равенства тепловых потоков в точке х = ξ для первой области и при х = 0 для второй, так как это одна и та же точка:
.
После нахождения производных и решения алгебраического уравнения:
.
В итоге для нахождения координаты ξ необходимо решить следующее трансцендентное уравнение:
.
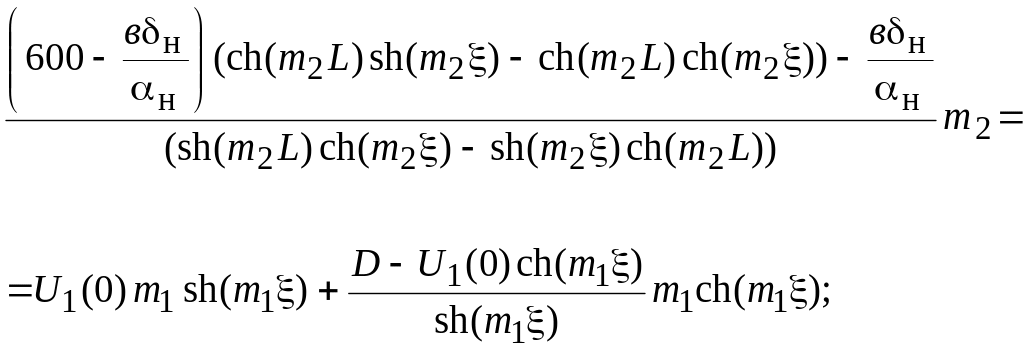
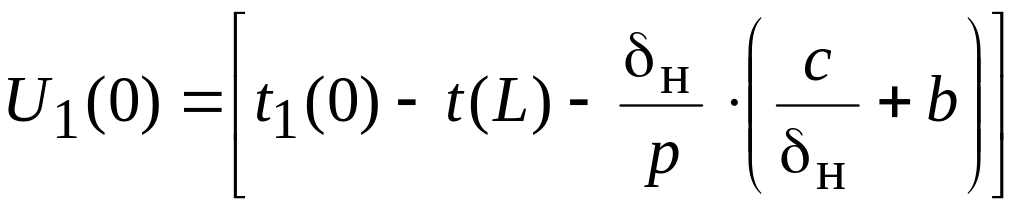Координата ξ зависит от температуры начала трубки t1(0). Чем выше эта температура, тем больше величина ξ, иначе говоря, чем горячее трубка, тем дальше простирается область действия второй аппроксимирующей линии. Вычислив ξ, можно для любой начальной температуры t1(0) найти зависимости для вычисления температуры по всей длине трубки (семейство кривых).
Из полученного семейства выбирается только та кривая, у которой выполняется условие равенства тепловых потоков через трубку и чашку в месте их присоединения, т. е.
,
где fu = 2πr1δ – cечение чашки в месте присоединения к трубке; fтр = πdтрδтр – сечение трубки.
Уравнение теплопроводности для чашки (рис. 4.10) в цилиндрических координатах имеет вид
,
где
–
параметр, определяющий джоулевое
тепловыделение в чашке.
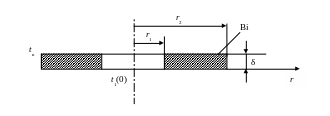
Рис. 4.10
Тепловое
взаимодействие между чашками и нитями
накала характеризуется безразмерным
коэффициентом, критерием Био (Bi),
определяемым как
,
где α – коэффициент теплопередачи
между нитями и чашкой, Вт/(м2·
°С).
Коэффициент теплопередачи может быть вычислен, если известна длина охлажденного участка катода L0:
,
где λв – теплопроводность вольфрама, Вт/(м· °С).
При длине охлажденного участка L0 = 10·10–3 м, и теплопроводности вольфрама λв = 100 Вт/(м· °С)
Величина а при токе накала 370 А
Решение уравнения для диска
.
Тепловой поток в месте присоединения чашки к трубке
Варианты расчетов:
1. температура начала наружной трубки t1(0) = 1200 °C:
0 < x < ξ = 0.06, m1 = 23.166;
,
ξ = 0.06, 0 < x < 0.119 (0.179).
Распределение температур:
-
(x – ξ)
x = 0
1200 °C
t1
–
0.01
1118
–
0.02
1050
–
0.03
992
–
0.04
941
–
0.05
895
(0)
0.06
850
t2
(0.01)
0.07
805
(0.02)
0.08
760
(0.04)
0.10
670
(0.06)
0.12
575
(0.08)
0.14
473
(0.1)
0.16
364
(0.119)
0.179
250
Тепловой поток через начало трубки Р(0) = 98,6 Вт.
Тепловой поток через вывод Р(L) = 69,0 Вт.
2. Температура начала наружной трубки t1(0) = 1100 °C:
0 < x < ξ = 0.051;
ξ = 0.051, 0 < x < 0.128 (0.179), m2 = 7.45.
Распределение температур:
-
(x – ξ)
x = 0
1100 °C
t1
–
0.01
1037
–
0.02
984
–
0.03
937
–
0.04
894
(0)
0.051
850
t2
(0.009)
0.06
813
(0.019)
0.07
773
(0.029)
0.08
732
(0.039)
0.09
690
(0.049)
0.10
647
(0.069)
0.12
559
(0.089)
0.14
463
(0.109)
0.16
360
(0.128)
0.179
250
Тепловой поток через начало трубки Р(0) = 74,9 Вт.
Тепловой поток через вывод Р(L) = 65,7 Вт.
3. температура начала наружной трубки t1(0) = 1000 °C.
0 < x < ξ = 0.038;
,
ξ = 0.038, 0 < x < 0.141 (0.179), m1= 23.166, m2 = 7.45.
Распределение температур:
-
(x – ξ)
x = 0
1000 °C
t1
–
0.01
954
–
0.02
915
(0)
0.038
850
t2
(0.012)
0.05
808
(0.022)
0.06
772
(0.042)
0.08
698
(0.062)
0.10
621
(0.082)
0.12
539
(0.102)
0.14
450
(0.122)
0.16
353
(0.141)
0.179
250
Тепловой поток через начало трубки Р(0) = 52,5 Вт.
Тепловой поток через вывод Р(L) = 62,4 Вт.
4. Температура начала наружной трубки t1(0) = 950 °C.
0 < x < ξ = 0.029;
ξ = 0.029, 0 < x < 0.15 (0.179).
Распределение температур:
-
(x – ξ)
x = 0
950 °C
t1
–
0.01
913
–
0.02
880
(0)
0.029
850
t2
(0.011)
0.04
814
(0.021)
0.05
781
(0.031)
0.06
748
(0.051)
0.08
679
(0.071)
0.10
607
(0.091)
0.12
528
(0.111)
0.14
444
(0.131)
0.16
350
(0.15)
0.179
250
Тепловой поток через начало трубки Р(0) = 42.2 Вт.
Тепловой поток через вывод Р(L) = 60.4 Вт.
Тепловой поток через чашку в месте соединения с трубкой Р(r1) = 44 Вт, что близко к Р(0). Поэтому из всего семейства кривых выбираем последнюю.