СВЧ 7 семестр Вьюгинов / Доклады / Общие свойства медленных волн. Теорема Флоке

Общие свойства медленных волн. Теорема Флоке

Медленные волны применяются в электронике СВЧ и ускорительной технике для осуществления длительного взаимодействия электромагнитного поля с потоком заряженных частиц. Это взаимодействие используется в ряде приборов (как, например, клистрон, лампа с бегущей волной, многокамерный магнетрон, усилитель с двумя пучками, магнетронный усилитель и др.) для возбуждения и усиления электромагнитных колебаний сверхвысоких частот.

Рассмотрим механизм использования медленных волн. Важную роль в этом взаимодействии играет эффект Черенкова, состоящий в том, что заряжённая частица, равномерно движущаяся в системе, в которой могут распространяться медленные волны, сама способна излучать такие волны, если только её скорость превосходит некоторое критическое значение. При этом излучение имеет место независимо от того, движется ли частица в диэлектрике или в вакууме.

Если с медленными волнами взаимодействует не отдельная частица, а немодулированный пучок заряжённых частиц с достаточно малой плотностью, причём скорость пучка превосходит критическое значение скорости в эффекте Черенкова, то состояние пучка становится неустойчивым и имеющиеся в нём флуктуации плотности распространяются в виде волн плотности заряда с нарастающей амплитудой. Такой же характер имеют возбуждающиеся при этом медленные электромагнитные волны. Неустойчивость пучка и возникновение волн с нарастающей амплитудой играют существенную роль в механизме возбуждения и усиления колебаний сверхвысоких частот во всех приборах, где используется взаимодействие электронного пучка с медленными волнами (например, в указанных ранее приборах).

Такое взаимодействие возникает, если заряженные частицы и электромагнитная волна движутся с приблизительно одинаковыми скоростями. Так как скорость частиц не может превышать скорость света, для реализации длительного взаимодействия необходимо замедлить электромагнитные волны. Использовать диэлектрические волноводы при этом нецелесообразно, из-за больших потерь. Помимо этого, не все диэлектрики можно поместить в вакуум, в котором движутся заряженные частицы. Поэтому для создания медленных волн разработаны специальные металлические и металлодиэлектрические линии передачи, называемые замедляющими системами.

Для выяснения принципов построения ЗС рассмотрим условия существования и основные свойства медленных волн. Не вдаваясь в подробности других тем и выкладок математической физики, тезисно можно сказать, что для существования медленных незатухающих электрических волн необходимо, чтобы на поверхности ЗС (или её части) продольное поверхностное сопротивление Z_s||=E_z/H_l было отлично от нуля и имело индуктивных характер. Аналогично, для существования медленных магнитных волн поверхность ЗС должна обладать емкостным поперечным поверхностным сопротивлением Z_s=iX_s. Если образующие ЗС тела имеют как продольное, так и поперечное поверхностное сопротивление, в ней распространяются гибридные медленные волны. Поверхности, обладающие ненулевыми сопротивлениями Z_s, называют импендансными. Напряженность поля медленной волны уменьшается по мере удаления от таких поверхностей. Скорость убывания поля увеличивается с ростом поперечного волнового числа τ и, с увеличением частоты и замедления поле сильнее «прижимается» к импендансным поверхностям.

Пример.

Рассмотрим плоскую поверхность x=0, над которой в направлении оси z распространяется медленная E-волна. Её электромагнитное поле определяется мембранной функцией

ψ= e^-τx‑. (считаем, что волна однородна (совпадают плоскости амплитуд и фаз) по координате y). , где τ – связь замедления фазовой скорости с поперечным волновым числом. n_ф = β/k = ; τ=k .

Составляющие электромагнитного поля вычислим по формулам, полученным решением уравнения Максвелла в линии передачи (формулы 6.1, 6.2)

_x = iβτ e^-τxe^-iβz;

_z = -τ² e^-τxe^-iβz;

_y = iωετ e^-τxe^-iβz;

Зависимость продольной составляющей электрического поля этой волны от нормированного расстояния до имендансной плоскости показана на рисунке

Рис. 1. Распределение поля медленной волны в поперечном сечении линии передачи.

Как следует из этих выражений, плоскость, направляющая волну, должна обладать продольным поверхностным сопротивлением

Z_s||=iX_s|| = _z(0)/ _y(0) = iZ₀ что согласуется со сделанным ранее выводом.

Замедление, соответствующее данному значению поверхностного сопротивления, можно вычислить по формуле

= [( )²+1]^1/2.

Характеристическое сопротивление E-волны

=E_x/H_y=Z₀β/k=Z₀n_Ф.

В n_Ф раз больше, чем T-волны. При больших замедлениях амплитуда напряженности магнитного поля уменьшается настолько, что её при расчете электрического поля можно пренебречь и вычислять последнее методами квазистатики.

Поверхностное сопротивление гладкого металлического проводника в СВЧ-диапазона практически равно нулю. Поэтому в линии передачи, образованной такими проводниками, распространение медленных волн невозможно. Для создания замедляющих систем используются гофрированные (ребристые) металлические поверхности.

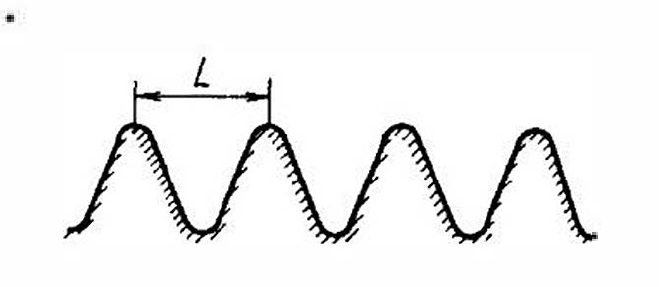
Рис. 2. Гофрированные металлические поверхности

На уровне вершин гофра среднее значение продольной составляющей электрического поля отлично от нуля. Если длина замедленной полны λ_g много больше расстояния между выступами гофра L, то волна как бы «не чувствует» отдельных выступов и впадин (неоднородностей) гофрированной структуры, как вдоль гладкой имендансной поверхности. Это называется условием малости. Если оно не выполняется, то гофрированную поверхность необходимо рассматривать как периодическую структуру.

Общие закономерности распространения вол в периодических структурах определяются теоремой Флоке:

Для данного типа волны электромагнитные поля в поперечных сечениях периодической структуры, отстоящих друг от друга на период, отличаются только фазовым множителем.

(x₁, x₂, z+L) = (x₁, x₂, z) e^-iφ;

(x₁, x₂, z+L) = (x₁, x₂, z) e^-iφ,

Где x₁, x₂ – координаты точки поперечного сечения; L – период структуры, равный минимальному расстоянию, при перемещении на которое она совмещается сама с собой, – сдвиг фазы в сечениях, отстоящих друг от друга на один период.

В общем случае = - ’’ – комплексная величина, причем действительная её часть определяет сдвиг фазы поля в периодической структуре, а мнимая – изменение его амплитуды. Согласно теореме Флоке, все возможные значения угла лежат в интервале [-π; π], так как функция e^-iφ имеет период 2π. При положительных значениях угла пол в сечении z+L отстает по фазе от поля в сечении z, что определяет положительное значение фазовой скорости волны. Отрицательным значениям угла соответствует отрицательное значение u_Ф. Поскольку свойства волн с противоположными направлениями фазовых скоростей одинаковы, достаточно рассмотреть значения угла , заключенные в интервале [0; π]