Из учебника с. А. Фридрихова и с. М. Мовнина « физические основы электронной техники», м. 1982

Глава 11

Электрические явления в газах

§ 11.1. Появление и исчезновение заряженных частиц в газе

Появление электрических зарядов в газе. Процесс прохождения электрического тока в газовой среде называется электрическим газовым разрядом. В элементарных явлениях, определяющих прохождение тока в газе, участвуют различные микрочастицы – электроны, положительные и отрицательные ионы, нейтральные атомы и молекулы, а также кванты электромагнитного излучения.

Условия прохождения тока через разрядный промежуток определяются также рядом внешних параметров, таких, как конфигурация, размеры, проводимость, эмиссионные свойства электродов и стенок сосуда с газом, давление и состав газа, частота внешнего поля, сила тока и т.д. Свойства среды, в которой протекает разряд, неизотропны. Все это затрудняет создание строгой и единой теории газового разряда. В значительной мере теория разряда опирается на приближенные расчеты и эмпирические соотношения, хотя для ряда конкретных условий получены количественные закономерности.

Газ – хороший диэлектрик, однако при достаточно больших напряженностях внешних полей его проводимость резко увеличивается за счет повышения концентрации заряженных частиц. Электрические заряды могут появляться в самой газовой среде в результате элементарных актов взаимодействия (столкновений) частиц, а также за счет всех видов эмиссии с электродов и стенок сосуда, в котором протекает разряд. Эмиссия заряженных частиц с поверхности твердых тел была рассмотрена ранее, поэтому остановимся лишь на процессах столкновения частиц в газе, приводящих к возбуждению и ионизации атомов или молекул.

При малых энергиях сталкивающихся частиц возможны лишь упругие столкновения, в результате которых сохраняется неизменной суммарная кинетическая энергия частиц. С увеличением энергии повышается вероятность столкновений, при которых часть кинетической энергии переходит во внутреннюю энергию частиц (неупругое столкновение первого рода). Возможен и обратный переход – суммарная кинетическая энергия сталкивающихся частиц увеличивается за счет их внутренней энергии (неупругое столкновение второго рода). В процессе неупругого столкновения атом перейдет в возбужденное состояние, если его внутренняя энергия увеличилась не менее чем на eV₁, где V₁ – первый потенциал возбуждения атома. Если же переданная атому энергия превышает энергию ионизации eV_i (V_i – потенциал ионизации), то один из валентных электронов может быть удален из атома с образованием положительного иона. Наряду с однозарядными ионами при достаточной величине полученной энергии могут образоваться многократно заряженные ионы. Вероятность актов возбуждения или ионизации характеризуется так называемым эффективным сечением.

Понятия эффективных сечений рассматриваются в кинетической теории газов, где определяется вероятность различных видов взаимодействия частиц.

Если поток частиц с концентрацией n проходит сквозь слой газа единичного сечения, то в результате актов взаимодействия, приводящих к рассеянию частиц потока, их концентрация на пути dx уменьшится на величину | dn |, пропорциональную n, dx и концентрации атомов газа N₀ :

(11.1)

Знак «минус» означает уменьшение концентрации потока на участке dx. Коэффициент пропорциональности σ называют эффективным сечением взаимодействия для одной частицы.

Интегрирование выражения (11.1) дает закон уменьшения концентрации частиц потока за счет актов взаимодействия в газовой среде. Если σ и N₀ не зависят от x, то

, (11.2)

где n₀ – начальная концентрация (при x = 0).

Величина Q = σ N₀ представляет собой эффективное сечение взаимодействия на единицу объема. Здесь σ имеет размерность площади, Q – размерность обратной длины. Выражение Q = σ N₀ свидетельствует о том, что можно пренебречь перекрытием сечений отдельных атомов газа и считать суммарное эффективное сечение взаимодействия в единице объема равным сумме эффективных сечений атомов газа в этом объеме .

Если обозначить среднее расстояние, проходимое частицей между двумя актами взаимодействия (среднюю длину свободного пробега), через Λ, то

, (11.3)

а следовательно,

, (11.4)

т.е. Q определяет среднее число актов взаимодействия, которые испытает частица на единице своего пути.

При наличии нескольких различных типов взаимодействия в газовой среде с учетом равенства dx = υdt изменение концентрации потока можно описать выражением

, (11.5)

где индексы k и l относятся соответственно к падающим и рассеивающим частицам; σ_kl – эффективное сечение взаимодействия между частицами сортов k и l.

Поскольку скорости частиц в газе неодинаковы, необходимо усреднить произведение σ_klυ_k по всем скоростям.

Рассмотрим моноэнергетический поток электронов, рассеивающийся в газовой среде, атомы или молекулы которой будем считать неподвижными. Выход электронов из потока обусловлен различными причинами, в частности упругими и неупругими столкновениями, рекомбинацией и т.д. Для характеристики каждого из этих процессов может быть введено соответствующее эффективное сечение и, как следует из формулы (11.5), полное (интегральное) эффективное сечение рассеяния электрона

, (11.6)

где σ_l – эффективное сечение для l-го вида рассеяния; N_0l – концентрация рассеивающих центров сорта l.

Вероятность каждого процесса определяется отношением Q_l / Q.

Величина Q_l = σ_l N_0l равна обратной длине свободного пробега электрона для данного типа взаимодействия, а средняя длина свободного пробега электрона

(11.7)

меньше длины свободного пробега для любого типа взаимодействия.

Эффективные сечения упругих столкновений можно достаточно хорошо рассчитать по законам классической физики, тогда как для неупругих столкновений необходим учет квантовомеханических эффектов.

Обратимся прежде всего к упругим столкновениям. Потенциал сил взаимодействия между частицами зависит от расстояния между ними по закону V~r^-n, где n определяется видом и энергией частиц. Для расчета траектории частицы при упругом столкновении следует решить совместно уравнения законов сохранения кинетической энергии (потенциальная энергия при упругом столкновении не изменяется) и импульса. Тогда, зная начальные скорости и прицельный параметр – наименьшее расстояние между начальными траекториями частиц, получим значения их угловых отклонений после столкновения.

Для описания вероятности рассеяния электронов на различные углы вводят понятие дифференциального эффективного сечения рассеяния на угол θ.

Выделим из потока электронов, движущихся относительно атома газа, ту его часть, для которой прицельные параметры начальных траекторий лежат в пределах от b до b+ db. Выделенная часть потока пройдет через кольцевую область с внутренним радиусом b и шириной db, центр которой расположен в месте нахождения атома. Площадь кольца 2πbdb. Электроны, отклонившись в результате взаимодействия с атомом на угол θ, проходят через телесный угол dΩ = 2πsinθdθ с углом раствора θ.

По определению дифференциальное эффективное сечение σ(υ,θ), умноженное на dΩ, равно отношению числа электронов, отклонившихся на угол θ в телесный угол dΩ, к числу электронов, подошедших в это же время к единице площади. Обозначив поток подошедших электронов через G, можно записать

. (11.8)

Произведение G2πbdb равно потоку электронов через кольцо площадью 2πbdb. Отсюда

. (11.9)

При θ→0 величина σ (υ,θ) стремится к бесконечности, что свидетельствует о большой вероятности рассеяния на малые углы. Для получения интегрального эффективного сечения упругого рассеяния электронов необходимо проинтегрировать дифференциальное сечение по всем углам θ:

. (11.10)

Сечение σ (υ) характеризует полное число рассеянных электронов, отнесенное к единичной плотности потока падающих частиц.

Направленное движение электронов под действием внешнего поля в значительной степени определяется потерями скорости (импульса) при столкновениях с частицами газа. Влияние упругих столкновений на движение электронов учитывается введением интегрального эффективного сечения для передачи импульса (транспортного сечения) σ_m.

Если частица с массой m₁ сталкивается с частицей, масса которой m₂, то при рассеянии на угол θ импульс первой частицы изменится на

v , (11.11)

где v – вектор относительной скорости до столкновения.

При упругом столкновении электрона с медленным атомом компонента импульса электрона в направлении начального движения изменяется на Δp = p(1 – cosθ), поэтому в формуле для транспортного сечения появится множитель (1 – cosθ):

. (11.12)

В уравнения движения электрона в газе входит длина свободного пробега, вычисленная на основе транспортного сечения. Для этого следует воспользоваться формулой (11.7), подставив в нее σ_m (υ). В конкретных задачах нужно учитывать распределение всех сталкивающихся частиц по скоростям и при расчете σ_m производить усреднение.

Для кулоновского взаимодействия заряженных частиц, например для рассеяния потока электронов ионами газа, когда потенциал сил взаимодействия медленно спадает с расстоянием, учет дальних взаимодействий, соответствующих слабым отклонениям электронов (θ→0), дает расходящийся интеграл в формуле (1.12). Для получения приближенного конечного результата приходится вводить ограничения на расстояние, при котором учитывается действие кулоновских сил.

Минимальное расстояние определяется так называемым радиусом ближнего взаимодействия b₀ – расстоянием, при котором взаимная потенциальная энергия сталкивающихся частиц равна по абсолютной величине удвоенной кинетической энергии их относительного движения. Для электрона и положительного иона с зарядом Ze

. (11.13)

За максимальное расстояние принимают дебаевский радиус r_D – радиус области, за пределами которой экранируется поле заряда, внесенного в плазму (см. § 11.4). С учетом этих ограничений, взяв интеграл в формуле (11.12), получим

, (11.14)

где - кулоновский логарифм (величина в пределах от 1 до 20).

Электроны в газовом разряде сталкиваются не только с ионами, но и с другими электронами, а также с нейтральными атомами и молекулами. Для нахождения частоты столкновений электрона с передачей импульса следует сложить частоты столкновений со всеми видами частиц:

, (11.15)

где ν_ml и σ_ml – частота и транспортное сечение столкновений с частицами сорта l; υ_l – относительная скорость. Среднее время между двумя столкновениями τ_m=1/ ν_m. Заметим, что эффективное сечение упругого рассеяния электронов на нейтральных частицах значительно меньше, чем при кулоновском рассеянии, однако этот процесс имеет существенное значение в слабоионизированном газе для установления распределения частиц по энергиям.

При неупругих столкновениях в уравнении закона сохранения энергии появляется член ΔЕ, характеризующий изменение потенциальной энергии частиц за счет перехода в нее части кинетической энергии. Наибольшее значение имеют здесь столкновения электронов с атомами газа, заканчивающиеся возбуждением или ионизацией атомов. Для характеристики этих процессов также используют понятия эффективных сечений, которые могут быть выражены через транспортное сечение σ_m и вероятности w_в, w_i возбуждения и ионизации при столкновении:

(11.16)

Эффективные сечения на единицу объема Q_в = σ_вN₀ и Q_i = σ_iN₀ определяют количество актов возбуждения или ионизации, производимых электроном на единице своего пути. Графики зависимости Q_i и Q_в от энергии электрона представляют собой кривые с максимумом (рис. 11.1, а и б).

Максимальная вероятность возбуждения атома соответствует энергии электрона, лишь несколько большей энергии возбуждения, тогда как максимум вероятности ионизации приходится на энергии электрона порядка нескольких десятков или даже сотен электрон-вольт для различных типов газа. График зависимости эффективного сечения ионизации Q_i от энергии электрона eV (за исключением области максимума) можно описать приближенной эмпирической формулой

, (11.17)

где a и b – константы, зависящие от природы газа.

Рис. 11.1

Эффективные сечения возбуждения и ионизации заметно возрастают при наличии в спектре атомов газов метастабильных энергетических уровней, с которых правилами отбора запрещен самопроизвольный переход электронов на более низкие уровни. Электрон покидает метастабильный уровень лишь в процессе столкновения атома с другой частицей или фотоном. Поэтому среднее время пребывания атома в возбужденном состоянии при наличии метастабильных уровней увеличивается с 10^-8 – 10^-9 с до 10^-4 – 10^-2 с и возрастает вероятность ступенчатого возбуждения или ступенчатой ионизации, когда свободный электрон передает свою энергию возбужденному атому, находящемуся в метастабильном состоянии. При этом, очевидно, для возбуждения или ионизации атома требуется энергия, меньшая энергии при прямом возбуждении или ионизации.

Возможность ступенчатой ионизации определяется также процессом резонансного возбуждения атомов газа. Дело в том, что из возбужденного состояния атом может перейти, испустив квант света, который поглотится другим атомом и в свою очередь приведет его в возбужденное состояние. Последовательная передача возбуждения от атома к атому (до тех пор, пока квант не покинет разрядного промежутка) увеличивает эффективное время пребывания системы в возбужденном состоянии и способствует процессу ступенчатой ионизации.

Зависимость полного эффективного сечения рассеяния электрона Q от его скорости приведена на рис. 11.1, в для инертных газов при р = 1 Па и Т = 273 К. Величина Q может быть пересчитана для других давлений и температур умножением на . Аналогично сечениям возбуждения и ионизации полное сечение имеет максимум при определенных энергиях электрона. В то же время газовая среда почти не рассеивает потока электронов с энергиями порядка 1 эВ. Здесь проявляются волновые свойства электронов, приводящие к их дифракции на атомах газа (эффект Рамзауэра).

Ионизация атомов газа может быть осуществлена также потоком положительных ионов, однако вероятность этого процесса значительно меньше, чем при ионизации атомов потоком электронов. Это связано с большой массой и малой скоростью положительных ионов, в силу чего доля энергии, переданной атому в процессе столкновения, невелика. Энергия, переходящая при неупругом столкновении во внутреннюю энергию частиц с массами m₁ и m₂, сближающихся с относительной скоростью υ, не может превысить

. (11.18)

Масса электрона m_e много меньше массы атома М_а , поэтому, как следует из (11.18), , т.е. при столкновении электрона с атомом на возбуждение атома может быть затрачена почти вся кинетическая энергия электрона. При столкновении же атома с положительным ионом, имеющим массу М_i ≈ М_a, ΔЕ_max не превышает , т.е. ион может передать атому не более половины своей кинетической энергии.

Помимо этого, велика вероятность, что движущийся с малой скоростью положительный ион своим медленно изменяющимся полем лишь сместит энергетические уровни атома, не вызывая межуровневых переходов электронов. После прохождения иона смещение уровней пропадает и энергетическая структура атома восстанавливается, причем его внутренняя энергия в конечном счете не изменяется.

Оценивая возможность передачи энергии иона непосредственно электрону атома при столкновении, следует отметить, что

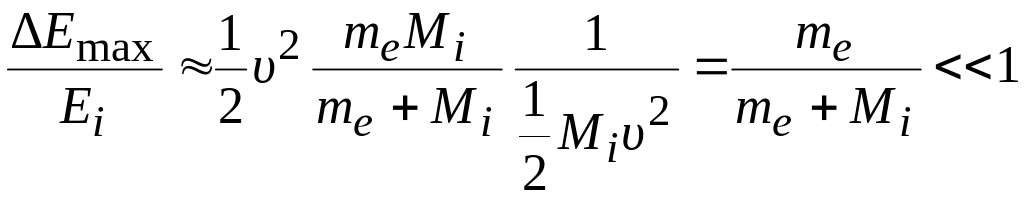, (11.19)

т.е. для передачи электрону энергии порядка eV_i ион должен иметь энергию в несколько килоэлектрон-вольт, а этого в газовом разряде не может быть. Средние энергии ионов в газоразрядной плазме не превышают 10 эВ, а при таких значениях неупругие столкновения ионов с атомами не играют заметной роли.

Так же мала вероятность ионизации атомов при их столкновениях с другими нейтральными атомами. Однако при высоких температурах и давлениях этот процесс имеет существенное значение, так как приводит к термической ионизации газа за счет энергии теплового движения. Легче всего термическая ионизация происходит в газах с низким потенциалом ионизации атомов, особенно в парах щелочных металлов. Высокая степень ионизации достигается здесь уже при температуре 3000 К, тогда как для ионизации инертных газов необходимы температуры свыше 10 000 К (при давлении в несколько сотен паскалей).

Важное значение имеют процессы возбуждения и ионизации атомов газа квантами света. Для прямой фотоионизации энергия кванта должна превышать энергию ионизации eV_i, т.е. излучение должно соответствовать далекой ультрафиолетовой части спектра. Однако возможен и процесс ступенчатой фотоионизации, когда фотоны лишь переводят атом в возбужденное состояние, а дополнительная энергия, необходимая для ионизации, приобретается атомом в результате столкновения с другой частицей. Ступенчатая фотоионизация требует меньших энергий квантов, и ионизирующее излучение может быть в видимой части спектра. Кроме того, ионизирующее излучение может появляться в самом газовом разряде при переходе возбужденных атомов или ионов газа в невозбужденное состояние с испусканием квантов света, достаточных для фотоионизации.

Кинетика заряженных частиц. В результате многочисленных столкновений и обмена энергией устанавливается определенное распределение частиц в газе по координатам и скоростям, характеризуемое функцией распределения. Сведения о движении частиц в газе можно получить из решения кинетического уравнения Больцмана, однако в общем случае это представляет большие трудности.

Из вида кинетического уравнения можно сделать некоторые выводы о свойствах газового разряда. В частности, можно определить условия подобия разрядов. Если рассмотреть два газоразрядных промежутка, геометрически подобных друг другу и заполненных одинаковым газом, то можно показать, что в таких системах функции распределения электронов, а следовательно, и вольт-амперные характеристики одинаковы. Правда, это правило не выполняется в условиях высокой концентрации заряженных частиц, а также в разрядах, где нельзя пренебречь ступенчатой ионизацией, фотоионизацией, термической ионизацией и объемной рекомбинацией носителей заряда.

Из кинетического уравнения можно найти комбинации параметров, инвариантные относительно подобных преобразований, т.е. одинаковые для подобных газоразрядных промежутков. К ним относятся, например, Lp, и др. (здесь L – какой-либо линейный размер разряда или радиус газоразрядной трубки; р – давление; α – коэффициент Таунсенда (см.§11.2). Использование инвариантных параметров позволяет упростить описание процессов в газовом разряде.

Элементарные частицы в объеме газа движутся по сложным траекториям, непрерывно изменяя направление своего движения в результате столкновений. Это сложное движение можно рассматривать как результат суммирования чисто хаотического, беспорядочного движения и направленного движения – под действием электрического поля или за счет градиента концентрации. Соотношение между этими типами движений определяется давлением и напряженностью электрического поля.

Равновесное распределение электронов в газоразрядном промежутке близко к распределению Максвелла – Больцмана. Можно ввести понятия электронной температуры Т_е как меры средней энергии электронов, а также среднеарифметической, среднеквадратичной и невероятнейшей скоростей электронов, вычисляемых по правилам статистики. В процессе упругого столкновения электрон передает атому газа лишь незначительную часть своей энергии, не более 4 m_e / M_a, поэтому средняя энергия электронов при наличии внешнего поля быстро возрастает, и электронная температура может значительно превысить температуру газа и стенок сосуда. Точный вид функции распределения для положительных ионов пока не установлен, однако и здесь условно вводят понятие ионной температуры Т_i.

Во внешнем электрическом поле функция распределения становится несимметричной относительно координатных осей, и у электронов появляется дрейфовая составляющая скорости υ_др, связанная с напряженностью внешнего поля и подвижностью электронов μ_е соотношением , где μ_е также зависит от :

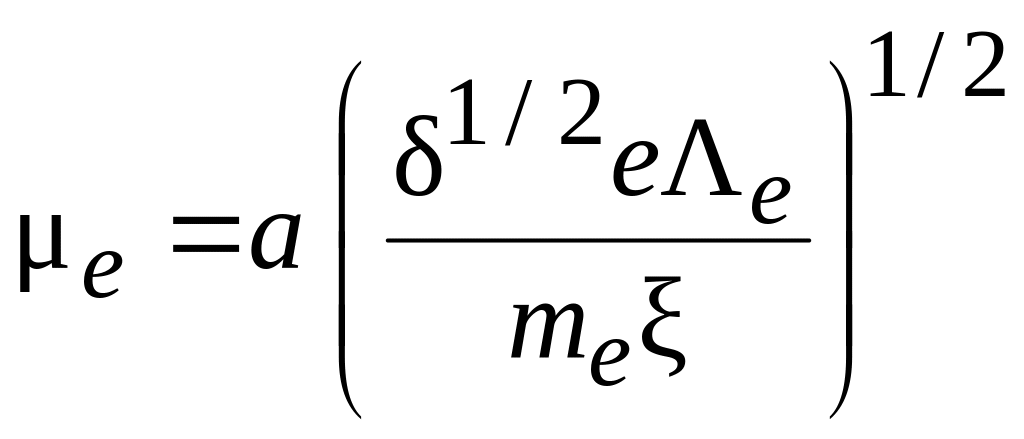. (11.20)

В формуле (11.20) а – константа; δ – коэффициент, равный доле энергии, передаваемой электроном атому при столкновении; Λ_е – средняя длина свободного пробега электрона, определяемая транспортным сечением σ_m (для приближенных расчетов можно брать значения Λ_е, вычисленные на основе полного сечения рассеяния).

Дрейфовая составляющая скорости появляется и у ионов газа, прием их подвижность μ_i связана с подвижностью электронов (в грубом приближении) соотношением

, (11.21)

где Λ_i – средняя длина свободного пробега иона.

Из выражения (11.21) видно, что подвижность ионов газа много меньше подвижности электронов, поскольку M_i » m_e и Λ_e > Λ_i.

Заметное влияние на подвижность положительных ионов оказывают процессы перезарядки. Движущийся ион может при столкновении с атомом или молекулой отобрать от них валентный электрон и превратиться в нейтральный атом. В процессе столкновения скорости частиц практически не изменяются, так что в результате перезарядки появляется быстрый нейтральный атом (бывший ион) и медленный положительный ион (бывший атом или молекула).

Особенно велика вероятность перезарядки, когда ион и атом газа принадлежат одному и тому же элементу. В этом случае перезарядка носит резонансный характер, т.е. внутренняя энергия системы не изменяется и обмен электроном может происходить при большом расстоянии между атомом и ионом. При этом именно перезарядка определяет подвижность иона, которая, так же как и для электронов, обратно пропорциональна корню квадратному из напряженности электрического поля:

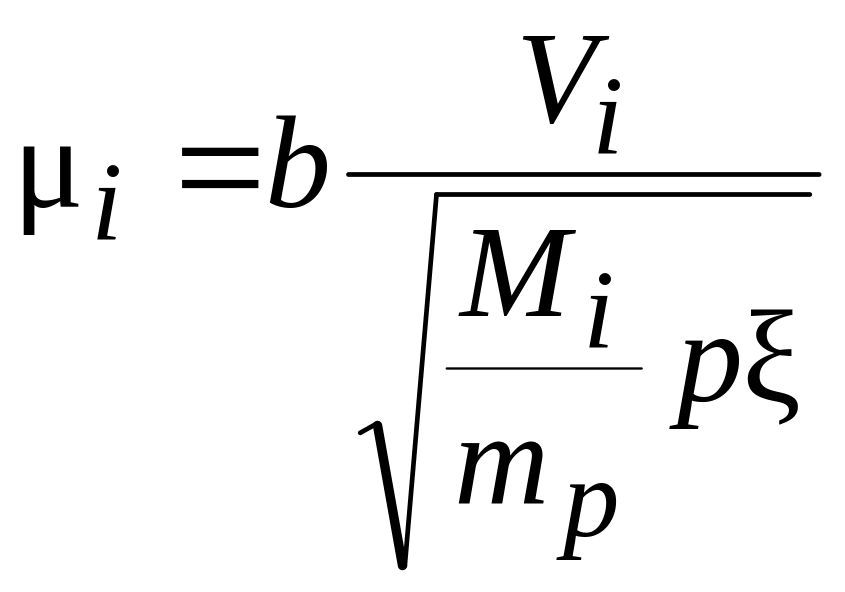. (11.22)

Здесь b – константа; m_p – масса протона.

Рекомбинация зарядов. Одновременно с процессом ионизации газа происходит удаление заряженных частиц из разряда. Оба процесса уравновешиваются, и в стационарном состоянии концентрация заряженных частиц в разряде остается неизменной. Устранение заряженных частиц из разряда может быть связано с одним из следующих процессов:

1) рекомбинацией заряженных частиц противоположного знака в объеме газа;

2) «прилипанием» электронов к нейтральным атомам и молекулам (устранением быстрых частиц);

3) диффузией заряженных частиц к стенкам сосуда с последующей рекомбинацией;

4) рекомбинацией зарядов на электродах.

При рекомбинации положительных ионов с электронами или отрицательными ионами избыточная энергия выделяется в виде рекомбинационного излучения или передается ближайшим элементарным частицам в процессе «тройного столкновения». В случае ступенчатой рекомбинации образуются возбужденные атомы, которые затем переходят с излучением в нормальное состояние. Скорость объемной рекомбинации пропорциональна концентрации зарядов обоих знаков:

, (11.23)

где β – коэффициент рекомбинации.

Коэффициент β определяется скоростью частиц. Чем медленнее движутся частицы, тем больше времени они находятся вблизи друг друга и тем выше вероятность рекомбинации. Коэффициент β может быть определен по скорости уменьшения концентрации заряженных частиц после выключения разряда. Если в момент выключения разряда n₊ = n_- = n₀, то интегрирование выражения (11.23) дает

. (11.24)

Присоединение электронов к атомам газа маловероятно. Значительно выше вероятность присоединения электронов к молекулам газа с последующей рекомбинацией с положительными ионами. Присоединение электронов к нейтральным молекулам газа («прилипание») наиболее вероятно в газах, молекулы которых имеют большое электронное сродство. Столкновение электрона с молекулой или положительным молекулярным ионом может привести к диссоциации, так как энергия электрона, передаваемая молекуле, вызывает нарушение межатомных связей.

В объеме газа электрон находится вблизи иона очень короткий промежуток времени (менее 10^-8 с), поэтому вероятность объемной рекомбинации электрона и иона невелика. Усиленная рекомбинация зарядов происходит на стенках сосуда, к которым диффундируют электроны и ионы из объема газа и около которых движение зарядов пространственно ограничено. Вероятность рекомбинации у стенок велика ещё и потому, что стенка способна поглотить энергию, выделяемую при рекомбинации. Процесс рекомбинации на металлических электродах заключается в переходе свободных электронов из разрядного промежутка в металл под действием поля у границы кристаллической решетки, а также в туннельном переходе электронов металла сквозь потенциальный барьер у его границы на один из свободных уровней приближающегося положительного иона с образованием нейтрального атома газа в возбужденном или нормальном состоянии.

Преобладание того или иного вида рекомбинации в газовом разряде определяется прежде всего давлением газа. При р < 10² Па преобладает поверхностная ионизация, при р > 10³ Па – объемная ионизация.