3.2.3. Расчет второй сетки лучевого тетрода

Исходя из особенностей построения лучевых конструкций:

,  для стержневой сетки;

,  для спиральной сетки.

Для расчета коэффициента заполнения второй сетки задается диаметр сеточных проводников исходя из соотношения .

В рассчитанной системе электродов лучевого тетрода можно оценить фокусировку электронного потока, исходя из оптимальности нахождения кроссовера F_m в плоскости второй сетки (рис. 3.5) [2].

При условии

,

г

Рис. 3.5

де ; U_∂1 ≈D₁ ∙E_c2; . Так как при учете объемного заряда фокусное расстояние увеличивается, фокусировку можно считать удовлетворительной при выполнении соотношения . В случае существенного расхождения полученной СЭ с этим условием следует пересчитать систему электродов, используя другие значения или . При этом надо иметь в виду, что увеличение приводит к росту ( ), а увеличение  к росту и .

Задав проницаемость второй сетки в пределах 0,01…0,04, определим расстояние «сетка втораяанод» ( ):

. (3.17)

Найденное значение ( ) проверяется с двух сторон (слева  на отсутствие динатронного эффекта, справа  на отсутствие фиктивного катода):

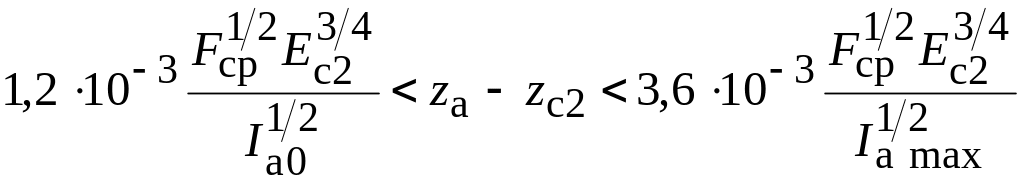. (3.18)

Здесь  средняя площадь сечения электронного потока между второй сеткой и анодом; . Постоянная составляющая тока анода . Напряжение на второй сетке определяется режимом работы лампы. В случае невыполнения проверок (3.18) слева или справа значение ( ) пересчитывается при задании, соответственно, меньших или больших значений и . Если при этом левое неравенство по-прежнему не выполняется, то для предотвращения динатронного эффекта применяется камерный анод [2].

После проверки найденной величины ( ) определяется расстояние «катоданод» и диаметр анода лучевого тетрода .

В случае применения камерного анода в лучевой конструкции в зависимости от формы лучей камеры могут быть как вертикальными при стержневой сетке, так и горизонтальными при спиральной сетке. Очевидно, что в конструкции лучевого тетрода ребра камер должны быть в тени сеточных проводников [2].

В результате расчета по приведенной методике определяются геометрические размеры электродов СЭ триодной и тетродной конструкций (при этом может быть использована программа MathCad). Таким образом производится приближенный (первичный) синтез системы электродов электронной лампы, которая может быть использована в качестве эскизного варианта разрабатываемого прибора. В дальнейшем этот вариант может анализироваться программами более высокого уровня, как аналитическими, так и численными, и доводиться до получения необходимых значений выходных параметров.

4. Расчет систем формирования слаботочных электронных потоков

Маломощные электронные пушки (прожекторы) применяются для формирования узких электронных пучков диаметром мм. Оптическая схема прожектора содержит два элемента: триодный прожектор (иммерсионный объектив), предназначенный для начального формирования пучка, и проекционную линзу, обеспечивающую фокусировку пучка на мишень или экран электронно-лучевого прибора.

К основным параметрам прожектора относятся потенциал запирания, плотность тока с катода, радиус эмитирующей торцевой поверхности катода, угол раствора пучка на выходе прожектора, размер кроссовера и некоторые другие. Данные параметры определяются главным образом геометрией и потенциалами электродов иммерсионного объектива.

Геометрия триодного прожектора показана на рис. 4.1.

D_м

D_м.а

D_к.м

R_м

r_кр

r_к

r_раб

Рис. 4.1

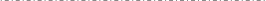
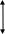
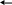
Наиболее существенное влияние на поле у катода, а следовательно, на ток пучка отказывает потенциал модулятора. Влияние его аналогично действию управляющей сетки обычного триода. При уменьшении потенциала модулятора ток пучка уменьшается до нуля и прожектор запирается. Потенциалом запирания прожектора называют такой отрицательный по отношению к катоду потенциал модулятора, при котором ток пучка примерно равен нулю, точнее, составляет 0,5 % от рабочего тока пучка. Существует ряд эмпирических формул для расчета потенциала запирания; большинство из них даны, например, в [1].

Для выбора первоначальной геометрии электродов прожектора наиболее часто пользуются следующим выражением:

, (4.1)

где  потенциал запирания прожектора;  потенциал анода; при ; ; .

Модуляционная характеристика, т. е. зависимость тока катода (пучка) от потенциала модулятора, описывается выражением

, (4.2)

где  ток катода;  постоянная, зависящая от геометрии прожектора;  управляющий фактор;  рабочий потенциал модулятора.

Показатель степени α модуляционной характеристики отличается от показателя 3/2 в законе «степени трех вторых» для электронных ламп. В зависимости от геометрии прожектора его величина может быть 2,5…3,5, и объясняется это тем, что при изменении потенциала модулятора вместе с изменением плотности тока изменяется радиус эмитирующей поверхности катода . Радиус эмитирующей поверхности катода определяется выражением

, (4.3)

где показатель степени .

Как правило, если неизвестны особенности геометрии иммерсионного объектива, в предварительных расчетах выбирают

; ; .

Следующим параметром прожектора является плотность тока, снимаемая с центра катода. Центр эмитирующей поверхности катода прожектора является наиболее нагруженным, и уменьшение во времени плотности тока катода определяет срок службы большинства электронно-лучевых приборов. Поэтому катод должен обеспечивать с запасом допустимую плотность тока , которая определяется геометрией прожектора:

. (4.4)

Как правило, в прожекторе используются термокатоды. При выборе типа и режима работы катода запас по эмиссии задается условием , где максимальная плотность тока эмиссии находится по закону Ричардсона  Дэшмана (см. 3.1).

Угол расхождения пучка определяет аберрации фокусирующей и отклоняющей линз: чем меньше , тем меньше аберрации. Оценить величину угла расхождения прожектора можно по формуле

. (4.5)

Из (4.5) видно, что угол расхождения пучка зависит от радиуса эмитирующей поверхности катода , а также расстояния «катодмодулятор» и толщины модулятора . Отсюда следует, что целесообразно выбирать и , по возможности, минимальными. Минимальные размеры и ограничены технологическими возможностями и тепловым расширением электродов: расстояние «катодмодулятор» должно быть не менее 70 мкм, толщина модулятора  не менее 40 мкм. Следует отметить, что для высоковольтных прожекторов угол расхождения пучка на выходе прожектора является основной причиной аберраций. Поэтому геометрию прожектора можно выбирать в этом случае, например, из соображений наиболее простой технологии изготовления и сборки прожектора.

Распределение плотности тока по поверхности катода определяется выражением

(4.6)

Наконец, последним из рассматриваемых параметров являются распределение плотности тока в кроссовере и размер кроссовера. Обычно кроссовер является объектом для изображения фокусирующей (проекционной) линзы, и его размер обусловливает размер электронного пучка на мишени или экране электронно-лучевого прибора. Размер кроссовера определяется, по крайней мере, тремя факторами  тепловыми скоростями электронов на катоде, влиянием аберраций иммерсионной линзы и расталкивающим действием собственного объемного заряда пучка. Последние два фактора могут быть учтены лишь точными методами анализа с применением ЭВМ. Влияние тепловых скоростей на распределение плотности тока в кроссовере оценивается выражением

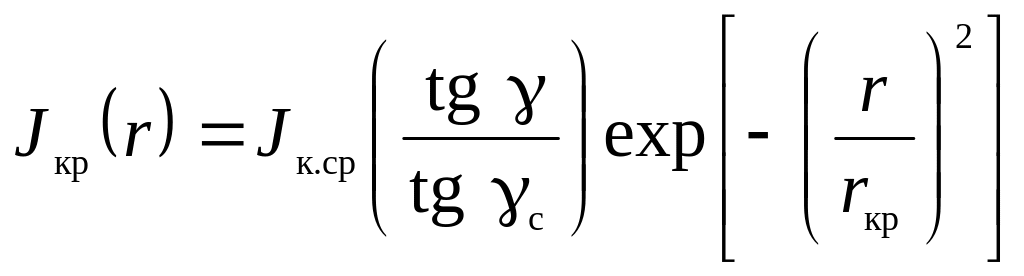, (4.7)

где ;  средняя плотность тока катода;  радиус кроссовера. Выражения (4.1)(4.7) позволяют выбрать первоначальный вариант геометрии прожектора по заданному потенциалу анода , потенциалу запирания , плотности тока катода и току пучка . Для определения геометрии рассчитывают два семейства кривых  зависимости потенциала запирания (рис. 4.2, где 1  ; 2  0,4; 3  0,8) и плотности тока в центре катода (рис. 4.3, где 1  мм; 2  0,2 мм; 3  0,3 мм) от параметра, определяющего геометрические размеры прожектора . Расчеты выполняются, соответственно, по формулам (4.1) и (4.4). Управляющий фактор определяют из выражения (4.2). Результаты, представленные на рис. 4.2 и 4.3, соответствуют следующим исходным данным: В, В, мкА, А/см². По заданному потенциалу запирания находят диапазон изменения безразмерной величины . В данном случае (рис. 4.2).

Исходя из срока службы катода и его экономичной эксплуатации, область значений плотности тока в центре катода ограничивают, как было изложено, диапазоном . Зная диапазон изменения и , по рис. 4.3 определяем область рабочих значений (заштрихованный прямоугольник). Этот прямоугольник пересекает несколько кривых заданного семейства. Можно выбрать любую из них с некоторым значением радиуса модулятора, но целесообразно использовать малые значения . При этом расстояние «катодмодулятор» и толщина модулятора будут также малыми и электронный пучок будет более параксиальным. Следует отметить, что сумма не должна быть меньше 0,12 мм из-за сложностей изготовления и сборки прожектора при его параметрах, воспроизводимых для партии приборов. Например, выбрав на рис. 4.2 кривую 3, соответствующую , определим, что . На рис. 4.3 для полученного значения в заштрихованной области выбираем кривую 1, соответствующую . Отсюда плотность тока в центре катода ; расстояние «модуляторанод» ; «катодмодулятор» с учетом толщины модулятора  . Выбрав, например, , получим . Указанные значения хорошо реализуются при изготовлении и сборке прожекторов по существующей технологии.

J(0), A/см²

U_м0, B

0 0,4 0,8 1,2 χ 0 0,4 0,8 1,2 χ

80

60

40

20

0,4

0,8

1,2

1,6

U_а – const

t – const

2

3

1

2

3

1

Рис. 4.2 Рис. 4.3

Для расчета ЭОС прожектора на ЭВМ может быть использована программа MATLAB. Вычисления проводятся по выражениям (4.1)(4.7). В процессе работы задаются геометрические размеры ЭОС прожектора, ЭВМ рассчитывает параметры ЭОС, соответствующие введенной геометрии. Если полученные параметры не удовлетворяют исходным данным, то необходимо изменить геометрию и продолжить расчет. В результате последовательного анализа определяется геометрия ЭОС, удовлетворяющая с заданной точностью исходным условиям. Далее рассчитываются модуляционная характеристика и распределения плотности тока пучка на катоде и в кроссовере. Если полученные в результате расчета геометрия и характеристики удовлетворяют требованиям, предъявляемым к прожекторам заданного в исходных данных класса электронно-лучевых приборов, то при необходимости можно перейти к более точным методам анализа параметров и характеристик прожектора.