1.3. Системы формирования потоков заряженных частиц в плазменных приборах и устройствах

Рассмотренные системы формирования интенсивных электронных пучков для технологических целей позволяют получить электронные пучки с высокими параметрами, однако имеют существенные недостатки, обусловленные невысокой надежностью и долговечностью термокатодов, особенно при повышенных давлениях, характерных для технологических ЭЛУ. Кроме того в ряде случаев в технологии необходимо использовать потоки ионов. Это обусловило создание плазменных источников заряженных частиц. Одним из таких источников является дуоплазмотрон, система формирования которого приведена на рис. 1.9 [3].

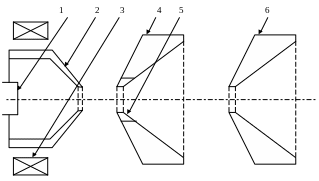
Рис. 1.9

Несамостоятельный дуговой разряд горит между накаленным катодом 1 и анодом 4. Форма электрода 2 обеспечивает сжатие плазмы в выходном окне (осуществляется геометрическое контрагирование). Дополнительное сжатие плазмы достигается магнитной фокусирующей системой 3. В выходном окне анода предусмотрена жаропрочная вставка 5. Электрод 6 в зависимости от знаков поданного на него напряжения вытягивает из плазмы поток электронов или ионов.

Для работы при низком вакууме, особенно с использованием активных газовых сред, применяются пушки с ненакаливаемыми катодами, в частности газоразрядные электронные пушки (ГРЭП) на основе высоковольтного тлеющего разряда с прианодной плазмой. Работа ГРЭП с холодным катодом основана на использовании тлеющего разряда лучевой формы, возникающего при давлениях единицысотни паскалей, когда в разряде преобладает направленное движение заряженных частиц над хаотическим. На рис. 1.10 представлены схемы формирования электронных пучков в газоразрядных электронных пушках с прианодной плазмой. В пушках с большой анодной апертурой конфигурация плазменной границы подобна форме катода. Простота холодных катодов и наличие прозрачного плазменного анода позволяют относительно просто формировать профильные электронные пушки различной конфигурации (на рис. 1.10: а  сходящийся пучок; б  трубчатый; в  ленточный) [1].

Рис. 1.10

Током пучка в ГРЭП при неизменном ускоряющем напряжении можно управлять, регулируя параметры плазмы. Для этой цели применяют системы управления давлением в разрядной камере пушки или управляющие электроды, позволяющие возбуждать вспомогательный разряд и изменять таким образом концентрацию плазмы, а следовательно, и ток пучка. Пучки, формируемые ГРЭП, проводят в зону обработки, используя те же принципы электронной оптики, что и для термокатодных пушек.

2. Обобщенные методы расчета систем формирования потоков заряженных частиц вакуумных и плазменных приборов и устройств

Несмотря на большое разнообразие ВППУ, для этих приборов и устройств применимы обобщенные методы численного моделирования СФ. Правда, в обобщенном виде возможен лишь анализ СФ, т. е. задав геометрию электродов, потенциалы, внешние магнитные поля, давление и род газа в канале, можно рассчитать электрические и магнитные поля в системе, движение заряженных частиц в поле с учетом влияния газовой среды и, получив параметры и характеристики потока, сделать вывод о пригодности данной системы для решения поставленной задачи. Если параметры потока не удовлетворяют задаче, то с помощью методов оптимизации меняют геометрию или параметры СФ и повторяют расчет до получения желаемого результата.

В общем случае для нахождения электростатического поля в СФ необходимо решить уравнение Пуассона

, (2.1)

где  плотность объемного заряда (электронная или ионная) в области СФ;  диэлектрическая постоянная. Как правило, решение уравнения (2.1) ищут в виде , где  потенциал, создаваемый электродами СФ;  потенциал, обусловленный пространственным зарядом. Аналогичным образом определяется магнитное поле:

, (2.2)

где  магнитное поле, создаваемое внешней магнитной системой;  магнитное поле, обусловленное движением зарядов в СФ.

Для описания бесстолкновительного распространения заряженных частиц чаще всего используют уравнение движения, записанное в форме Ньютона:

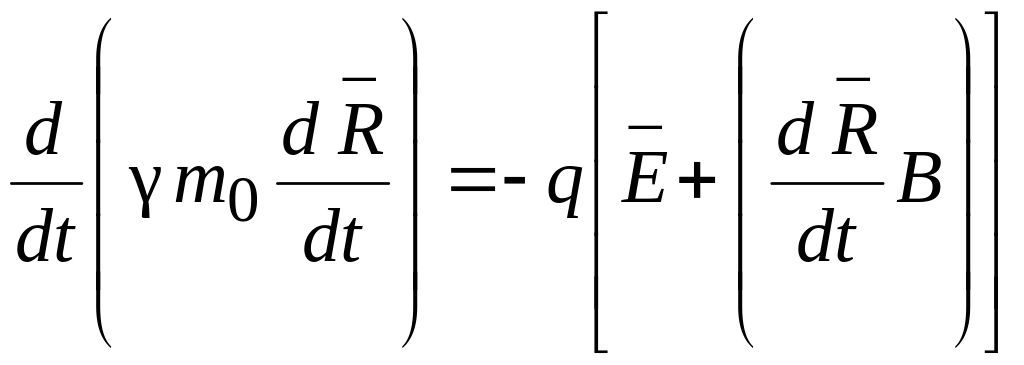, (2.3)

где  релятивистский фактор;  вектор напряженности суммарного электрического поля;  вектор индукции суммарного магнитного поля.

Движение заряженных частиц в газовой среде сопровождается следующими основными процессами: упругим рассеянием; возбуждением атомных электронов; ионизацией атомов и молекул газа; образованием лавин (электронных и ионных); зарядовым обменом; рекомбинацией электронов и ионов. Вероятность того или иного процесса определяется родом и давлением газа, энергией и типом заряженных частиц. Количественно эта вероятность описывается с помощью сечения взаимодействия . Пробег частиц между соударениями находят из распределения

, (2.4)

где  связан с полным сечением взаимодействия соотношением ;  концентрация молекул газа.

В результате указанных взаимодействий меняются направленное движение заряженных частиц и их энергия, образуются новые заряженные частицы. Отбор электронов от катода при равномерной структуре электростатического поля в прикатодном пространстве подчиняется закону «степени трех вторых»

, (2.5)

где  потенциал на расстоянии от поверхности катода.

Решая согласованную систему уравнений (2.1)(2.5), можно провести анализ любой СФ. Аналитического решения системы (2.1)(2.5) не существует, возможно лишь численное решение, точность и быстрота которого определяются параметрами ЭВМ, выбранными численными методами и особенностями конкретной СФ.

Расчет электронного прибора численными методами на ЭВМ требует учета его конкретных особенностей.

Так, в электронных лампах основную трудность составляет расчет траекторий электронов вблизи сеточных проводников, имеющих весьма разнообразную конфигурацию, что приводит к сложной форме электростатического поля вблизи них. В общем случае это требует решения трехмерной задачи, особенно при использовании так называемых объемных сеток, когда на несущий сеточный стержень навивается дополнительная спираль.

В передающих электронно-лучевых трубках наиболее сложной задачей является расчет электростатического поля вблизи фотокатода. Это обусловлено тем, что у фотокатода электроны имеют малые энергии (менее 1 эВ), а затем ускоряются до энергий порядка десятка килоэлектрон-вольт. Начальные энергии фотоэлектронов существенно влияют на качество электронного изображения, формируемого на мишени, поэтому погрешность расчета потенциала в прикатодной области должна быть в 5…10 раз меньше, чем потенциал, соответствующий начальной энергии фотоэлектрона.

В осциллографических трубках основные сложности связаны с проектированием отклоняющей системы, обеспечивающей максимальную чувствительность и минимальные аберрации. Как правило, такие системы не имеют аксиальной симметрии. Следовательно, их расчет требует решения трехмерной задачи.

Особенности системы формирования и отклонения электронных пучков в цветных кинескопах связаны с наличием трех электронных пучков, совмещенной электромагнитной системы отклонения и коррекции, а также сложного электронного узла.

Проектирование приборов с остаточной газовой средой также требует учета характерных особенностей этих приборов.

Как показывает практика, параметры современных ЭВМ не позволяют однозначно выбрать математическую модель и тем более численные методы ее реализации на ЭВМ.

Обычно первым этапом расчета СФ является нахождение распределения потенциала и напряженности магнитного поля в выбранной системе формирования электронного пучка. Предложено большое количество численных методов решения данной задачи, но в настоящее время наиболее широкое распространение получили методы конечных разностей, интегральных уравнений и конечных элементов. Достоинства и недостатки этих методов исследованы, но однозначного ответа на вопрос, в каком случае какой метод использовать, не существует, и требуются дальнейшие исследования в данной области.

Расчет процесса формирования электронного пучка еще более сложен, и решение этой задачи с учетом всего многообразия физических факторов в настоящее время невозможно. Наиболее простым методом является траекторный анализ: по результатам полученного распределения потенциала и напряженности магнитного поля рассчитывается каким-либо численным методом ряд траекторий, по виду которых судят о параметрах пучка. Однако для ряда приборов и устройств существенны процессы у катода, моделирование которых требует расчета огромного количества электронных траекторий с разными начальными условиями, что осуществить на современных ЭВМ крайне затруднительно.

Развитием метода траекторного анализа явилось использование интегральных преобразований для расчета параметров пучка на базе расчета конкретного числа характерных траекторий, что приводит к ряду трудно оцениваемых погрешностей. Широко распространенным является также аберрационный метод, основанный на расчете коэффициентов аберраций по рассчитанному с высокой точностью распределению потенциала. Данный метод является эффективным для оценки характеристик СФ, но не в целом процесса формирования пучка. Перспективен также фазовый метод, основанный на определении зависимости между текущими и начальными координатами и скоростями, который позволяет определить параметры и структуру потока заряженных частиц.

С учетом вышеизложенного единой математической модели, отражающей все многообразие СФ вакуумных и плазменных приборов и устройств, не существует и при автоматизированном проектировании целесообразно создание и исследование нескольких математических моделей, отражающих физические процессы, характерные только для определенного класса устройств. При этом, как правило, при моделировании СФ применяют две модели. Первая использует достаточно простые эмпирические формулы, связывающие характеристики пучка с геометрией и потенциалами СФ. Погрешность этих формул велика (15…20 %), однако их можно использовать для быстрого предварительного поиска геометрии и электрического режима (первичного синтеза [6]). Результаты расчетов служат хорошим начальным приближением для последующих вычислений по второй, более точной модели, которая предусматривает решение самосогласованной системы уравнений (2.1)(2.5) с учетом характерных особенностей СЭ и ЭОС. Далее рассмотрены несколько вариантов эмпирических моделей для различных систем формирования.