1.1.1.6.5Достоинства и недостатки

Достоинства:

• Один из самых быстродействующих (на практике) из алгоритмов внутренней сортировки общего назначения.

• Прост в реализации.

• Требует лишь   дополнительной памяти для своей работы. (Не улучшенный рекурсивный алгоритм в худшем случае   памяти)

• Хорошо сочетается с механизмами кэширования и виртуальной памяти.

• Существует эффективная модификация (алгоритм Седжвика) для сортировки строк — сначала сравнение с опорным элементом только по нулевому символу строки, далее применение аналогичной сортировки для «большего» и «меньшего» массивов тоже по нулевому символу, и для «равного» массива по уже первому символу.

Недостатки:

• Сильно деградирует по скорости (до 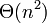 ) при неудачных выборах опорных элементов, что может случиться при неудачных входных данных. Этого можно избежать, используя такие модификации алгоритма, как Introsort, или вероятностно, выбирая опорный элемент случайно, а не фиксированным образом.

• Наивная реализация алгоритма может привести к ошибке переполнения стека, так как ей может потребоваться сделать   вложенных рекурсивных вызовов. В улучшенных реализациях, в которых рекурсивный вызов происходит только для сортировки меньшей из двух частей массива, глубина рекурсии гарантированно не превысит  .

• Неустойчив — если требуется устойчивость, приходится расширять ключ.

1.1.1.7Пирамидальная сортировка

Ал­го­ритм пи­ра­ми­даль­ной сор­ти­ров­ки по-ан­глий­ски на­зы­ва­ет­ся «Heap Sort». «Heap» пе­ре­во­дит­ся, как «ку­ча». В свя­зи с этим пи­ра­ми­даль­ную сор­ти­ров­ку ещё на­зы­ва­ют «сор­ти­ров­ка ку­чей»

Пи­ра­ми­даль­ная сор­ти­ров­ка бы­ла пред­ло­же­на Дж. Уи­льям­сом в 1964 го­ду. Это ал­го­ритм сор­ти­ров­ки мас­си­ва про­из­воль­ных эле­мен­тов; тре­буе­мый им до­пол­ни­тель­ный объ­ём па­мя­ти не за­ви­сит от ко­ли­че­ства ис­ход­ных дан­ных. Вре­мя ра­боты ал­го­рит­ма  -  в сред­нем, а так­же в луч­шем и худ­шем слу­ча­ях.

1.1.1.7.1Понятие пирамиды

Двои́чная ку́ча, пирами́да, или сортиру́ющее де́рево — такое двоичное дерево, для которого выполнены три условия:

1. Значение в любой вершине не меньше, чем значения её потомков.

2. Каждый лист имеет глубину (расстояние до корня) либо d либо d-1. Иными словами, если назвать слоем совокупность вершин, находящихся на определённой глубине, то все слои, кроме, быть может, последнего, заполнены полностью.

3. Последний слой заполняется слева направо.

Удобная структура данных для хранения сортирующего дерева  - массив A, у которого первый элемент, A[1] — элемент в корне, а потомками элемента A[i] являются A[2i] и A[2i+1] (при нумерации элементов с первого). При нумерации элементов с нулевого, корневой элемент — A[0], а потомки элемента A[i] — A[2i+1] и A[2i+2]. При таком способе хранения условия 2 и 3 выполнены автоматически. Ро­ди­тель уз­ла име­ет но­мер  :

Рис. 4.1. Пример нумерации элементов сортирующего дерева

Высота кучи определяется как высота двоичного дерева. То есть она равна количеству рёбер в самом длинном простом пути, соединяющем корень кучи с одним из её листьев. Высота кучи есть  , где N — количество узлов дерева.

Важ­ной опе­ра­ци­ей для пирамиды яв­ля­ет­ся от­де­ле­ние по­след­не­го (в смыс­ле ну­ме­ра­ции) эле­мен­та от пи­ра­ми­ды. Не­труд­но до­ка­зать, что в этом слу­чае дво­ичное де­ре­во оста­ёт­ся по­чти за­пол­нен­ным, и все свой­ства пи­ра­ми­ды со­хра­ня­ются.