Методические указания / Нелинейные структуры данных

1890

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования «Липецкий государственный технический университет»

Кафедра автоматизированных систем управления

НЕЛИНЕЙНЫЕ СТРУКТУРЫ ДАННЫХ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для студентов

к лабораторным работам по курсу «Структуры и алгоритмы компьютерной обработки данных»

Составитель: М. Г. Журавлева

Липецк 2009

УДК 681.3.01 (07)

Ж 911

Журавлева, М. Г. Нелинейные структуры данных: методические указания к лабораторным работам по курсу «Структуры и алгоритмы компьютерной обработки данных» / М. Г. Журавлева. – Липецк: ЛГТУ, 2009. – 24 с.

Предназначены для студентов направлений подготовки бакалавров 230100.62, 200500.62 и инженеров 230101.65; 230102.65; 230104.65; 230105.65; 220501.65; 230401.65; 010503.65.

Рассмотрены принципы построения и алгоритмы обработки двоичных и сильноветвящихся деревьев, алгоритмы обхода графов и построения минимальных остовных деревьев на графах.

Табл. 3. Рис. 10. Библиогр.: 5 назв.

Рецензент В. А. Алексеев.

Липецкий государственный технический университет, 2009

2

1. Теоретические положения

1.1. Деревья. Основные понятия

Дерево – совокупность элементов, называемых узлами (один из которых определен как корень), и отношений, образующих иерархическую структуру узлов. Узлы могут быть элементами любого типа. Формально дерево можно рекуррентно определить следующим образом.

1.Один узел является деревом. Этот же узел является корнем этого дерева.

2.Пусть n – узел, а T1, T2, ..., Tk – деревья с корнями n1, n2, ..., nk соответственно. Можно построить новое дерево, сделав n родителем узлов n1, n2, ..., nk. В этом дереве n будет корнем, а T1, T2, ..., Tk – поддеревьями этого корня. Узлы n1, n2, ..., nk называются дочерними узлами узла n. Узлы, находящиеся на одном уровне (в частности, узлы n1, n2, ..., nk), называют соседними (в некоторых источниках – братьями или сест-

рами).

Пустую структуру или дерево без узлов называют также нулевым (пустым) деревом. Путем из узла n1 в узел nk называется последовательность узлов n1, n2, ..., nk, где для всех i, i = 1, 2, ..., k, узел ni является родителем узла ni+1. Длиной пути называется число, на единицу меньшее числа узлов, составляющих этот путь. Путем нулевой длины будет путь из любого узла к самому себе. Если существует путь из узла а в узел b, то в этом случае узел a называется предком узла b, а узел b – потомком узла a. Число непосредственных потомков (дочерних узлов) внутренней вершины называют ее степенью. Степень дерева определяется максимальной из степеней всех узлов. Предок или потомок узла, не являющийся таковым самого себя, называется истинным предком или истинным потомком соответственно. Только корень дерева не имеет истинного предка. Если узел не имеет истинных потомков, он называется терминальной

3

вершиной или листом, в противном случае – нетерминальной вершиной или внутренним узлом. Поддерево какого-либо дерева можно определить как узел – корень поддерева – вместе со всеми его потомками. Высотой узла называется длина самого длинного пути из этого узла до какого-либо листа. Высота дерева совпадает с высотой корня. Глубина узла x определяется как длина пути от корня до узла x. Ее часто называют просто длиной пути к x. В таком случае корень имеет длину пути 0, его дочерние узлы – длину пути 1 и т.д. Длина пути всего дерева определяется как сумма длин путей всех его узлов. Она называется длиной внутреннего пути. Часто каждому узлу дерева сопоставляется метка, ключ или иначе – значение, которое хранится в узле [1]. Дочерние узлы могут упорядочиваться справа налево. Если порядок дочерних узлов игнорируется, дерево называется неупорядоченным, в противном случае – упорядоченным. Особое значение имеют упорядоченные деревья второй степени. Они называются двоичными или бинарными. Двоичное дерево определяется как конечное множество узлов, пустое, либо состоящее из корня с двумя отдельными двоичными деревьями, которые называются левым и правым поддеревьями этого корня. Деревья степени больше двух называются сильноветвящимися деревьями.

Существует несколько способов прохождения (обхода) всех узлов дерева. Три чаще всего используемых способа обхода дерева называются обход в прямом порядке (сверху вниз), обход в обратном порядке (снизу вверх) и обход во внутреннем порядке (симметричный, слева направо). Рекурсивно их можно определить следующим образом.

•Если дерево Т является нулевым деревом, то в список обхода заносится пустая запись.

•Если дерево Т состоит из одного узла, то в список обхода записывается этот узел.

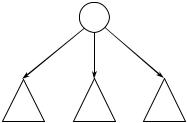
• Далее, пусть Т – дерево с корнем n и поддеревьями Т1, Т2, ..., Тk (см. рис. 1). Для различных способов обхода выполняется следующее:

4

непосредственно перед ее выполнением функция Search(m) возвратила нулевой узел.

6.Delete(m). Удаляет узел с ключом m.

7.Parent(n). Возвращает родителя узла n. Если n является корнем, возвращается нулевой узел.

8.LeftMostChild(n). Возвращает самый левый дочерний узел узла n. Если n является листом, возвращается нулевой узел.

9.RightSibling(n). Возвращает правого соседа узла n и нулевой узел, если такового не существует. Для этого находится родитель p узла n и все дочерние узлы p, затем среди этих потомков находится узел, расположенный непосредственно справа от узла n.

10.MakeNull(). Делает дерево пустым.

Основными операциями являются поиск, включение и удаление. В неупорядоченных несбалансированных деревьях поиск или поиск с включением можно осуществлять, задавшись одним из правил обхода. Без специальных оговорок, удалять в таких деревьях можно только терминальные вершины и вершины, имеющие одного непосредственного потомка (при этом удаляемый узел заменяется своим дочерним узлом). В работе следует использовать одну из следующих стратегий для удаления внутренних узлов: удаляемый узел, имеющий более одного потомка, заменяется либо самым левым, либо самым правым дочерним узлом.

1.2. Реализация деревьев

Представление деревьев с помощью массивов

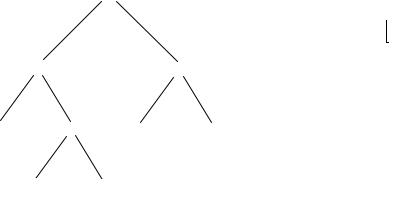
Пусть T – дерево с n узлами: 0, 1, ...n-1. Наиболее простым представлением дерева Т является линейный массив А, где каждый элемент А[i] соответствует родителю узла i. Положим, что корню дерева соответствует значение -1. Тогда А[i] = j, если узел j – родитель узла i, и A[i] = -1, если i является корнем

(см. рис. 2).

6

Представление деревьев с использованием списков дочерних узлов

Важным способом реализации дерева является формирование списка дочерних узлов для каждого его узла. Списки можно представлять любым из соответствующих методов, но так как у узлов часто бывает переменное число дочерних узлов, часто используются связные списки.

8

9

заголовки

Рис. 3. Представление дерева в виде списков дочерних узлов На рис. 3 в виде совокупности связных списков представлено дерево, по-

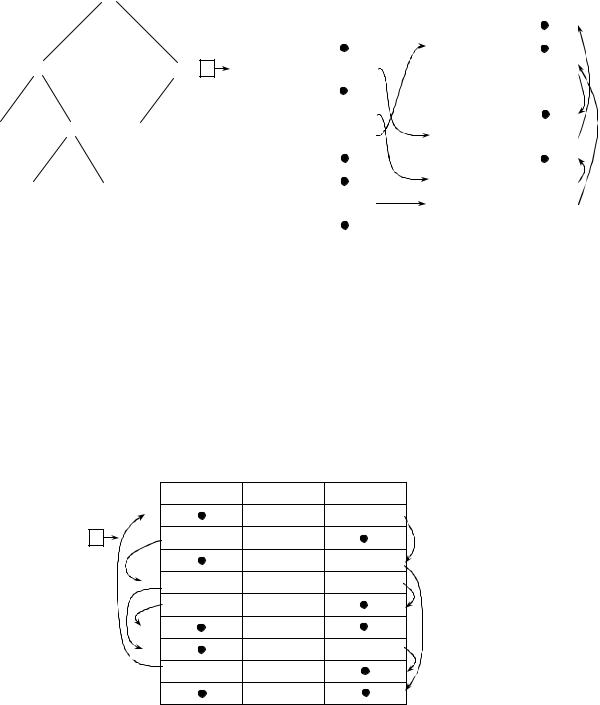
казанное на рис. 2. Здесь используется массив указателей-заголовков, индексированных номерами узлов. Любой заголовок узла i указывает на связный список элементов, являющихся дочерними узлами данного узла, расположенных в порядке слева направо. Аналогичное дерево можно построить без использования указателей, с помощью двух массивов структур. В одном из них хранятся ключи с соответствующими заголовками, имеющими произвольное местоположение. В другом – цепочки дочерних узлов для каждого заголовка ( рис. 4). Например, узел E дерева, изображенного на рис. 4, имеет три дочерних узла (G, H, I) с индексами в первой таблице 1, 3, 9 соответственно. Заголовок, соответствующий ключу E, из первой таблицы содержит индекс 8 второй таблицы. В первом поле структуры с этим номером хранится индекс 1 ключа G, второе поле содержит индекс (в той же таблице), соответствующий структуре, содержащей индекс следующего ключа (дочернего узла) из первой таблицы и т.д.

8

указатели на аналогичные структуры, количество которых равно степени дерева:

struct Tree {

Tree *leftmost_child;

Tree *right_sibling_1;

Tree *right_sibling_2;

...

Tree *right_sibling_k; //для дерева степени k+1 };

1.3. АВЛ-деревья

Оптимальным для хранения в памяти является дерево, у которого на каждом уровне размещается максимально возможное число узлов. Такое дерево называется сбалансированным. Двоичное дерево называется идеально сбалансированным, если число вершин в его левых и правых поддеревьях отличается не более чем на единицу. Поддержание идеальной сбалансированности требует слишком больших накладных расходов. Советскими математиками Адельсо- ном-Вельским и Ландисом предложено менее строгое определение сбалансированности деревьев: двоичное дерево называется сбалансированным в том и только в том случае, когда высоты двух поддеревьев каждой из вершин дерева отличаются не более, чем на единицу. Такие деревья стали называть АВЛдеревьями [2, 3].

Рассмотрим аспекты балансировки АВЛ-дерева при выполнении операций включения и исключения ключей. Пусть рассматриваемое дерево состоит из корневой вершины r и левого (L) и правого (R) поддеревьев. Обозначим через hl высоту L, а через hr - высоту R. Пусть выполняется операция включения, и новый ключ включается в поддерево L. Если высота L не изменяется, то не изменяются и соотношения между высотами L и R, и свойства АВЛ-дерева со-

10