Лабораторные работы / ЛР 31 Изучение магнитного поля Земли

ЛАБОРАТОРНАЯ РАБОТА № 31

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ

ЦЕЛЬ РАБОТЫ: измерение горизонтальной составляющей вектора индукции магнитного поля Земли; изучение устройства и принципа действия тангенс-гальванометра.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: тангенс-гальванометр, переклю-

чатель, амперметр, источник тока (батарея элементов), ключ, соединительные провода.

МЕТОДИКА ИЗМЕРЕНИЙ

Все постоянные магниты, к которым относятся и магнитные стрелки, обладают двумя разноимёнными полюсами: северным и южным. Одноимённые полюсы взаимно отталкиваются, а разноимённые полюсы взаимно притягиваются. Помещая магнитные стрелки в различные точки Земли, можно сделать вывод о существовании магнитного поля Земли. Магнитные полюсы Земного шара не совпадают с географическими полюсами: рядом с северным географическим полюсом находится южный магнитный полюс и наоборот. Это магнитное поле создаётся довольно устойчивыми вихревыми электрическими токами, протекающими внутри земного шара. Силовой характеристикой магнитного поля является вектор магнитной индукции В. Величина и направление вектора магнитной индукции могут быть установлены с помощью витка с током (пробного контура).

Магнитный момент pm витка с током определяется как произведение

где n - единичный вектор нормали к плоскости контура. Направление n и pm

определяется правилом правого винта: если вращать правый винт по

3

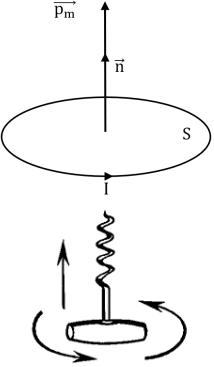
направлению тока, то поступательное движение винта укажет направление магнитного момента (рис.1).

На плоский замкнутый контур с током, помещённый в магнитное поле,

действует момент сил M, модуль которого равен: M = pmB sin α, где α - угол между векторами m и . Из этой формулы следует: модуль вектора магнитной индукции в данной точке магнитного поля равен наибольшему значению момента сил Mmax, действующего на рамку с током, имеющую единичный по модулю магнитный момент pm и помещённую в окрестность данной точки:

Рис. 1. Плоский замкнутый контур с током

Значение M = Mmax соответствует такой ориентации рамки, при которой , т.е. линии магнитной индукции лежат в плоскости рамки, а её магнитный момент направлен перпендикулярно к линиям индукции.

4

За единицу 1 Тл (Тесла) принимается, в соответствии с законом Ампера и формулой 2, величина индукции такого поля, для которого Mmax= 1Н∙м, сила тока I в пробном контуре равна 1 А, а площадь контура с током S равна 1м2.

Из соотношения (2) следует, что

1 [Тл] = 1 [Ам∙∙мН2] = 1 [АДж∙ м2] = 1 [Вм∙2с].

Для графического изображения магнитного поля вводятся линии

индукции вектора B, имеющие вид замкнутых кривых (рис.3). Замкнутость

линий магнитной индукции означает, что в природе отсутствуют свободные магнитные заряды.

Раскрыв векторное произведение, получаем значение модуля вектора dB:

правилу векторного произведения I|dl, r| (правило «буравчика»), а б.

5

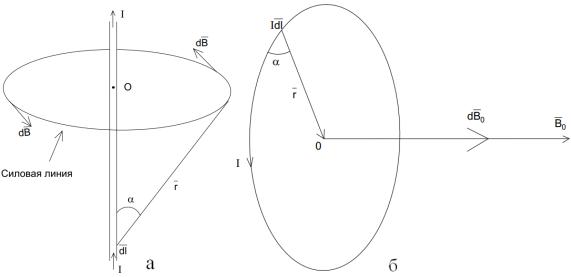
Рис. 2. Магнитное поле:

а − прямолинейного проводника с током;

б − кругового проводника с током

Поле в любой точке пространства является суперпозицией полей,

создаваемых элементами тока всего проводника. Из рис. 2 б следует, что в

(I)(I)

Ввоздухе для точки О: µ=1; r = R, α = 90°; I = const; l меняется от 0 до 2πR .

Подстановка этих значений в (4) даёт

6

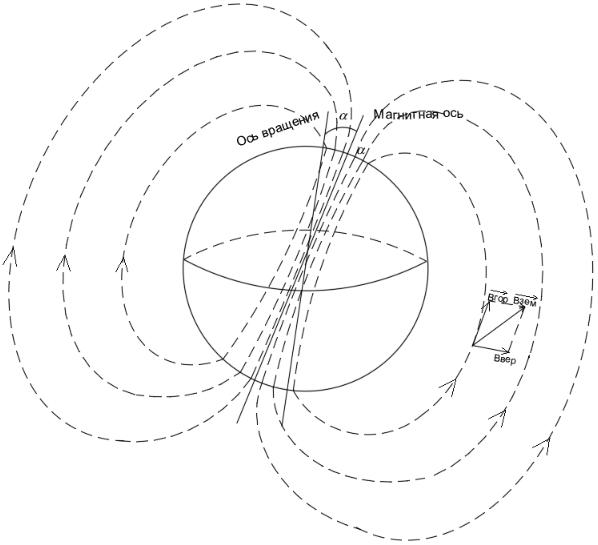
Рис. 3. Силовые линии геомагнитного поля

Величина индукции геомагнитного поля Bзем зависит от широты местности, изменяясь в пределах (0,42 + 0,70) ∙ 10−4Тл . Более высокие значения Bзем могут быть в районах магнитных аномалий. Направлен вектор

Bзем в сторону северного конца свободно подвешенной магнитной стрелки, т.е.

силовые линии вектора Bзем выходят из Южного полушария Земли и входят в Северное полушарие. Вертикальная плоскость, проходящая через магнитную стрелку, называется плоскостью магнитного меридиана, а линия пересечения этой плоскости с поверхностью Земли − магнитным меридианом. Магнитные меридианы не совпадают с географическими, так как в настоящее время ось геомагнитного поля отклонена от оси вращения Земли на угол α ≈ 11,5°.

7

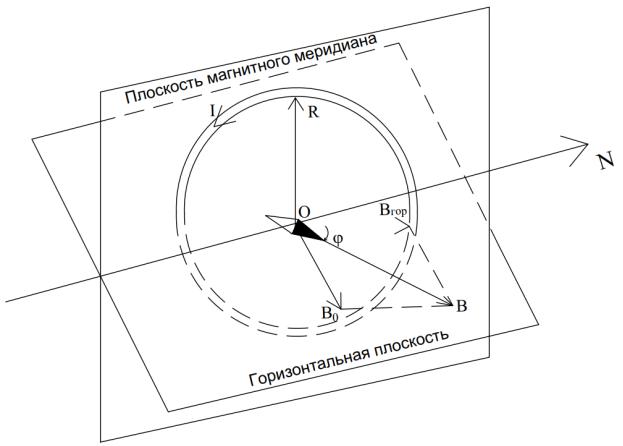
Горизонтальной составляющей Bгор вектора индукции магнитного поля Земли называется проекция вектора Bзем на касательную (горизонталь) к

магнитному меридиану. Величину Bгор можно измерить с помощью тангенс-

гальванометра (рис. 4), представляющего собой круговой контур с током, в

центре которого находится магнитная стрелка на вертикальной оси (компас).

Тангенс-гальванометр позволяет сравнивать Bгор с индукцией магнитного поля

B0, создаваемого током, протекающим по контуру. Для этого контур в отсутствии тока устанавливают в плоскости магнитного меридиана по магнитной стрелке. После включения тока в контуре на стрелку действует

Рис. 4. Схема тангенс-гальванометра

8

Угол φ отсчитывается по шкале тангенс-гальванометра. Для усиления магнитного поля тангенс-гальванометра его круговой контур, по которому течёт ток I, делают из нескольких (n) витков одинакового радиуса R. Индукция поля на оси такой катушки увеличивается в n раз:

При подстановке (7) в (6) получается

Из выражения (8) следует, что сила тока в контуре определяется по величине тангенса угла отклонения магнитной стрелки:

Так как в определённой точке Земли Bгор величина постоянная, то для данного прибора в данной местности коэффициент пропорциональности C = const и

называется постоянной тангенс-гальванометра. Из формулы (9) можно установить физический смысл постоянной С: она равна силе тока,

отклоняющего стрелку тангенс-гальванометра на угол φ = π4. Из рис. 4 видно,

что в этом случае B0 = Bгор. Таким образом, постоянная тангенс-гальванометра равна силе тока, создающего в центре контура магнитное поле, индукция которого по величине равна Bгор.

Измеряя углы отклонения магнитной стрелки при известных значениях силы тока в контуре, можно найти постоянную тангенс-гальванометра:

Определив постоянную С, можно использовать тангенс-гальванометр в качес-

тве амперметра.

Для нахождения величины Bгор формула (10) подставляется в (8):

9

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

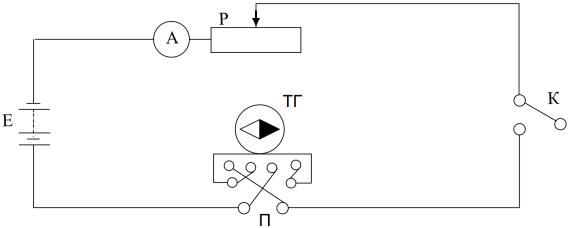
1. Соберите цепь по схеме на рис. 5, где Е - источник тока; Р – реостат;

А – амперметр; К – ключ; П – переключатель; ТГ – тангенс-

гальванометр.

Рис. 5. Схема установки

2.Определите необходимые для расчёта Bгор табличные данные и парамет-

ры тангенс-гальванометра и внесите их в табл. 1.

3.Установите круговой контур тангенс-гальванометра в плоскости магнит-

ного меридиана по магнитной стрелке.

4.На реостате Р установите максимальное сопротивление и замкните цепь ключом К. Уменьшая сопротивление реостата, подберите такой ток, при котором угол отклонения ≈ 45°.

5.Найдите углы отклонения стрелки для 3-7 значений силы тока и внесите данные в табл. 2. При изменении тока угол φ должен быть в пределах

30 ÷ 60° . Для уменьшения влияния погрешностей установки тангенс-

10

гальванометра измерение каждого угла φ проводите по обоим концам стрелки (С, Ю) и при разных направлениях тока, коммутируемого переключателем П (φлев, φправ). Среднее значение угла вычисляется по формуле

6.Определите абсолютные погрешности измеряемых и табличных величин

(∆μ0, ∆n, ∆R, ∆I, ∆φср) и внесите их в табл. 1 и 2.

ОБРАБОТКА ДАННЫХ И ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ

1.Найдите значение tgφ и по формуле (10) вычислите постоянную тангенс-гальванометра для каждого опыта; найдите среднее значение

Сср.

2.Вычислите относительные и абсолютные погрешности постоянной

тангенс-гальванометра по формулам

3.В формулу (11) подставьте данные из строки «среднее» табл. 1 и 2 и

вычислите горизонтальную составляющую индукции магнитного поля Земли Bгор .

11

СОДЕРЖАНИЕ ОТЧЁТА

1.Краткая теория с расчётными формулами.

2.Схема установки и перечень приборов и принадлежностей.

3.Таблица с результатами измерений.

4.Расчёты величин С и Вгор и их погрешностей.

5.Результаты расчётов в стандартном виде.

6.Выводы по работе.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Расскажите о порядке выполнения работы.

2.Объясните физический смысл индукции магнитного поля B. В каких единицах она измеряется?

3.Как найти направление и модуль магнитного момента витка с током?

Как связаны между собой магнитный момент и момент сил,

действующий на плоский замкнутый контур с током, помещённый в магнитное поле?

4.Запишите закон Био-Савара-Лапласа. Какие величины входят в этот закон? Как применять этот закон для определения величины и направления индукции магнитного поля в данной точке?

5.Выведите формулу индукции магнитного поля в центре кругового тока.

Нарисуйте силовые линии поля B кругового тока.

12