
Лабораторные работы / ЛР 16 Определение универсальной газовой постоянной
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра физики и биомедицинской техники
ОПРЕДЕЛЕНИЕ УНИВЕРСАЛЬНОЙ ГАЗОВОЙ ПОСТОЯННОЙ, МОЛЯРНОЙ МАССЫ И ПЛОТНОСТИ ВОЗДУХА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
клабораторной работе № 16 по дисциплине «Физика»
Составители: В.Г. Пыльнев, С.Е. Строковская
Липецк Липецкий государственный технический университет
2016
УДК 539.1 (07)
П 947
Составители: В.Г.Пыльнев, С.Е.Строковская
Рецензент – Г.С.Строковский, канд. техн. наук
Определение универсальной газовой постоянной, молярной массы и плотности воздуха [Текст]: методические указания к лабораторной работе № 16 по дисциплине «Физика» / В.Г.Пыльнев,С.Е.Строковская – Липецк: Издво Липецкого государственного технического университета, 2016. – 11 с.
В методических указаниях представлена лабораторная работа по изучению способа определения универсальной газовой постоянной, плотности воздуха и молярной массы воздуха.
Предназначены для студентов 1-го и 2-го курсов всех технических специальностей.
Табл. 1 . Ил. 1 . Библиогр.: 3 назв.
© ФГОБУ ВО «Липецкий государственный технический университет», 2016

ЛАБОРАТОРНАЯ РАБОТА № 16
ОПРЕДЕЛЕНИЕ УНИВЕРСАЛЬНОЙ ГАЗОВОЙ ПОСТОЯННОЙ,
МОЛЯРНОЙ МАССЫ И ПЛОТНОСТИ ВОЗДУХА
Цель работы:
Изучение законов идеального и реального газа, экспериментальное определение универсальной газовой постоянной, молярной массы и плотности воздуха.
Приборы и принадлежности:
Баллон; насос - «груша»; манометр; зажим; соединительные шланги; барометр;
термометр.
Краткая теория
Идеальный газ – это модель реального газа, удовлетворяющая следующим условиям: а) размерами молекул можно пренебречь по сравнению с расстоянием между ними, то есть молекулы идеального газа считаются материальными точками; б) молекулы идеального газа не взаимодействуют на расстоянии, то есть между ними отсутствуют силы притяжения или отталкивания; в) взаимодействие молекул со стенками сосуда происходит по законам абсолютно упругого удара. Воздух можно считать идеальным газом при давлении Р ≤ 100 кПа и температуре Т ≥ 270 К.
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) устанавливает связь между параметрами состояния газа, то есть объемом V, давлением Р, абсолютной температурой Т и массой М:
= |
|
, |
(1) |
|
где μ – масса одного моля газа ( или молярная масса); R – универсальная газовая постоянная.
Физический смысл R получим из уравнения состояния (1) для одного моля (М = μ)
3
|
= . |
(2) |
|
|
|
Если нагреть 1 моль газа на ∆ = 1 К в изобарном процессе ( Р = const), то его
объем увеличится на ∆ |
и уравнение состояния будет иметь вид: |
|
( |
+ ∆ ) = ( + ∆ ) = ( + 1) . |
(3) |
|
|
|
Вычитая из уравнения (3) уравнение (2), получим: |
|
|
|
∆ = , |
(4) |
где ∆ = – это работа газа.
Таким образом, универсальная газовая постоянная равна работе,
совершаемой одним молем идеального газа при изобарном нагревании на 1 К.
Молярная масса вещества определяется по формуле
|
= ∙ , |
(5) |
|
|
|
где - масса одной молекулы (атома) данного вещества;
= 6,02∙1023 моль−1 - число Авогадро, равное числу молекул (атомов) в 1
моле вещества.
Для воздуха, являющегося смесью газов, молярная масса вычисляется по
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
= |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(6) |
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где: – масса i-го газа в смеси; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
− число молей i-го газа в смеси. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательная формула для массы моля смеси газов |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
+ + + |
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
2 + + |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислить μ |
для воздуха, состоящего из 78 % молекул азота |
|
|
( |
2 |
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
= 28∙10−3 кг/моль), 21 % кислорода |
|
( |
2 |
= 32∙10−3 |
кг/моль) |
и |
1 % |
Ar |
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
( = 40∙10−3 кг/ моль), можно, предположив, что общая масса воздуха
4

∑ = 100 г, а масса каждого газа (в граммах) равна его содержанию в воздухе в процентах.
Плотность ρ равна массе единицы объема вещества
|
|
|
|
||
= |
|
|
. |
(8) |
|
|
|
||||
Для идеального газа плотность можно найти из уравнения состояния (1) |
|
||||
|
|
|
|||
= |
|
. |
(9) |
||
|
|||||
Из (9) очевидно, что плотность воздуха, как и любого газа, зависит от давления Р и температуры Т. При нормальных условиях (Рн.у. ≈ 101,3 кПа; Тн.у. ≈
273,2 К) для воздуха н.у. ≈ 1,29 мкг3.
При проведении опытов с реальным газом на результаты могут влиять размеры молекул газа и взаимодействия между ними. Поэтому для реального газа вместо уравнения состояния (2) вводится уравнение Ван-дер-Ваальса:
( + ⁄ 2) ∙ ( |
− ) = , |
(10) |
|
|
|
где а – постоянная, учитывающая силы притяжения между молекулами (силы Ван-дер-Ваальса); b – постоянная, учитывающая размеры (объем) молекул, (а и b – это табличные величины, полученные из опыта для данного газа.)
При откачке воздуха из сосуда, то есть при его адиабатическом расширении, молекулы удаляются друг от друга и совершают работу против сил притяжения за счет уменьшения кинетической энергии ср. Так как ср
пропорциональна температуре газа Т, то при откачке (расширении) газа происходит понижение его температуры (эффект Джоуля – Томсона). Этот эффект часто наблюдается в виде обмерзания отверстия в баллоне, из которого выпускают сильно сжатый газ (кислород, азот). После прекращения откачки газ в закрытом баллоне изохорно нагревается до комнатной температуры и его давление увеличивается.
5
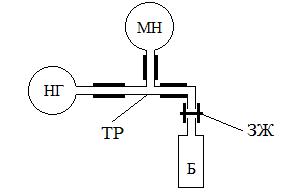
Методика измерений
Экспериментальная установка (Рис.1) состоит из баллона Б, манометра МН, насоса – «груши» НГ, тройника ТР, шлангов и зажима ЗЖ.
Рис.1. Экспериментальная установка Для нахождения универсальной газовой постоянной определяют все
остальные величины, входящие в уравнение (1). Эксперимент проводится при постоянной комнатной температуре Т и постоянном объеме б баллона Б. В
опытах необходимо определить массу воздуха М и его давление Р в баллоне.
Чтобы не находить массу воздуха М отдельно от массы баллона Мб, можно
определить суммарные массы М1б |
и М2б газа и баллона Б при двух разных |
|||
давлениях Р1 и Р2. Запишем уравнение (1) для двух состояний газа: |
|
|||
1 б = 1/ |
(11) |
|||
2 б = 2/ . |
(12) |
|||
Вычитая из уравнения (12) уравнение (11), получим: |
|
|||
= |
б(2 − 1) |
. |
(13) |
|
|
||||
|
( |
− ) |
|
|
2 |
1 |
|
|
|
Так как 1 = 1б − б, а 2 = 2б − б, то 2 − 1 = 2б − 1б. |
(14) |
|||
Подставляя (14) в (13), получим расчетную формулу для вычисления универсальной газовой постоянной
= |
б(2 − 1) |
. |
(15) |
||
|
|||||
|
( |
− |
) |
|
|
|
2б |
1б |
|
|
|
6
Упражнение 1
Измерение универсальной газовой постоянной
1.Запишите в отчет значения постоянных и табличных величин, необходимых для расчетов по формуле (15), а также для сравнения с полученными в работе результатами: объем баллона б; давление
атмосферы ; комнатную температуру |
= (0 + 273) ; молярную |
|||||
ат |
|
|
|
комн |
|
|
массу воздуха |
|
= 29 ∙ 10−3 |
кг/моль; |
универсальную |
газовую |
|
табл |
|
|
|
|
|
|
постоянную = 8,31 |
|
Дж |
. (По указанию преподавателя |
найдите |
||
|
|
|||||
|
моль∙К |
|
табл |
|
||
|
|
|
|
|||
по формуле (7)).
2.Подготовьте таблицу для записи прямых измерений и погрешностей остальных величин, входящих в расчетную формулу (15).
|
|
|
|
|
|
|
|
|
|
Таблица |
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
1 |
∆1 |
1б |
∆1б |
2 |
∆2 |
2б |
∆2б |
изм |
∆изм |
|
опыта |
|
|
|
|
|
|
|
|
|
|
|
кПа |
кг |
кПа |
кг |
Дж/(моль∙К) |
|
||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сред- |
|
|
|
|
|
|
|
|
|
|
|
нее |
|
|
|
|
|
|
|
|
|
|
|
3.Отсоединив баллон Б от тройника, определите суммарную массу 1б
баллона, зажима, шланга и воздуха в баллоне при атмосферном давлении
ат = 1. Занесите значения 1б и 1 в таблицу измерений.
4.Соединив баллон с тройником, насосом –«грушей» накачайте воздух в баллон и закройте зажимом шланг, соединяющий баллон с тройником. Спустя 2 – 3 минуты после накачки, когда температура воздуха в баллоне сравняется с температурой в лаборатории, запишите в таблицу давление
2.
7
5.Отсоедините баллон Б со шлангом и зажимом, определите новую массу
2б и занесите ее в таблицу.
6.Проделайте пункты 3, 4, 5 несколько раз, вычислите по формуле (15) и
занесите в таблицу для каждого опыта значения универсальной газовой постоянной и найдите среднее значение изм.
7.Определите абсолютные погрешности для измеренных и табличных величин и вычислите для одного из опытов относительную погрешность
по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∆ |
= |
∆ |
+ |
∆б |
+ |
∆1 + ∆2 |
+ |
∆ |
+ |
∆2б + ∆1б |
. |
(16) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
б |
|
1 + 2 |
|
|
|
2б + 1б |
|
|
|
|
|
|
|
|
|
|||||||
8.Определите абсолютную погрешность ∆.
9.Запишите величины изм и табл в стандартном виде и представьте их на числовой оси.
Упражнение 2
Измерение молярной массы воздуха
1.Молярную массу воздуха можно определить по расчетной формуле,
полученной из (15):
µ = |
(2б − 1б) |
. |
(17) |
|
|
||||
|
( |
− ) |
|
|
|
2 |
1 |
|
|
Запишите в отчет значения постоянных и табличных величин, входящих в формулу (17): б, атм, комн, , табл. (По указанию преподавателятабл найдите по формуле (7)).
2.Подготовьте таблицу прямых измерений (как в Упражнении 1, заменив
изм и изм на изм и изм .)
3.Выполните измерения по пунктам 3, 4, 5, 6 из Упражнения 1, вычислите по формуле (17) для каждого опыта значения молярной массы и
найдите среднее значение изм.
8

7.Определите абсолютные погрешности для измеренных и табличных величин и вычислите для одного из опытов относительную погрешность
µ по формуле |
|
|
|
|
|
|
|
|
|
|
|||
= |
∆ |
= |
∆ |
+ |
∆б |
+ |
∆2 + ∆1 |
+ |
∆ |
+ |
∆2б + ∆1б |
. |
(18) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
б |
|
2 + 1 |
|
|
|
2б + 1б |
|
|
|
|
|
|
|
|
|
|||||||
8.Определите абсолютную погрешность ∆.
9.Запишите величины изм и табл в стандартном виде и представьте их на числовой оси.
Упражнение 3
Измерение плотности воздуха
1.Плотность воздуха можно определить по расчетной формуле (9).
Запишите в отчет значения постоянных и табличных величин, входящих
в (9): давление атмосферы атм; комнатную температуру комн= ( 0 + 273)К; универсальную газовую постоянную = 8,31 Дж/(моль ∙ К);
плотность воздуха при нормальных условиях н.у. = 1,29 мкг3.
2.Вычислите молярную массу воздуха по формуле (7).
3.Определите плотность воздуха лаб в лабораторных условиях по формуле
(9).
4.Определите абсолютные погрешности для измеренных и табличных
величин и вычислите относительную погрешность лаб
= |
∆ |
= |
∆ |
+ |
∆ |
+ |
∆ |
+ |
∆ |
. |
(19) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5.Определите абсолютную погрешность ∆лаб по формуле (19), запишите величины лаб и н.у. в стандартной форме и представьте их на числовой оси.
6.Сравните значение плотности воздуха лаб, полученное в лабораторных условиях, с плотностью в нормальных условиях н.у. и объясните разницу.
9
Содержание отчета
1.Цель работы.
2.Перечень приборов и схема установки.
3.Краткая теория с расчетными формулами.
4.Таблица с экспериментальными данными.
5.Вычисление значений , , по расчетным формулам.
6.Вычисление погрешностей ∆ , ∆ , ∆.
7.Результаты расчетов в стандартной форме и на числовой оси.
8.Выводы по работе.
Контрольные вопросы
1.Что такое идеальный газ? В каких условиях реальный газ можно считать идеальным?
2.Сформулируйте газовые законы.
3.Сравните уравнения состояния для идеального газа и газа Ван-дер-
Ваальса.
4.Каков физический смысл универсальной газовой постоянной?
5.Что такое молярная масса и как ее определить для смеси газов (воздуха)?
6.Почему давление в баллоне изменяется в течение некоторого времени после отключения насоса?
7.Запишите первое начало термодинамики для различных изопроцессов.
8.Запишите формулы работы газа при всех изопроцессах.
9.Напишите и объясните формулы внутренней энергии для идеального и
реального газов.
10.Как определить плотность газа? Как плотность газа зависит от его
давления и температуры?
10
