
Лабораторные работы / ЛР 1 Измерение плотности твердого тела
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Липецкий государственный технический университет»
Кафедра физики и биомедицинской техники
ИЗМЕРЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе № 1
по дисциплине «Физика»
Утверждаю к печати |
Первый проректор ЛГТУ |
Объем п.л. |
Качановский Ю.П. |
Тираж 100 экз. |
«____» __________ 2015 г. |
Липецк Липецкий государственный технический университет
2015
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Липецкий государственный технический университет»
Кафедра физики и биомедицинской техники
ИЗМЕРЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе № 1
по дисциплине «Физика»
Составители: В.Г.Пыльнев, С.Е.Строковская, Т.А.Герасименко, Г.М.Кавыгина
Рукопись утверждаю |
Зав. кафедрой физики и БМТ |
|
Шарапов С.И. |
|
«____» ____________ 2015г. |
Липецк Липецкий государственный технический университет
2015
ЛАБОРАТОРНАЯ РАБОТА № 1
ИЗМЕРЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
Цели работы:
1.Изучить правила измерения физических величин.
2.Освоить методы оценки погрешностей измерения.
3.Приобрести практические навыки работы с измерительным инструментами:
штангенциркулем, микрометром, техническими весами.
Приборы и принадлежности:
Штангенциркуль, микрометр, технические весы, металлическое тело
цилиндрической формы.
I. Правила измерения физических величин, определения их
погрешностей и оформления результатов на примере плотности
металлического тела
Неизвестную физическую величину можно измерить, то есть сравнить с величиной, принятой за единицу, двумя способами:
а) прямым измерением, определяя значение непосредственно с помощью соответствующего прибора, например, измерение длины стержня линейкой или определение массы тела путем взвешивания на весах;
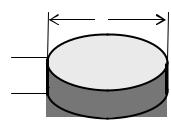
б) косвенным измерением, определяя значение искомой величины по результатам прямых измерений других величин. Например, плотность тела можно найти по формуле (1), пользуясь результатами прямых измерений массы m и размеров тела (рис. 1):
3
|
m |
|
4m |
, |
(1) |
|
V |
d 2 h |
|||||
|
|
|
|
где |
V |
d 2 h |
|
4 |
|||
|
|
- объем тела.
d
h 
Рис. 1. Измеряемое тело (образец)
Общие правила проведения прямых и косвенных измерений содержатся в «Методических рекомендациях к лабораторному практикуму» [1].
а) Прямые измерения
1. Для определения плотности тела по формуле (1) необходимо подготовить таблицу и заполнить ее по результатам измерений (в таблице внесены условные данные в качестве примера).
|
|
|
|
|
|
|
|
|
|
|
|
Таблица |
|
|
Результаты прямых измерений величин и их погрешности |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
m |
|
m |
d |
|
d |
h |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
мм |
|
мм |
- |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
63,25 |
|
0,01 |
25,01 |
|
0,03 |
18 |
|
0,5 |
3,14 |
|
0,005 |
|
2 |
63,12 |
|
0,14 |
25,05 |
|
0,01 |
18 |
|
- |
- |
|
- |
|
3 |
63,41 |
|
0,15 |
25,06 |
|
0,02 |
18 |
|
- |
- |
|
- |
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
- |
|
- |
- |
|
- |
- |
|
- |
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср |
63,26 |
|
0,10 |
25,04 |
|
0,02 |
18 |
|
0,5 |
3,14 |
|
0,005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СИ |
|
кг 10 3 |
|
м 10 3 |
|
м 10 3 |
- |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
ср |
63,26 |
|
0,10 |
25,04 |
|
0,02 |
18 |
|
0,5 |
3,14 |
|
0,005 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
0,00158 0,16% |
0,0008 0,08% |
0,0277 2,77% |
0,0016 0,16% |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
Количество столбцов в таблице равно количеству величин в формуле (1) (
m, d, h, ) с учетом их погрешностей ( m, d, h, ) .

2.Анализ данных из таблицы показывает, что измеренные значения массы m
идиаметра d образца меняются при многократных измерениях. Следовательно,
эти величины имеют случайную погрешность, которая определяется по формулам, которые даны в «Методических рекомендациях к лабораторному практикуму по общей физике» [1]. Сначала находим средние значения mc p и dcp
:
|
|
|
mcp |
m1 m2 m3 |
|
|
63,25 63,12 63,41 |
63,26 |
г . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
dcp |
|
d1 d2 d3 |
|
25,01 25,05 25,06 |
25,04 |
мм . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Затем находим погрешности отдельных измерений mi , di |
и средние значения |
|||||||||||||||||||||||||||
абсолютных погрешностей mcp и dcp : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
; |
|
di |
|
di |
|
. |
|
|
|
(3) |
|||||||||
|
|
|
|
|
|
mi |
mcp mi |
|
|
dcp |
|
|
|
|
||||||||||||||
|
|
mcp |
m1 m2 m3 ; |
|
dcp d1 |
d2 d3 |
. |
(4) |
||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||
Подставляя числа из табл.1 в формулы (3) и (4), получим: |
|
|
|
|
||||||||||||||||||||||||
m |
|
|
0,01 0,14 0,15 |
0,10 г ; |
d |
|
|
0,03 0,01 0,02 |
0,02 |
мм . |
||||||||||||||||||
cp |
|
|
|
|
cp |
|
||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. При многократных измерениях менее точными приборами (например, |
||||||||||||||||||||||||||||
линейкой вместо штангенциркуля) |
измеренные значения |
не |
изменяются ( |
|||||||||||||||||||||||||
h1 h2 h3 ). |
В этом |
случае измеренная |
величина |
|
h имеет |
систематическую |
||||||||||||||||||||||
погрешность большую, чем случайная.. Такую погрешность обычно принимают равной половине приборной погрешности, которую в лабораторных работах можно считать равной цене наименьшего деления шкалы ( a ). Для линейки a = 1
мм, поэтому hcp a 1мм 0,5мм .
2 2
5 4. Если величина, входящая в расчетную формулу, в данной работе не
измеряется, а берется из справочника или описания установки (например, ),

то в таблице записывают округленное значение этой величины ( 3,14).
Абсолютную погрешность округленной табличной величины обычно принимают равной половине единицы последнего не нулевого десятичного
разряда. В нашем примере: 0,01 0,005 .
2
5. Округление измеренных и табличных величин делают так, чтобы
сохранялась примерно равная точность всех величин, входящих в расчетную
формулу (1). Точность измерения разных величин нельзя сравнивать по абсолютным погрешностям, которые имеют разную размерность и порядок значений. Для сравнения точности измерений или вычислений определяют относительные погрешности для всех величин (без размерности или в %).
m |
|
|
|
mcp |
|
|
|
0,10 |
|
|
0,00158 0,16% ; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
mcp |
|
|
63,26 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
d |
|
|
dcp |
|
|
0,02 |
|
|
0,0008 0,08% ; |
|
(5) |
||||||||||||||||
|
|
dcp |
|
|
|
25,04 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
h |
hcp |
|
|
|
0,5 |
|
0,0277 2,8% ; |
|
|
||||||||||||||||
|
|
|
hcp |
|
|
|
18 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
cp |
|
|
|
|
0,005 |
|
0,016 0,16% . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3,14 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Полученные значения |
заносят в нижнюю строку таблицы. |
|
|
||||||||||||||||||||||||
Очевидно, что высота h измерена менее точно, так как h d |
m . |
|
|||||||||||||||||||||||||
Для повышения точности величины |
hcp необходимо уменьшить абсолютную |
||||||||||||||||||||||||||
погрешность hcp , что достигается заменой грубого прибора (линейка, |
a 1мм ) |
||||||||||||||||||||||||||
на более точный (штангенциркуль, a 0,05мм или a 0,02мм ). |
|
|
|||||||||||||||||||||||||
б) Косвенные измерения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Среднее значение плотности cp вычисляют, подставляя средние значения прямых измерений массы mc p , размеров dcp и
6
величину из таблицы (в единицах СИ).
в формулу (1) hcp и табличную

cp |
|
4mcp |
|
|
4 63,26 10 3 |
7140 |
кг |
7,140 |
10 |
3 |
кг |
. |
(6) |
||
d |
2 |
h |
|
(25,04 10 3 )2 18 10 3 |
м3 |
|
м3 |
||||||||
|
|
3,14 |
|
|
|
|
|
|
|||||||
|
|
|
cp |
cp |
|
|
|
|
|
|
|
|
|
|
|
Определим погрешность косвенного измерения изложенными в «Методических рекомендациях по общей физике» [1].
1. Найдем натуральный логарифм формулы (1):
cp в соответствии с правилами,
к лабораторному практикуму
|
|
ln ln 4 ln m ln 2ln d ln h . |
|
||||||||||||
2. |
Найдем полный дифференциал (по всем переменным): |
|
|||||||||||||
|
|
d |
0 |
d (m) |
|
d ( ) |
|
2 |
d (d ) |
|
d (h) |
. |
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
m |
|
|
d |
|
h |
|
||||||
3. |
Заменим знак дифференциала d на знак абсолютной погрешности , а |
|
|||||||||||||
все знаки «-» перед абсолютными погрешностями на знаки «+»: |
|
||||||||||||||
|
|
|
|
m |
|
2 d |
h . |
(7) |
|||||||
|
|
|
|
m |
|
|
d |
|
h |
|
|||||
Замена знаков «-» на «+» делается для получения максимально возможной погрешности при случайном сложении погрешностей прямых измерений.
4. Подставляем средние значения измеренных величин и погрешностей из таблицы в формулу (7) и вычисляем относительную погрешность косвенного измерения плотности
|
cp |
|
mcp |
|
cp |
2 |
dcp |
|
hcp |
|
|
|
|
2 |
|
|
|
(8) |
||||||
|
|
|
|
|
|
|
m |
|
d |
h |
||||||||||||||
|
|
cp |
|
mcp cp |
|
dcp |
hcp |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
cp |
0,00158 0,0016 2 0,0008 0,0277 0,03248 3,25%. |
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
cp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. По найденному значению найдем абсолютную погрешность cp : |
|
|||||||||||||||||||||||
cp cp 7140 0,03248 231,91 |
кг |
0,23191 103 |
|
кг |
. |
|
(9) |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
м3 |
|
|
|
|
м3 |
|
|
|||||
6. Округляем cp , оставляя одну ненулевую значащую цифру (или две, если первая цифра – единица)
7
cp 0,23191 103 мкг3 0,2 103 мкг3 .

7. Округляем cp , оставляя все верные цифры и одну сомнительную.
Сомнительными считаются цифры в последних разрядах cp , начиная с разряда,
использованного при округлении cp :
cp 7,140 103 мкг3 7,1 103 мкг3 .
в) Оформление и анализ результатов измерений.
1. Полученные значения плотности стандартной форме:
cp и ее погрешности записываем в
( |
|
|
|
) |
кг |
(7,1 0,2)103 |
кг |
; |
|
|
3,25%. |
(10) |
|||
cp |
cp |
м |
3 |
м |
3 |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Для определения материала исследованного образца выберем из справочных таблиц плотности разных металлов, близкие по величине к измеренной нами плотности:
Сталь (железо): |
Fe |
(7880 5) |
|
кг |
|
(7,880 0,005) 103 |
|
кг |
|
|||||||
|
м3 |
|
|
м3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Чугун: |
чуг |
(7000 500) |
|
|
кг |
(7,0 0,5) 103 |
кг |
|
|
|||||||
|
|
|
м3 |
|
||||||||||||
|
|
|
|
|
|
|
м3 |
|
||||||||
Цинк: |
Zn |
(7150 5) |
|
кг |
|
(7,150 0,005) 103 |
|
кг |
|
|
||||||
м3 |
|
|
м3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Олово: |
Sn |
(7290 5) |
|
кг |
|
. (7,290 0,005) 103 |
|
кг |
|
|||||||
|
м3 |
|
м3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Сравнение плотностей металлов удобнее и нагляднее делать в графическом виде на числовой оси. Для определения масштаба оси (цены деления) находим максимальное и минимальное значения плотностей выбранных металлов (с
учетом погрешностей), которые должны поместиться на оси :
max Femax (7,880 0,005) 103 |
кг |
7,885 103 |
кг |
, |
|||||
м3 |
м3 |
||||||||
|
|
|
|
|
|
||||
min Чугmin (7,0 0,5) 103 |
кг |
6,5 103 |
кг |
. |
|
||||
|
|
|
|||||||
|
м3 |
|
м3 |
|
|||||
8

4. Изобразим на графике (рис.2.) измеренную плотность тела (снизу оси) и
табличные плотности металлов (сверху оси) с интервалами их погрешностей.
Рис. 2.
Графическое сравнение экспериментальной и табличной величин плотности материала образца
5. Интервалы погрешностей на графике перекрываются с интервалами для
Zn , Sn и чуг . Очевидно, условный образец не может быть из чистого железа,
так как интервал для Fe на оси не совпадает с интервалом .
6. Окончательный вывод о материале образца можно сделать по его цвету и механическим свойствам. Наиболее вероятным в данном случае является сплав на основе железа (чугун), имеющий широкий диапазон плотностей и высокую твердость по сравнению с цинком и оловом.
II.Устройство измерительных приборов и порядок выполнения
измерений
а) Измерительные приборы
Штангенциркуль применяют для измерения линейных размеров тел с большей точностью, чем по миллиметровой линейке. Штангенциркулем можно измерять внешний размер, внутренний размер и глубину.
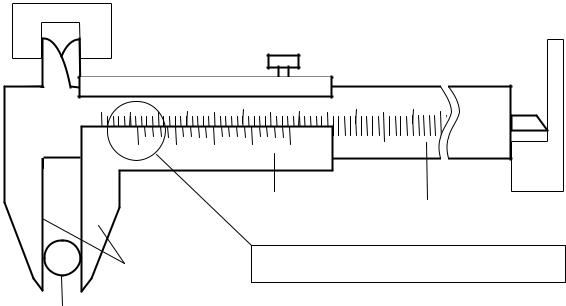
Основные части штангенциркуля (рис. 3): штанга со шкалой Ш,
измерительные губки, нониус. Нониус – это вспомогательная шкала, которая нанесена на подвижную губку и перемещается вместе с ней вдоль штанги с основной шкалой Ш. Длина деления нониуса l2 делается меньше длины деления основной шкалы 11 на величину а = 11 – 12, которая называется точностью нониуса и обычно указывается на штангенциркуле (на рис.3 а = 0,05 мм).
9
Измерение |
|
Фиксирующий |
|
|
|||
внутреннего |
|
|
|
||||
|
|
винт |
|
Измерение |
|||
|
размера |
|
|
|
|||
|
|
|
|
|
|
глубины |
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
3 |
4 |
5 |
6 |
0 |
25 |
50 |
|
75 |
1 |
а = 0,05 мм |
|
|
|
|
|||||
|
|
|
|
Нониус |
|
Штанга со |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шкалой Ш |
Измерительные |
Размер, измеренный на рисунке – 6,10 мм |
||||||
|
губки |
|
|
||||
|
|
|
|
|
|
|
|
Измеряемое
тело
Рис. 3. Штангенциркуль
При смещении нулевого деления нониуса вправо относительно некоторого
деления основной шкалы на х = а совпадет первое деление нониуса со
следующим делением основной шкалы. При смещении нулевого деления на х = 2а совпадут вторые деления, при х = n·а совпадут n-ые деления.
Таким образом, зная точность нониуса а и номер совпавших делений n,
можно определить величину смещения начала нониуса х в пределах основной шкалы. Если нуль нониуса смещен на N целых делений основной шкалы и еще
на часть следующего деления, то x = N+n·a. |
(11) |
Порядок измерения линейного размера тела штангенциркулем:
1)зажать тело между измерительными губками;
2)определить число целых делений основной шкалы N;
3)определить номер наименьшего деления нониуса n, совпадающего с одним из делений основной шкалы;
4)вычислить измеряемый размер по формуле (11).
Приборную погрешность штангенциркуля можно считать равной точности
нониуса (систематическая погрешность измерения равна половине приборной
погрешности).
10
