3.6. Виды графов
и
операции над ними
3.6.1. Некоторые специальные виды графов
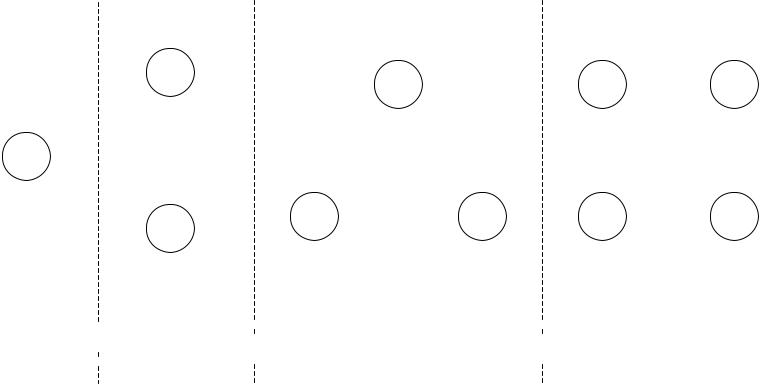
Пустой граф G – граф, в котором отсутствуют ребра. On – пустой граф порядка n
Пример
1 |
2 |
2 |
3 |
|
1
2 |
1 |
3 |
1 |
4 |
|
|
|
|
О1 |
|
О2 |
|
О3 |
|
О4 |
|
|
|
||||
|
||||||
|
||||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
Полный граф G – граф, в котором любые две его вершины смежны.
Kn – полный граф порядка n
Число ребер: m | EG | n(n 1) 2
Пример
1 |
2 |
2 |
3 |
|
1
2 |
1 |
3 |
1 |
4 |
|
|
|
|
К1 |
К2 |
К3 |
К4 |
Граф G(V, E) называется двудольным, если множество его
вершин можно разбить так, что V V1 V2, V1 V2 Ø.
При этом каждое ребро e E соединяет вершины из разных множеств.
Пример.
1 |
1 |
2 |
2
3 |
3 |
4 |
4
5 |
5 |
6 |
|
Граф G(V, E) называется полным двудольным, если любая вершина из одной доли смежны со всеми вершинными из другой доли. Обозначение: Kn1,n2 , если |V1 | n1, |V2 | n2.
Пример.
1 |
1 |
2 |
2
3 |
3 |
4 |
4
5 |
5 |
6 |
|
К3, 2 |
К3,3 |
Реберный граф
Для произвольного графа G реберный граф L(G) определяется двумя условиями:
1)VL(G) EG
2)вершины e1 и е2 смежны в L(G) тогда и только тогда, когда ребра e1 и е2 смежны в G.
Пример.
G |
2 |
L(G) |
е1 |
е2 |
1 |
е1 |
|
|
3 |
|
|
|
|
|
е6 |
е3 |
||
|
|
е4 |
е3 |
|
||
е2 |
|
е5 |
|
|
||
|
|
|
|
|
||
|
5 |
е6 |
|
4 |
е5 |
е4 |
|
|
|
|
Проверка:
A(L(G)) IT (G) I(G) 2E
Пример.
G |
|
е3 |
|
2 |
3 |
||
|
|||
|
е1 |
е4 |
|
1 |
|
е5 |
|
|
|
||
|
е2 |
е6 |
|
|
4 |
||
|
5 |
|
|
|
e1 e2 e3 e4 |
e5 e6 |
|
||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|||
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
||||||||
I(G) |
3 |
0 0 1 |
1 |
1 |
1 |
|
|||
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
4 |
|
||||||||
|
5 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
|
||||||||
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|||
|
1 |
0 |
0 |
0 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
||
A(L(G)) 0 1 |
1 |
0 |
0 |
|
0 |
|
2E |
||||||||
|
0 |
0 |
1 |
1 |
1 |
1 |
|
||||||||
|
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
||||
|
0 0 1 |
1 |
0 |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
2
1110
0
1 |
1 |
1 |
0 |
0 |
|
2 |
0 |
0 |
0 |
1 |
|
0 |
2 |
2 |
1 |
|
|
1 |
|
||||
0 |
2 |
2 |
1 |
1 |
|
0 |
1 |
1 |
2 |
|
|
1 |
|
||||
1 |
1 |
1 |
1 |
|
|
2 |
|
|
|
e1 e2 e3 e4 e5 e6 |
|
||||||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
0 |
1 |
1 |
1 |
0 |
0 |
||
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
|
e2 |
|
|
|||||||
2E e |
|
1 |
0 |
0 |
2 |
1 |
1 |
|
|
3 |
|
1 |
0 |
2 |
0 |
1 |
1 |
|
|
e4 |
|
|
|||||||
e |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
|
|
e6 |
|
|
|||||||
Пример.
G |
е1 |
е3 |
|
1 |
2 |
||
|
е2 |
е4 |
е1 |
е3 |
|
|
3
L(G)
е2 е4
Проверку выполнить самостоятельно!!!