Тема 2. Отношения и функции
2.1. Отношения
Упорядоченная пара (x, y) - это совокупность, состоящая из
двух элементов х и у, расположенных в определенном поряд- ке.
Две пары (x, y) и (u, v) считаются равными x = u, y = v.
Бинарным (двуместным) отношением ρ называется множе- ство упорядоченных пар.
Обозначение:
или |
|
(x, y) ρ |
|
|
|
x ρ y. |
|
|
|
|
|
|
|
|
Область |
определения |
бинарного |
отношения |
ρ |
D {x | y, |
x y}. |
|
|
|
Область |
значений |
бинарного |
отношения |
ρ |
R {y | x, |
x y}. |
|
|
|
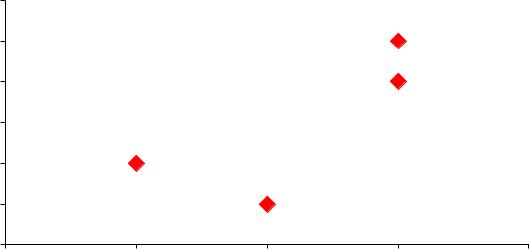
Пример.
1. Множество {(1, 2),(2, 1),(3, 4),(3, 5)} – бинарное отношение. Его графическое изображение
6 |
|
|
|
|
|
5 |
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
2. {(x, y) | x, y R, x y} - отношение равенства, |
|||||
где D |
R |
R - множество действительных чисел. |
|||
Для задания отношений на конечных множествах обычно
используют матрицы отношений.
Матрица бинарного отношения на множестве А = {a1, a2, …, |
||||||||||||||||||
am} - квадратная матрица С порядка т с элементами |
||||||||||||||||||
|
|
|
1, |
|
если |
|
ai aj , |
|
|
|
|
|
|
|
|
|
||
сij |
|
иначе |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. На множестве А={1,2,3,4,5} |
|
|
||||||||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
|||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|||||
|
2 |
|
0 |
1 |
1 |
1 |
|
|
|
2 |
|
0 |
1 |
0 |
0 |
|
|
|
|
|
1 |
|
|
0 |
|||||||||||||
|
3 |
|
0 |
0 |
1 |
1 |
1 |
|
3 |
|
0 |
0 |
1 |
0 |
0 |
|||
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
0 0 0 1 |
|
|
|||
4 |
|
1 |
4 |
|
0 |
|||||||||||||
|
5 |
|
0 |
0 |
0 |
0 |
|
|
|
5 |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
1 |
|
|
1 |
|||||||||||||
Прямым произведением множеств X и Y называется совокуп-
ность всех упорядоченных пар (x, y) таких, что x X, y Y .
Обозначение X Y .
Пример.
1. Пусть Х = {2, 3, 5}, Y = {1, 3}. Тогда
X×Y = {(2, 1), (2, 3), (3, 1), (3, 3), (5, 1), (5, 3)} Y×X = {(1, 2), (1, 3), (1, 5), (3, 2), (3, 3), (3, 5)}
При этом X×Y Y×X
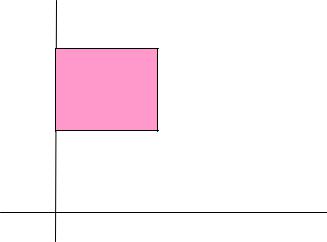
2. Пусть X [0,1],Y [1,2]. Тогда X Y [0,1] [1,2] Графически
Y
2
1
1 X
Обратным отношением для отношения называется отно-
шение
1 {(x, y) | ( y, x) }
или
1 {( y, x) | (x, y) }
Композицией отношений 1 и 2 называется отношение
|
|
2 1 {(x, y) | z,(x, z) 1 и |
(z, y) 2} |
||
Свойства |
|
|
|
||
1. 1 1 . |
|
|
|||
2. |
2 |
1 |
1 |
1 |
|
|
1 |
1 |
2 |
|
|
2.2. Функции и отображения
Бинарное |
отношение |
f называется функцией, если из |
(x, y) f |
и (x, z) f |
следует, что y z. |
Две функции равны, если они состоят из одних и тех же элементов.
Область определения функции Df и область значений
функции Rf определяются также как и для бинарного отношения.
Если Df X и Rf Y , то говорят, что функция f задана на
множестве Х со значениями во множестве Y и осуществляет отображение множества Х во множество Y. Другими словами, устанавливает соответствие между множествами
Х и Y.
Это отображение обозначается следующим образом: f : X Y .
Если f – функция, то записывают y f (x) и говорят, что у –
значение, соответствующее аргументу х, или у – образ элемента х при отображении f. При этом х называют
прообразом элемента у.
Пример.
Отношение
{(x, x2 3x 2) | x R}
является функцией.
Возможна и следующая запись
y x2 3x 2.
2.3. СПЕЦИАЛЬНЫЕ БИНАРНЫЕ ОТНОШЕНИЯ
ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
ОТНОШЕНИЕ ПОРЯДКА