Електричні машини_К3С2(6) / Іспит / Літ / voldek_ai_elektricheskie_mashiny / Глава 21

Глава двадцать первая

ОБМОТКИ ПЕРЕМЕННОГО ТОКА

§ 21-1. Трехфазные двухслойные обмотки с целым числом пазов на полюс и фазу

Общие сведения о трехфазных обмотках. Обмотки переменного тока подразделяются на однослойные и двухслойные.

В современных машинах переменного тока применяются преимущественно двухслойные обмотки.

В двухслойных обмотках, как и в якорных обмотках машин постоянного тока (см. гл. 3), стороны катушек лежат в пазах в два слоя и каждая катушка одной стороной лежит в верхнем, а другой стороной — в нижнем слое. При этом все катушки имеют одинаковые размеры и форму. Широкое применение двухслойных обмоток объясняется следующими их преимуществами: 1) возможностью укорочения шага на любое число зубцовых делений, что выгодно с точки зрения подавления высших гармоник э.д.с. и н.с. обмоток (см. § 20-3 и 22-1) и уменьшения расхода обмоточного провода; 2) одинаковыми размерами и формами всех катушек, что упрощает и облегчает изготовление обмоток; 3) относительно простой формой лобовых частей катушек (см. рис. 19-20), что также упрощает изготовление обмотки.

Как и якорные обмотки машин постоянного тока, двухслойные обмотки переменного тока делятся на петлевые и волновые, которые в электромагнитном отношении равноценны. Преимущественно применяются петлевые обмотки. Волновые же обмотки используются обычно при числе витков в катушке .

В подавляющем большинстве случаев применяются трехфазные обмотки с фазной зоной , и поэтому мы ограничимся рассмотрением этих обмоток. После изучения таких обмоток нетрудно составить также, если это потребуется, схемы обмоток с зоной .

Обмотки могут иметь как целое, так и дробное число пазов на полюс и фазу q [(см. равенство 20-24)]. В последнем случае обмотки называются дробными.

Петлевые обмотки с целым числом пазов на полюс и фазу. В кaчестве примера рассмотрим обмотку с Z = 24 и 2р = 4. Тогда

и величина полюсного деления, выраженная в зубцовых делениях,

Выберем шаг обмотки у = 5 зубцовых делений. Тогда относительный шаг

Схема этой обмотки при последовательном соединении всех катушечных групп фазы изображена на рис. 21-1, причем для большей

Рис. 21-1. Схема трехфазной двухслойной петлевой обмотки с Z = 24,

m = 3, 2р = 4, q = 2, у = 5,

наглядности разные фазы показаны линиями разного характера. Порядок составления схемы рис. 21-1 можно пояснить следующим образом.

Сначала распределяем верхние стороны катушек (пазов) по фазным зонам по q = 2 стороны (пазов) в каждой зоне. Если пазы 1 и 2 отвести для зоны фазы A, то зоне фазы В нужно отвести пазы 5 и 6, так как фаза В должна быть сдвинута относительно фазы A на 120°, т.е. на две зоны по 60° или на 4 паза (1+4 = 5; 2 + 4 = 6). Зона С сдвинута относительно зоны В также на 120° и занимает пазы 5 + 4 = 9 и 6 + 4 = 10. На протяжении следующего двойного полюсного деления (пазы 13—24) чередование зон А, В и С происходит с такой же закономерностью (зона A — пазы 13, 14; зона В — пазы 17, 18; зона С — пазы 21, 22). Таким образом, распределена половина фазных зон и пазов верхнего слоя. Другие фазные зоны также распределяем по фазам A, В, С и обозначаем их соответственно X, Y, Z. При этом для зон X, принадлежащих фазе A, отводим пазы, которые сдвинуты относительно зон A на = 6 пазов, т.е. пазы 1+6 = 7, 2 + 6 = 8, 13 + 6 = 19, 14 + 6 = 20. Аналогично зонам Y принадлежат пазы 5 + 6 = 11, 6 + 6 = 12, 17 + 6 = 23, 18 + 6 = 24, а зонам Z — пазы 9 — 6 = 3, 10 — 6 = 4, 21 — 6 = 15, 22 — 6 = 16. Различие между зонами A, В, С и X, Y, Z состоит в том, что э.д.с. в соответствующих сторонах катушек (например, катушек зон А и X) сдвинуты по фазе на 180° вследствие их сдвига в магнитном поле на одно или нечетное число полюсных делений.

В результате получим распределение верхних сторон катушек (пазов) по фазным зонам, изображенное в верхнем ряду верхней части рис. 21-1.

Поскольку в рассматриваемом случае шаг укорочен на одно зубцовое деление, то нижние стороны катушек (пазов) будут сдвинуты на одно зубцовое деление влево, как это изображено в нижнем ряду верхней части рис. 21-1. Отметим, что распределение нижних сторон по зонам можно и не производить, так как оно получится автоматически при вычерчивании лобовых соединений катушек.

Весьма важно отметить, что полученное на рис. 21-1 чередование фазных зон A, Z, В, Х, С, Y с q пазами в каждой зоне, повторяющееся на протяжении каждого двойного полюсного деления, характерно для любой трехфазной обмотки с фазной зоной = 60° и поэтому нет надобности производить каждый раз приведенные выше расчеты.

Распределение пазов по фазам можно произвести также на основании звезды пазовых э.д.с. обмотки (рис. 21-2).

Р ис 21-2 Звезда пазовых э.д.с. обмотки, изображенной на рис 21-1

Сдвиг э.д.с. проводников соседних пазов по фазе

(21-1)

В рассматриваемом случае , как изображено на рис. 21-2, а. После обхода векторов пазовых э.д.с. на протяжении двух полюсных делений (в нашем случае векторы 1 — 12) звезда векторов э.д.с. при целом q будет повторяться вследствие совпадения э.д.с. соответствующих пазов (1 и 1 + 12 = 13 и т.д.) по фазе. Если отвести первые два вектора (рис. 21-1) для зоны А (векторы 1; 2 и 13 и 14), то векторы зон В и С будут сдвинуты от векторов А на 120° и 240°. Векторы зон X, Y, Z будут сдвинуты относительно векторов зон А, В, С соответственно на 180°. В результате получим такое же распределение пазов по зонам, как показано в верхнем ряду на рис. 21-1.

На схеме рис. 21-1 для каждого паза начерчены два проводника (стороны катушки) Будем считать, что левые из них расположены в верхних слоях, а правые — в нижних. Катушки будем нумеровать по верхним сторонам. Так как э.д.с. соседних катушек тоже сдвинуты на , то звезду э.д.с. пазов (рис. 21-2) можно рассматривать и как звезду э.д.с. катушек.

В пределах каждой катушечной группы q = 2 катушки соединяются последовательно. Таким образом, для фазы А на рис. 21-1 получим четыре группы, состоящие соответственно из катушек 1—2, 7—8, а) 13—14 и 19—20. Все они соединены последовательно, причем группы 7—8 и 19—20 «вывернуты» по отношению к группам 1—2 и 13—14 (конец группы 1—2 соединен с концом же группы 7—8 и т.д.), чтобы э.д.с. всех групп складывались друг с другом. Аналогично произведено соединение групп в других фазах.

Включение катушечных групп зон X, Y, Z в цепь обмотки во встречном направлении эквивалентно повороту векторов э.д.с. катушек этих зон на 180°. При этом вместо рис. 21-2, а получим диаграмму э.д.с. катушек, изображенную на рис. 21-2, б, состоящую из трех секторов, в каждом из которых имеется q = 2 луча и 2pq = 2 · 2 · 2 = 8 векторов соответственно числу катушек в фазе. Э.д.с. каждой фазы равна сумме векторов э.д.с. катушек соответствующего сектора. Очевидно, что э.д.с. всех фаз будут равны и сдвинуты по фазе на 120°.

В качестве начал фаз A, В и С на рис. 21-1 взяты начала катушек 1, 5 и 9 со сдвигом на 120°. Концы фаз X, Y, Z на рис. 21-1 соответствуют началам катушек 19, 23 и 3. Начала и концы фаз можно взять также иначе. Например, на рис. 21-1 можно соединить концы фаз А и X, разрезать затем любое междугрупповое соединение фазы А и полученные концы взять за начала и концы фазы А.

Ч исло катушечных групп в каждой фазе двухслойной обмотки с фазной зоной = 60° равно числу полюсов 2р. Э.д.с. всех групп равны по величине, а с учетом «вывертывания» катушечных групп Х, Y, Z совпадают также по фазе. Поэтому в двухслойной обмотке с целым q можно выполнить до совершенно равноценных параллельных ветвей, в которых индуктируются э.д.с, одинаковые по величине и совпадающие по фазе. Например, в рассматриваемом случае (2р = 4) обмотку можно выполнить с или 4 (рис. 21-3) параллельными

Рис. 21-3. Схемы соединений для фазы А

обмотки, изображенной на рис. 21-1, при

выполнении а = 2 и а = 4 параллельных

ветвей

ветвями. Стрелками на рис. 21-3 указаны направления токов параллельных ветвей.

Волновые обмотки с целым числом пазов на полюс и фазу. В мощных машинах переменного тока, в частности в крупных турбо- и гидрогенераторах, вследствие большого магнитного потока и большого количества катушек необходимое напряжение обмотки статора достигается при числе витков в катушке . В этом случае двухслойная обмотка имеет в каждом пазу только два проводника или стержня большого сечения, из которых образованы витки путем пайки в лобовых частях. Такие обмотки называются стержневыми и применяются также в качестве фазных обмоток роторов асинхронных двигателей средней и большой мощности. В последнем случае обмотка выполняется из массивных медных стержней, чем достигается лучшее использование площади паза за счет уменьшения объема изоляционных материалов в пазу. Возможность применения таких обмоток для роторов асинхронных двигателей облегчается тем, что эти обмотки не соединяются с сетью и поэтому не должны быть рассчитаны на стандартные напряжения. Кроме того, лобовые части стержневой обмотки являются более жесткими и не имеют междувитковой изоляции, вследствие чего их крепление против действия центробежных сил облегчается.

Стержневые обмотки можно выполнять как петлевыми, так и волновыми. Однако в большинстве случаев при 2р > 2 их делают волновыми, так как при этом за счет уменьшения соединений между катушечными группами (см. рис. 21-1) достигается экономия меди и уменьшение трудоемкости изготовления обмотки. Эта экономия особенно ощутима в многополюсных машинах, например в гидрогенераторах.

Схема трехфазной двухслойной стержневой волновой обмотки с теми же данными, что на рис. 21-1, изображена на рис. 21-4.

Р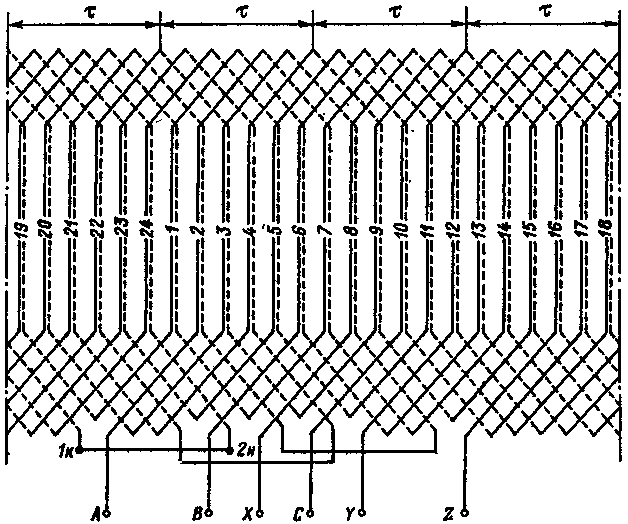 ис. 21-4. Схема трехфазной двухслойной волновой обмотки с Z = 24,

m = 3, 2р = 4, q = 2, у = 5,

Распределение пазов по фазным зонам производится аналогично, и это распределение такое же, как и на рис. 21-1, а звезда пазовых э.д.с. такая же, как на рис. 21-2. Для удобства обозрения схемы счет пазов на рис. 21-4 начат с отступлением от левого края, т.е. чертеж схемы обмотки как бы разрезан в другом месте по сравнению с рис. 21-1.

Начало фазы А на схеме рис. 21-4 взято из верхнего слоя паза 2. При обходе этой фазы от ее начала А обойдем виток 2, лежащий своей верхней стороной в пазу 2, из конца витка 2 (нижний слой паза 7) перейдем в виток 14 и в конце этого витка (нижний слой паза 19) завершим полный обход вокруг якоря. При этом в общем случае будет обойдено р (в данном случае р = 2) витков. Второй обход вокруг якоря начинается с соединения конца витка 14 с началом витка 1. Это соединение короче (6 зубцовых делений), чем другие соединения (например, соединение между катушками 2 и 14, имеющее 7 зубцовых делений). При втором обходе якоря пройдем еще р = 2 катушки (1-ю и 13-ю) и закончим этот обход выходом из нижней стороны паза 18 (конец 1к на рис. 3-4). В данном случае, при q = 2, этим заканчивается первый цикл обходов вокруг якоря. При q = 3 и 4 и т.д. этот цикл включает 3; 4 и т.д. обходов, причем будет использовано pq витков (катушек) обмотки (в данном случае 2 · 2 = 4 витка), т.е. половина всех 2pq витков (катушек) фазы.

Второй цикл обходов фазы А на схеме рис. 21-4 начат (конец 2н) из нижней стороны катушки 19 (нижняя сторона паза 24), при этом в данном случае все витки фазы соединены последовательно перемычкой 1к2н. Второй цикл обходов совершается в противоположном направлении, причем q = 2 обхода охватывают катушки 20, 8, 19, 7 и заканчиваются концом фазы X. Аналогично выполнены соединения в фазах В и С. Независимо от числа полюсов обмотка будет иметь три перемычки, соединяющие циклы обходов в каждой фазе.

Таким образом, каждая фаза волновой обмотки состоит из двух половинок по pq катушек в каждой. Эти половинки можно соединить также параллельно, и, следовательно, волновая обмотка может иметь удобно выполняемые параллельные ветви.

Укорочение шага в волновой обмотке в электромагнитном отношении дает такой же эффект, как и в петлевой обмотке. Э.д.с. и обмоточные коэффициенты обеих обмоток вычисляются по общим формулам (см. гл. 20).

Укорочение шага в волновой обмотке в отличие от петлевой обмотки не приводит к уменьшению расхода проводникового материала на лобовые соединения, так как при этом соединения с одной стороны машины укорачиваются, а с другой удлиняются. Волновые обмотки роторов асинхронных двигателей чаще всего выполняют с полным шагом ( ), а начала А, В, С и концы Х, Y, Z обмотки распределяют равномерно по окружности с целью облегчения балансировки (уравновешивания масс) ротора,

§ 21-2. Трехфазные двухслойные обмотки с дробным числом пазов на полюс и фазу

Общие положения. При производстве асинхронных двигателей на разные числа пар полюсов р в целях экономии на изготовлении штампов иногда используются одинаковые вырубки листов стали статора или ротора, с одинаковым числом пазов Z. Если при этом для одних двигателей число пазов на полюс и фазу

(21-2)

получается целым, то для других это число будет дробным, и в них применяются дробные обмотки. Дробные обмотки используются и в ряде других случаев, например в мощных тихоходных гидрогенераторах, у которых полюсное деление относительно мало, а пазы ввиду большого сечения проводников должны быть достаточно большими. При этом число пазов на полюс mq, а также q получаются малыми. В данном случае для улучшения формы кривой э.д.с. вместо целого, но малого q целесообразно взять хотя бы также малое, но дробное q. Благоприятная форма кривой э.д.с. дробной обмотки объясняется следующим.

Как было выяснено в § 20-3, для гармоник магнитного поля порядка

(21-3)

коэффициенты укорочения шага и распределения равны значениям этих коэффициентов для основной гармоники и , так как сдвиги э.д.с. по фазе от этих гармоник поля для проводников различных пазов одинаковы. Поэтому обмотка с целым q не подавляет гармоник э.д.с. индуктируемых такими гармониками поля возбуждения. Более того, под влиянием пазов эти гармоники э.д.с. даже усиливаются.

При целом q значения v_z [см. выражение (21-3)] представляют собой нечетные целые числа и в кривой поля возбуждения содержатся гармоники поля таких же порядков. Для дробных обмоток значения v_z не будут целыми нечетными числами. Так, например, при для трехфазной обмотки (т = 3) получим , и т.д. Числа v_z будут целыми нечетными только при больших значениях k, и при этом они также будут большими. В случае дробной обмотки э.д.с. от гармоник поля v = 1 и v = v_z для проводников различных пазов также имеют одинаковый сдвиг фаз, как это следует из равенства (20-36). Поэтому при дробном q для гармоник порядка v_z имеем , и обмотка не подавляет э.д.с. от этих гармоник. Однако при дробном q поле возбуждения не содержит дробных гармоник v_z, определяемых равенством (21-3), и поэтому не возникает вопроса о подавлении э.д.с. от этих гармоник. В то же время для целых нечетных гармоник, содержащихся в поле возбуждения, сдвиг фаз между э.д.с. проводников соседних пазов для основной гармоники

и для высших гармоник (v = 5, 7, 11, 13...)

при дробной обмотке различен. Например, при m = 3 и имеем для основной гармоники

и для гармоник v = 5, 7, 11, 13, 17 соответственно . Поэтому в контурах витков, катушек и катушечных групп векторы этих гармоник э.д.с. складываются под различными углами сдвига фаз, вследствие чего происходит подавление э.д.с. от высших гармоник поля возбуждения v = 5, 7, 11, 13, 17... В данном случае ( ) лишь при k = 5 формула (21-3) определяет гармоники порядков

содержащиеся в поле возбуждения. Для этих гармоник , но амплитуды этих гармоник поля весьма малы и индуктируемые ими э.д.с. незначительны.

Общие свойства дробных обмоток. Рассмотрим характерные особенности дробных обмоток.

Дробное число q можно представить в виде

(21-4)

где b, с и d — целые числа, с < d и является несократимой правильной дробью. Часть катушечных групп имеет по b катушек, а другая часть — по b + 1 катушек. При этом из каждых d групп катушек d — с групп должны иметь по b катушек, а с групп — по b + 1 катушек. Эти d групп содержат тогда

(d – c) b + c ( b+l ) = bd + c

катушек, и среднее число катушек в группе

что и соответствует равенству (21-4).

Таким образом, общее число катушек дробной обмотки должно быть всегда равно или кратно bd + с, а общее число катушечных групп должно быть равно или кратко d, ибо в противном случае равенство (21-4) соблюдаться не будет. Ширина фазной зоны при дробном q соблюдается только в среднем.

Каждая фаза двухслойной обмотки содержит 2р катушечных групп. Каждая из фаз по условиям симметрии должна иметь по одинаковому количеству малых (по b катушек) и больших (по b + 1 катушек) катушечных групп. Поэтому, согласно сказанному, в каждой фазе должно быть малых и больших катушечных групп. Так как эти числа должны быть целыми и и представляют собой несократимые дроби, то очевидно, что

(21-5)

т.е. 2р должно быть кратно или равно d и d ≤ 2р.

Можно показать, что для образования симметричной трехфазной обмотки наряду с соблюдением равенства (21-5) необходимо, чтобы

(21-6)

Минимальное число пазов

при котором возможно выполнение симметричной трехфазной обмотки, равно при нечетном d

Z' = 6(bd + c), (21-7)

а при четном d

Z' = 3(bd + c). (21-8)

Минимальное число полюсов для образования симметричной трехфазной обмотки 2р равно при нечетном d

2p' = 2d. (21-9)

и при четном d

2p' = d. (21-10)

В общем случае полное число полюсов 2р может быть кратным 2р', т.е.

2р=2p't, (21-11)

и тогда звезда э.дс. всей обмотки будет представлять собой t наложенных друг на друга звезд с z' лучами в каждой. В этом случае обмотка в целом состоит из t одинаковых частей, из которых каждая занимает по окружности 2р' полюсов и охватывает Z' катушек. При этом можно образовать а = t одинаковых параллельных ветвей по d катушечных групп с bd + с катушками в каждой ветви.

С хема симметричной дробной обмотки (рис. 21-5) может иметь ряд

Рис. 21-5 Схема трехфазной двухслойной петлевой дробной обмотки с Z = 30,

2р = 8, , a = 2, у = 3, = 0,8

вариантов. Одним из них будет такой, который дает максимальную э.д.с. Для этого большие и малые катушечные группы нужно распределить симметрично или равномерно по окружности. Такое распределение называется максимальным, и только оно рассматривается ниже.

Звезду пазовых э.д.с. дробной обмотки (рис. 21-6, а) можно

Рис. 21-6 Звезда пазовых э.д.с. обмотки, изображенной на рис. 21-5

рассматривать и как звезду э.д.с катушек. Катушки фазных зон X, Y, Z, лежащие под противоположными полюсами по сравнению с катушками зон A, В, С, включаются в последовательную цепь обмотки встречно, чтобы э.д.с всех катушечных групп фазы складывались. Это соответствует повороту векторов э.д.с. катушек зон X, Y, Z на 180°. При таком повороте этих векторов как при нечетном, так и при четном d получим три одинаковых сектора векторов, и каждый сектор занимает угол 60° по

q_э = bd+c (21-12)

лучей в каждом (рис. 3-6, б). Э.д.с. каждой фазы равна сумме векторов э.д.с. каждого сектора, и это указывает на то, что дробная обмотка по своему распределению по пазам эквивалентна обмотке с целым q, равным q_э [см. равенство (21-12)].

Поэтому q_э называется эквивалентным числом пазов дробной обмотки на полюс и фазу.

Из изложенного следует, что коэффициент распределения дробной обмотки k_р для основной гармоники надо рассчитывать по той же формуле (20-23), как и для обмотки с целым q, но с подстановкой вместо q величины q_э. Можно показать, что и для всех гармоник целого порядка (v = 1, 3, 5, 7...) коэффициенты k_рv нужно рассчитывать по формуле (20-28) с подстановкой вместо q величины q_э,

В некоторых случаях в электрических машинах существуют также такие пространственные гармоники поля, для которых отношение полюсных делений

v = τ / τ_v (21-13)

не выражается целым числом. Такие гармоники v можно назвать дробными. В частности, для дробных обмоток порядок зубцовых гармоник v_z, определяемый равенством (20-38), при d > 2 также является дробным,

Для дробных обмоток коэффициенты k_рv при дробных v вычисляются по формулам несколько более сложного вида, чем (20-28). Однако и для этих обмоток, как уже указывалось выше, для зубцовых гармоник v_z имеем k_рv = ± k_pl.

Коэффициенты укорочения шага k_yv дробных обмоток вычисляются для всех гармоник по тем же формулам, как и для обмоток с целым q.

Примеры дробных обмоток. Рассмотрим в качестве примера трехфазную двухслойную дробную обмотку с Z = 30 и 2р = 8. При этом