Електричні машини_К3С2(6) / Іспит / Літ / voldek_ai_elektricheskie_mashiny / Глава 02

Глава вторая

Магнитная цепь машины постоянноготока

при холостом ходе

§ 2-І. Метод расчета магнитной цепи

Основиым магнитным потоком Ф_δ называется поток в воздушном зазоре δ, приходящийся на один главный полюс машины.Величина Ф_δ определяет значение индуктируемой в обмотке якоря э. д. с.

При проектировании машины постоянного тока возникает необходимость определения зависимости Ф_δ от тока возбуждения полюсов. Эта задача решается путем расчета магнитной цепи машины при холостом ходе, когда ток якоря I_а = 0. Вследствие симметрии уcтройства машины и равенства потоков всех полюсов достаточно расмотреть магнитную цепь одной пары полюсов.

М агнитная цепь машины изображена на рис. 2-1, причем для

Рис. 2-1. Магнитная цепь машины по-

стоянного тока

каждого полюса штриховой линией показана такая магнитная линия потока Ф_δ, длину которой можно считать средней для всех магнитных линий.

Магнитную цепь можно рассчитать на основе закона полного тока для средней магнитной линии (рис. 2-1):

где Н — напряженность магнитного поля; dl — элемент длины магнитной линии; — полный ток, охватываемый магнитной линией.

Точное вычисление линейного интеграла (2-1) на практике затруднительно. Поэтому магнитную цепь разбивают на участки: воздушный зазор (δ), зубцы якоря (h_z), спинку якоря (L_а), полюсы

(h_m), ярмо (_Lя) и заменяют интеграл суммой, предполагая, что на протяжении каждого участка H постоянна. Тогда вместо равенства (2-1) получим

где δ, h_z, L_a, h_ω, L_я — показанные на рис. 2-1 геометрические размеры, равные длинам отрезков средней магнитной линии; H_δ, Н_z, Н_a, Н_m, H_я, — напряженности магнитного поля на соответствующих участках; ω_в, — число витков обмотки возбуждения на полюс; i_в — ток возбуждения.

Отдельные члены соотношения (2-2а) представляют собой намагничивающие силы (н. с.) отдельных участков магнитной цепи, а их сумма — полную н. с. машины на пару полюсов.

Так как для каждого участка магнитной цепи н. с. .F = Hl, то вместо (2-2а) можно также написать

(2-2б)

где F_в — полная н. с. на один полюс.

При расчете магнитной цепи, исходя из заданного значения э. д. с. Е_а и пропорциональной ей величины индукции в зазоре В_δ, определяют значения Н на отдельных участках цепи, предполагая при этом, что поток распределяется равномерно по сечениям этих участков, и затем вычисляют сумму (2-2а) или (2-2б).

Подобный приближенный расчет дает достаточную для технических целей точность. Подробности расчета магнитной цепи рассматриваются ниже. При этом расчет ведется на один полюс, т. е. вычисляется половина суммы (2-2а) или (2-2б).

§ 2-2. Магнитное поле и н.с. воздушного зазора

Гладкий якорь. Наиболее сложный характер имеет магнитное поле в воздушном зазоре, на который приходится наибольшая часть полной н. с. (до 60—80%).

Предположим сначала, что пазы на поверхности якоря и радиальные вентиляционные каналы отсутствуют.

На рис. 2-2, а показан характер магнитного поля в зазоре вдоль окружности якоря, а на рис.2-2, б — кривая 1 распределения магнитной

Р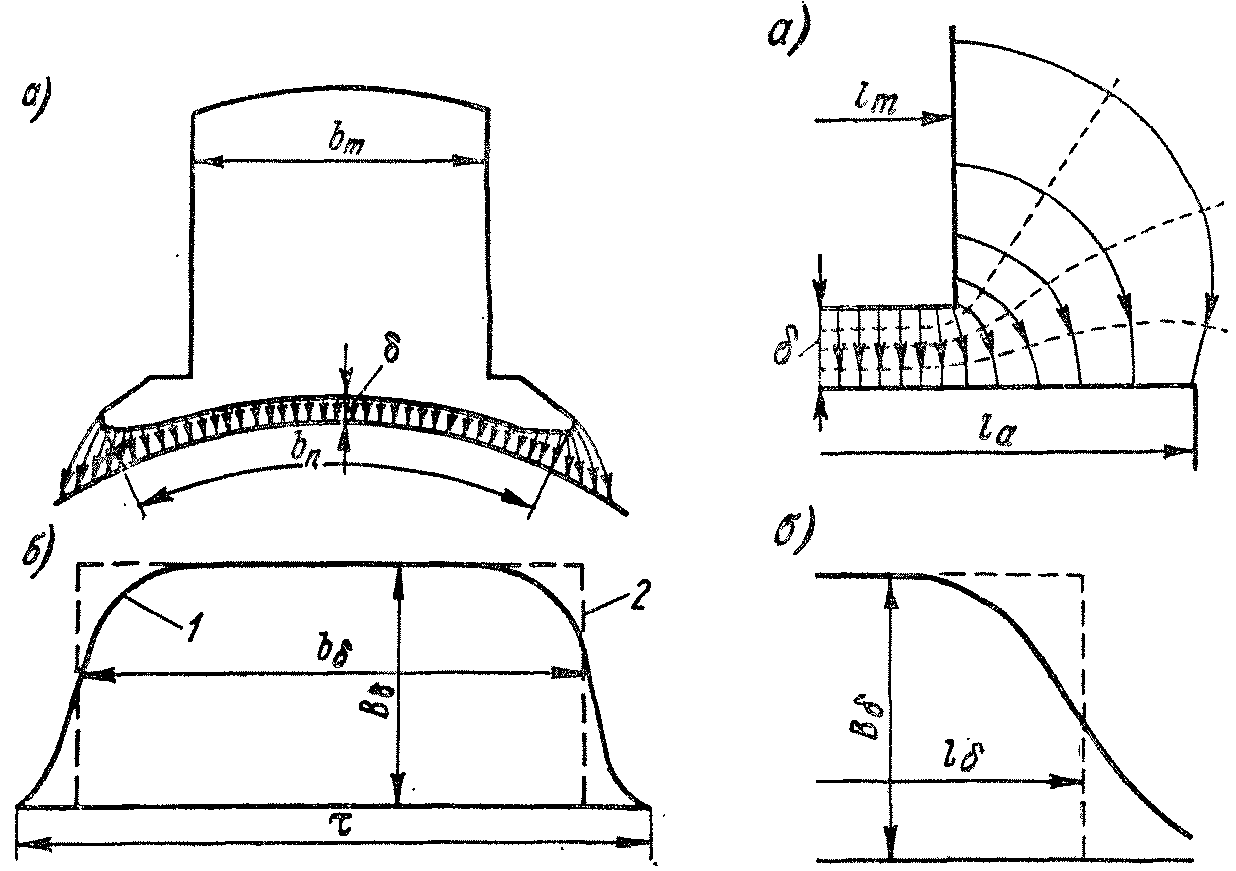 ис. 2-2. Распределение магнитной индукции в воздушном зазоре при гладком якоре

Рис. 2-3. Магнитное поле у края сердечника якоря

индукции В_δ на поверхности гладкого якоря на протяжении полюсного деления

где — внешний диаметр якоря и 2р — число полюсов.

Для расчетных целей кривую 1 заменяют прямоугольником 2 (штриховая кривая на рис. 2-2, б) шириной b_δ и высотой, равной действительному значению индукции В_δ в средней части зазора. Площадь прямоугольника равна площади фигуры, ограниченной кривой 1 и осью абсцис, что означает равенство потоков, соответствующих кривым 1и 2.

Величина b_δ называется расчетной полюсной дугой, она отличается от реальной полюсной дуги b_п (рис. 2-2, а) на некоторую величину, зависящую от формы полюсного наконечника. Точное значеиие b_δ может быть установлено путем построения картины поля в зазоре графическим методом или путем расчета . •: конформных отображений. Однако применение этих методов ввиду их большой трудоемкости каждый раз затруднительно, и поэтому пользуются приближенными соотношениями, установленными соответствующими расчетами для разных очертаний полюсных наконечников. При очертании наконечника, показанном на рис. 2-2, а,

а при равномерном зазоре δ по всей ширине наконечника

Величина

называется расчетным коэффициентом полюсной дуги. Для машин с дополнительными полюсами , и для машин без дополнительных полюсов .

Д лину якоря в осевом направлении l_a часто принимают на 5—10 мм больше длины полюсов l_m (рис. 2-3, а). При этом индукция на конце якоря

Рис. 2-2. Распределение магнитной индукции в воздушном зазоре при гладкомякоре

Рис. 2-3. Магнитное поле у края сердечника якоря

гладком якоре

ослабляется (рис. 2-3, б) и поток, входящий в торец якоря, уменьшается.

В результате уменьшаются потери на вихревые токи в нажимных фланцах и в сердечнике якоря от торцевого потока. Расчетная длина якоря в данном случае принимается равной

Таким образом, индукция в воздушном зазоре

и н. с. воздушного зазора при гладком якоре

У чет влияния пазов и вентиляционных каналов. При наличии на якоре пазов поле над ними ослабляется (рис. 2-4, а) и кривая B_δ вдоль

Рис. 2-4. Магнитное поле

в воздушном зазоре при зуб-

чатом якоре

зазора принимает зубчатый вид (рис. 2-4, б). Формула (2-4) дает значение средней индукции в зазоре B_δ, в то время как в выражение (2-5) необходимо подставить теперь значение индукции против центра зубца B_δмакс.

Отношение

называется коэффициентом воздушного зазора, обусловленным зубчатостью якоря. Значение устанавливается на основе анализа поля в зазоре и пазах методом конформных отображений. Однако получаемые при этом соотношения весьма сложные, и на практике пользуются приближенным выражением

где

B₁ − ширина открытия паза у поверхности воздушного зазора; — величина зубцового деления; Z — число зубцов якоря;

Вместо выражения (2-6) иногда пользуются также более приближенными соотношениями. Обычно

Подставив в формулу (2-5) вместо В_δ значение ,получим

Иногда пазы делают также в полюсных наконечниках, и в них размещается так называемая компенсационная обмотка (см. § 5-3). В этом случае по формулам вида (2-6) и (2-7) рассчитывается также коэффициент зазора для полюсов , причем вместо t₁ и b₁ подставляется зубцовый шаг t₂ и величина открытия паза b₂ компенсационной обмотки.

П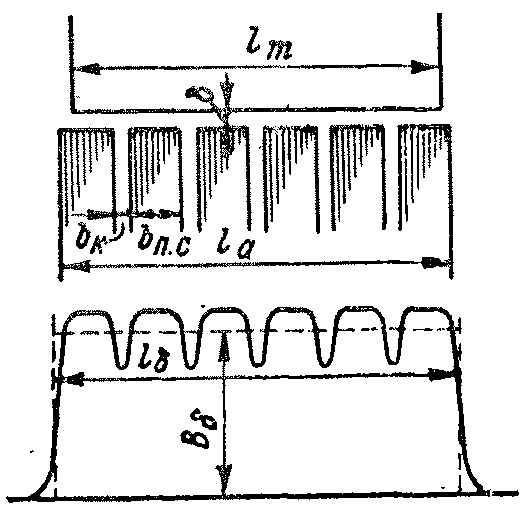 ри наличии радиальных вентиляционных каналов кривая поля вдоль зазора в осевом направлении также приобретает зубчатый характер (рис. 2-5).

Рис. 2-5. Магнитное поле в воз-

душном зазоре в осевом напра-

влении

При этом рассчитывается коэффициент зазора

где

— ширина пакета стали и — ширина вентиляционного канала.

Заметим, что иногда влияние радиальных вентиляционных каналов учитывают более приближенно, принимая в выражении (2-3) l_a равным не полной длине сердечника якоря (рис. 2-5), а суммарной ширине пакетов плюс половина суммарной ширины каналов. Коэффициент при этом рассчитывать не надо. Отметим, что расчетное значение В_δ, при этом будет несколько больше.

Учет влияния бандажных канавок. Когда обмотка якоря в пределах сердечника укрепляется бандажами, неравномерность зазора вызывается также канавками под эти бандажи. Однако учет этой неравномерности дополнительным коэффициентом зазора вида (2-6) не

Рис. 2-6. Якорь с бан-

дажными канавками

оправдан, так как этот коэффициент получен в предположении, что пазы и вентиляционные каналы глубоки, в то время как бандажные канавки неглубоки. Расчетные соотношения в этом случае можно получить следующим образом.

Если зазор в осевом направлении имеет ступенчатую форму (рис. 2-6), то относительная магнитная проводимость зазора на единицу длины дуги по окружности якоря

а в случае, когда

Отношение

определяет коэффициент уменьшения проводимости или увеличения эквивалентного зазора в результате наличия ступени с увеличенным зазором δ₂. На основе этого соотношения коэффициент увеличения эквивалентного зазора под влиянием бандажей из немагнитного материала

где — число бандажных канавок; — ширина бандажной канавки; — глубина бандажной канавки.

Когда бандажи изготовлены из магнитного материала, сечение бандажных канавок нужно уменьшить на общее сечение бандажных проволок или принять приближенно равным единице.

Заключение. Общий коэффициент воздушного зазора, как показывает анализ этого вопроса, можно рассчитать в виде произведения частичных коэффициентов зазора:

(2-12)

Тогда вместо выражения (2-8) имеем

(2-13)

При этом по-прежнему определяется равенством (2-4). Величину

в выражении (2-13) можно назвать эквивалентным воздушным зазором. Значение [см. формулу (2-12)] в машинах постоянного тока изменяется в пределах .

В расчетной практике часто выражают в Гауссах (В_δгс), а δ — в сантиметрах (δ_см). Переходя в выражении (2-13) от единиц СИ к указанным единицам, получаем

В некоторых случаях рассчитывают также н. с. на зазор небольшой величины (0,01—0,03 см) между полюсами и ярмом, который неизбежно возникает по технологическим причинам.

§ 2-3. Магнитное поле и н.с. зубцовой зоны

Следующей по сложности магнитного поля и роли ее н. с. в полной н. с. магнитной цепи является зубцовая зона. Намагничивающую силу этой зоны с достаточной для практических целей точностью можно рассчитать следующим образом.

Рассмотрим сечение зубцовой зоны на некотором расстоянии х от корня зубца (рис. 2-7).

Поток на зубцовое деление

(2-15)

Часть этого потока Ф_zx ответвляется в зубец, а остальная часть Ф_пx — в паз. Вследствие изменения геометрических соотношений

и условии насыщения соотношение между Ф_zх и Ф_пx по высоте зубца также изменяется.

Разделим равенство

Ф_t = Ф_zx + Ф_пx

на сечение зубца S_zх на расстоянии х:

(2-16)

где S_пx — площадь сечения паза на расстоянии х от корня зубца.

Левая часть равенства (2-16) представляет собой расчетную магнитную индукцию в зубце В'_zх, т. е. индукцию при Ф_пx = 0. Первое слагаемое в правой части (2-16) выражает действительную индукцию в зубце В_zх, а вместо второго члена можно написать

,

где Н_пх — напряженность магнитного поля в пазу, а

— зубцовый коэффициент, зависящий только от геометрических размеров зубцовой зоны в данном сечении.

С достаточной для практических расчетов точностью можно принять, что цилиндрические поверхности х = const на рис. 2-7 являются поверхностями уровня магнитного потенциала, которые пересекаются линиями магнитной индукции под прямым углом. Тогда Н_zх = Н_пх и вместо (2-16) получим

(2-17)

Т ак как В'_z и к_хz при заданных Ф_δ и геометрических размерах легко рассчитываются, то с помощью выражения (2-17) и заданной в графической форме кривой намагничивания материала зубцов (рис. 2-8, кривая 1) можно определить две неизвестные величины: В_zx и Н_zx.

Рис. 2-8. Определение В_z и Н_z

Для этого построим кривую 2 (рис. 2-8), прибавив к ординатам кривой 1 значения . Тогда, определив на кривой 2 точку с В'_z = В'_zx, найдем соответствующие этой точке величины и .

Если провести такой расчет для ряда сечений зубцовой зоны, то можно построить кривую (рис. 2-7) и определить н. с. зубцовой зоны:

При практических расчетах этот интеграл вычисляют приближенно, пользуясь формулой Симпсона. Тогда

(2-18)

(2-19)

а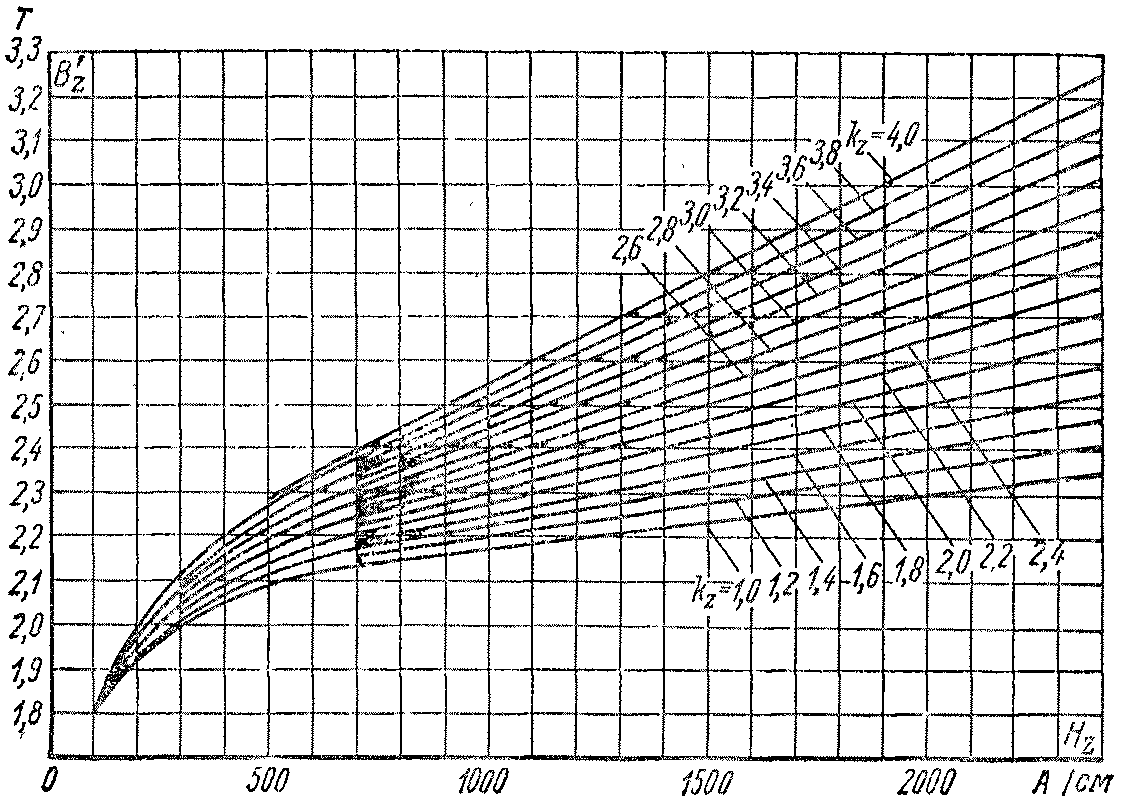 Н_z1, Н_z2, Н_z3 определяют указанным выше образом для трех сечений зубцовой зоны: верхнего 1, среднего 2 и нижнего 3 (рис. 2-7). При этом пользуются серией кривых, построенных для разных значений k_z, (рис. 2-9), и выбирают из них соответствующие данным значениям k_z1, k_z2, k_z3,

Рис. 2-9. Кривые для определения B_z.. и H_Z в зубцах из листовой

электротехнической стали марок Э11, Э12, Э21

которые определяют по формуле

(2-20)

в то время как значения В'_z1, В_z2, В'_zз вычисляют по формуле

(2-21)

В соотношениях (2-20) и (2-21) величина

l_c=l_a-n_кb_к

представляет собой суммарную длину пакетов стали и k_с — коэффициент заполнения стали (см. § В-4).

В некоторых случаях для упрощения расчетов описанным методом определяют значение на расстоянии одной третьи высоты зубца от его корня. При этом

(2-22)

Если , то зубец не насыщен и в паз ответвляется незначительная часть потока. Поэтому в данном случае можно пользоваться основной кривой намагничивания (кривая к_z = 1,0 на рис. 2-9 и кривые рис. В-1).

§ 2-4. Намагничивающие силы сердечника якоря, полюсов и ярма

Намагничивающие силы сердечника якоря, полюсов и ярма относительно малы и могут рассчитываться более приближенно.

Поток Ф_δ разветвляется в спинке сердечника якоря на две части (см. рис. 2-1), и средняя индукция в спинке

(2-23)

При наличии аксиальных вентиляционных каналов диаметром d_вент значение h_а в этой формуле уменьшают на d_вент.

Индукция по сечению спинки якоря, а также вдоль магнитной линии на рис. 2-1 несколько изменяется. Однако н. с. сердечника якоря относительно мала. Поэтому можно определить по кривым намагничивания значение Н_а, соответствующее В_а [см. формулу (2-23)], и положить

(2-24)

Значение L_а можно вычислить приближенно по следующей формуле (рис. 2-1):

(2-25)

При расчете н. с. полюса и ярма необходимо учесть, что обмотка возбуждения создает, кроме потока Ф_δ, также поток рассеяния Ф_σ, который охватывает обмотку возбуждения и проходит, минуя воздушный зазор между полюсными наконечниками и якорем, через сердечники полюсов и ярмо (рис. 2-10).

Р ис. 2-10. Поток рассеяния обмотки возбуждения между

полюсами (а) и в торцевой области (б)

Величина

(2-26)

называется коэффициентом рассеяния полюсов и может быть рассчитана по приближенным формулам [30, 40, 41], которые здесь не приводятся. В машинах постоянного тока обычно , причем большие значения относятся к многополюсным машинам с дополнительными полюсами, а меньшие — к машинам без дополнительных полюсов.

При известном значении σ определяется индукция в сердечниках главных полюсов (см. рис. 2-1, 2-5):

(2-27)

При неизолированных листах сердечника полюса

Из кривых намагничивания по В_т находятся Н_т и н. с. полюса

(2-28)

Индукция в ярме

(2-29)

где l_Я — длина ярма в осевом направлении.

Определив по В_я значение Н_я, находим

(2-30)

Длину средней магнитной линии в ярме можно вычислить по приближенной формуле (см. рис. 2-1)

(2-31)

где h_я — высота (толщина) ярма.

Выше предполагалось, что пазы в полюсных наконечниках отсутствуют. При наличии таких пазов рассчитывается также н. с. для зубцового слоя полюсных наконечников, а h_m в выражении (2-28) соответственно уменьшается.

§ 2-5. Полная намагничивающая сила и магнитная характеристика машины

Сложив вычисленные н. с. участков магнитной цепи, получим н. с. машины на один полюс.

(2-32)

причем

(2-33)

Если повторить расчет F_в для ряда значеннй основного потока Ф_δ, то можно построить (рис.2-11,кривая 1) зависимости Ф_δ = f (F_в) или Ф_δ = f=(i_в) которые отличаются только масштабом по оси абсцисс. Такие зависимости называются кривыми намагничивания или магнитными характеристиками машины.