
- •Силикаты – это соли кремниевых кислот. Они твердые тугоплавкие вещества, не имеющие окраски.
- •Общие химические свойства металлов
- •2. Реакции металлов с кислотами:
- •3. Взаимодействие металлов с водой:
- •4. Вытеснение более активными металлами менее активных металлов из растворов их солей:
- •Область применения
- •В реакциях присоединения полярных молекул типа НХ к несимметричным алкенам водород присоединяется к более гидрогенизированному атому углерода при двойной связи (т.е. атому углерода, связанному с наибольшим числом атомов водорода).
- •Реакции окисления алкенов
- •4. Окисление в присутствии солей палладия:
- •Классификация, номенклатура, изомерия
- •1. Кумулированные:
- •Номенклатура
- •2. Международная
- •В присутствии солей меди (I) и кислоты ацетилен легко димеризуется и далее тримеризуется:
- •Образование дисульфидов и их роль в биохимических процессах
- •Жиры
- •СЛОЖНЫЕ ЛИПИДЫ
- •1. Взаимодействие внутри молекулы – образование внутренних солей (биполярных ионов)
- •2. Взаимодействие с основаниями и кислотами
- •5. Качественные реакции!
- •5.1.1 Основный понятия и постулаты термодинамики
- •Исходные постулаты (положения) термодинамики. Пусть дан изолированный сосуд (рисунок 5.1.2), который разделен полупроницаемой перегородкой. В первой части сосуда температура Т1, во второй – температура Т2; Т1 > Т2.
- •5.1.2 Первый закон термодинамики, его формулировки
- •5.1.3 Термохимия
- •5.2.1 Второй закон термодинамики
- •5.2.2 Фундаментальные уравнения термодинамики
- •5.4.1 Предмет химической кинетики.
- •5.4.2 Основные понятия химической кинетики.
- •5.4.3 Кинетический закон действия масс – основной постулат химической кинетики.
- •5.4.4 Кинетические особенности протекания простых реакций.
- •5.4.5 Методы определения порядка реакции и константы скорости по экспериментальным данным.
- •5.4.6 Кинетические особенности протекания сложных реакций.
- •5.4.7 Зависимость скорости реакции от температуры.
- •5.4.8 Кинетика цепных реакций.
- •5.4.9 Кинетика фотохимических реакций.
- •5.4.10 Основы кинетики гетерогенных процессов.
- •5.4.11 Катализ.
- •5.4.1 Предмет химической кинетики
- •Химическая кинетика решает следующие задачи, перечисленные в порядке сложности их решения:
- •5.4.2 Основные понятия химической кинетики
- •АНАЛИЗ СМЕСИ АНИОНОВ
- •МЕТОДЫ КОЛИЧЕСТВЕННОГО АНАЛИЗА
- •Титриметрические методы анализа
- •Кислотно-основное титрование
- •Окислительно-восстановительное титрование
- •Перманганатометрия. Стандартизация рабочего раствора перманганата калия
- •Комплексонометрическое титрование
- •Определение общей жесткости воды
- •1. Предмет аналитической химии.
- •2. Краткая история развития аналитической химии.
- •3. Методы аналитической химии.
- •4. Основные стадии химического анализа.
- •5. Статистическая обработка результатов измерений.
- •6. Отбор проб.
- •7. Потери и загрязнения при отборе пробы. Хранение пробы.
- •8. Подготовка пробы к анализу.
- •9. Аналитическая реакция и её характеристики.
- •10. Дробный и систематический анализ.
- •37. Сущность гравиметрического анализа.
- •38. Типы гравиметрических определений.
- •39. Теория осаждения.
- •40. Операции гравиметрического анализа.
- •41. Расчеты в гравиметрическом анализе.
900
5.4 ОСНОВНЫЕ ПОНЯТИЯ И ПОСТУЛАТЫ ХИМИЧЕСКОЙ КИНЕТИКИ. КИНЕТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ ПРОТЕКАНИЯ ХИМИЧЕСКИХ РЕАКЦИЙ РАЗЛИЧНЫХ ТИПОВ. КАТАЛИЗ
ПЛАН
5.4.1 Предмет химической кинетики.
5.4.2 Основные понятия химической кинетики.
5.4.3 Кинетический закон действия масс – основной постулат химической кинетики.
5.4.4 Кинетические особенности протекания простых реакций.
5.4.5 Методы определения порядка реакции и константы скорости по экспериментальным данным.
5.4.6 Кинетические особенности протекания сложных реакций.
5.4.7 Зависимость скорости реакции от температуры.
5.4.8 Кинетика цепных реакций.
5.4.9 Кинетика фотохимических реакций.
5.4.10 Основы кинетики гетерогенных процессов.
5.4.11 Катализ.
5.4.1 Предмет химической кинетики
Законы химической термодинамики позволяют определить направление протекания равновесный состав и энергетический эффект
химической реакции. Однако эта наука не может ответить на вопросы о том, как осуществляется данная реакция и с какой скоростью. Эти вопросы, а
именно, вопросы о механизме и скорости протекания химической реакции
входят в область компетенции химической кинетики.
Химическая кинетика или кинетика химических реакций (от греч. κίνησις – движение) – радел физической химии, изучающий закономерности протекания химических реакций во времени, зависимости этих закономерностей от внешних условий, а также механизмы химических превращений. В отличие от термодинамики, химическая кинетика изучает протекание химических реакций во времени. Т.е. термодинамика изучает начальное и конечное состояние системы, а химическая кинетика изменение системы при переходе из начального состояния в конечное состояние. Например, реакция
С+О2 → СО2
с точки зрения термодинамики весьма благоприятна, во всяком случае, при температурах ниже 1000° С (приболее высоких температурах происходит уже распад молекул СО2), т.е. углерод и кислород должны (практически со 100%-ным выходом) превратиться в диоксид углерода. Однако опыт показывает, что кусок угля может годами лежать на воздухе, при свободном

901
доступе кислорода, не претерпевая никаких изменений. То же можно сказать и о множестве других известных реакций. Таким образом, знание кинетических закономерностей важно также при хранении и эксплуатации химических продуктов, когда надо замедлить их деструкцию. Это важно, например, при хранении пищевых продуктов, лекарств, топлива, полимеров.
Химическая кинетика решает следующие задачи, перечисленные в порядке сложности их решения:
-Установление экспериментальным путем зависимости между скоростью химической реакции и условиями ее проведения (оптимизировать химический процесс) – прямая задача.
-Установление механизма химической реакции – обратная задача.
-Установление связи между строением химических соединений и их реакционной способностью.
5.4.2 Основные понятия химической кинетики
Скорость химической реакции – число элементарных актов химического взаимодействия, протекающих в единицу времени в единицу объема (гомогенные) или на единице поверхности (гетерогенные). Она может быть средней (формула 5.4.1):
(5.4.1)
или мгновенной при t → 0 (формула 5.4.2)
(5.4.2)
где n1, n2 – число молей вещества в объеме V в моменты времени t1 и t2 , соответственно.
При условии постоянства объема выражения (5.4.1) и (5.4.2) упрощаются (формулы 5.4.3 и 5.4.4):
(5.4.3)
(5.4.4)
и скорость определяется изменением концентрации реагирующего вещества в единицу времени.
Скорость реакции всегда положительна. Однако при протекании реакции во времени концентрации исходных веществ уменьшаются, а продуктов реакции возрастают. В результате соотношение C / t и производная dC / dt могут быть положительными или отрицательными в

902
зависимости от того, изучают скорость реакции по изменению концентрации одного из продуктов реакции (знак "+") или одного из исходных веществ (знак"-").
Скорость реакции как производная от концентрации по времени может быть выражена для любого вещества, участвующего в реакции. Например, для реакции, протекающей по уравнению (5.4.5):
(5.4.5)
где a, b, c и d – стехиометрические коэффициенты, скорость реакции может быть представлена несколькими выражениями (5.4.6):
(5.4.6)
В реакции (5.4.5) исходные вещества расходуются, а продукты реакции образуются в эквивалентных количествах (соответственно стехиометрическим коэффициентам), поэтому при определении скорости реакции нет необходимости следить за изменением концентрации всех взаимодействующих веществ. Достаточно знать изменение концентрации во времени одного из веществ, участвующих в реакции согласно уравнению
(5.4.6).
Скорость реакции зависит от природы реагирующих веществ, их концентрации, присутствия посторонних веществ (например, катализаторов) и их концентрации, среды в которой протекает реакция и условий ее протекания: температуры, давления (для реакций, протекающих в газовой фазе), облучения (фотохимические реакции) и т.д.
Механизм реакции – детальное ее описание с учетом всех промежуточных стадий и промежуточных веществ, природы взаимодействия реагирующих частиц, характера разрыва связей, изменения энергии химической системы на всем пути ее перехода из исходного в конечное состояние. Цель изучения механизма реакции – возможность управлять ходом реакции, ее направлением и эффективностью.
По своему механизму химические реакции делятся на множество групп, среди которых отметим:
А) Последовательные механизмы типа D→S → R→P, где S и R – промежуточные продукты.
Б) Параллельные механизмы: когда одно и то же вещество А может превращаться в различные продукты R и S.
В) Цепные механизмы, когда в ходе реакции возникают особые активные частицы – химические радикалы – которые самовоспроизводятся в элементарных актах.
Понятие элементарного акта возникло при рассмотрении химических превращений на атомно-молекулярном уровне.

903
Каждое единичное превращение исходной или промежуточной частицы (молекулы, иона, свободного радикала, комплекса и т. п.)
называется элементарным актом.
Совокупность однотипных элементарных актов называют
элементарной реакцией или элементарной стадией.
В ходе элементарной реакции преодолевается только один потенциальный барьер (риунок 5.4.1 а) или ни одного (рисунок 5.4.1 б).
Рисунок 5.4.1 – Возможные профили потенциальной энергии для элементарной реакции
Пример реакции типа «а»:
Пример реакции типа «б»:
|
|
|
|
|
|
H + H + Ar |
H |
2 |
+ Ar. |
||
|
|
|
|
|
|
Впоследней реакции атом Ar нужен для того, чтобы обеспечить отвод большого количества энергии, выделяющейся при рекомбинации.
Различие между простой и элементарной реакцией состоит в том, что простая реакция иногда может состоять из нескольких элементарных.
Простыми называются реакции, состоящие только из одной стадии. Сложными называются реакции, состоящие из двух и более стадий. Две важнейшие характеристики элементарных реакций – это их
порядок и молекулярность.
Взависимости от числа молекул, участвующих в элементарной реакции, она может быть (молекулярность реакции):
- Мономолекулярной; - Бимолекулярной; - Тримолекулярной.
Элементарные реакции более высокой молекулярности не наблюдаются ввиду малой статистической вероятности одновременного столкновения четырех частиц. Поэтому реакции с участием более чем трех
частиц всегда не элементарные.

904
Молекулярность реакции, таким образом, является характеристикой ее природы и ее следует отличать от порядка, который равен сумме степеней при концентрациях в уравнении для скорости реакции и является формальнокинетической характеристикой реакции (смотри раздел 5.4.3).
Кинетическое уравнение – это уравнение, описывающее
зависимость скорости химической реакции от концентраций компонентов реакционной смеси.
Изучение кинетики конкретных химических реакций начинается, как правило, с построения экспериментально определяемых зависимостей сi=f(t), которые носят название кинетических кривых. Далее начинается анализ этих данных и изучение механизма протекания реакции. Но это требует длительных и сложных исследований, поэтому после того, как получены кинетические кривые, можно обработать эти данные с получением достаточных для большинства практических целей кинетических уравнений.
На этом этапе кинетических исследований основным законом химической кинетики является закон действующих масс, сформулированный норвежскими учеными Гульдбергом и Вааге.
5.4.3 Кинетический закон действия масс – основной постулат химической кинетики
Основным законом химической кинетики является постулат, выражающий зависимость скорости реакции от концентрации реагирующих веществ: скорость реакции в каждый момент времени пропорциональна произведению концентраций реагирующих веществ, возведенных в некоторую степень (закон действия масс). Так, для реакции (5.4.5) скорость может быть записана (формула 5.4.7):
(5.4.7)
где dC / dt – производная концентрации по времени для веществ А или В (см. уравнение 5.4.6), а CA и CB – концентрации А и В в момент времени t, соответственно. Уравнение, связывающее скорость реакции с концентрациями реагирующих веществ, называется кинетическим уравнением.
Коэффициент пропорциональности k в уравнении (5.4.7) называется константой скорости реакции. Она равняется скорости реакции при условии, если концентрация каждого из реагирующих веществ равна единице, поэтому ее называют также удельной скоростью реакции. Такой физический смысл константы скорости указывает на то, что величина ее должна зависеть от всех факторов, которые влияют на скорость реакции, за исключением концентрации реагирующего вещества. Числовое значение константы зависит также от выбора единиц времени и концентрации. Размерность ее определяется тем, кинетическим уравнением по которому производится ее расчет, т.е. зависит от порядка реакции.

905
Зная константу скорости и порядок реакции по уравнению (5.4.7) можно определить скорость реакции при любых концентрациях реагирующих веществ. Или используя кинетическое уравнение в интегральной форме (вид уравнения будет зависеть от порядка реакции), можно определить степень превращения вещества за определенное время или решить обратную задачу – задаваясь степенью превращения вещества, определить необходимое время процесса.
Показатели степени при концентрациях в кинетическом уравнении (7) α и β называются порядком реакции по веществу А и В, соответственно (или частными порядками). Сумма частных порядков α + β = m называется
полным или суммарным порядком реакции.
Порядок реакции является чисто эмпирической величиной. Только для элементарной реакции, протекающей в один этап, он равен ее молекулярности, т.к. стехиометрическое уравнение правильно отражает истинный механизм такой реакции.
Протекание реакции сложным путем, в несколько стадий, является одной из причин расхождения между порядком реакции и ее молекулярностью. Другой причиной расхождения может быть значительный избыток одного из реагентов в реакционной смеси. Тогда концентрация этого реагента остается практически постоянной в ходе реакции, а порядок реакции будет меньше, чем определяемый по стехиометрическому уравнению.
Частные порядки α или β уравнения (5.4.7) могут быть равны 0, 1, 2 и 3 и тогда говорят о нулевом, первом и втором или третьем порядке по данному веществу. В общем случае порядок реакции m может быть любой величиной (0, отрицательной, положительной; целочисленной, дробной).
Реакции нулевого порядка получаются при независимости скорости от концентрации реагирующего вещества. Это встречается, главным образом, среди гетерогенных реакций, протекающих на поверхности или, если концентрация реагирующего вещества поддерживается постоянной.
Каталитические реакции также могут иметь первый порядок по катализатору и нулевой по веществу.
5.4.4 Кинетические особенности протекания простых реакций
Для реакции нулевого порядка скорость может быть записана уравнением (5.4.8):
(5.4.8)
Разделив переменные, после интегрирования получим:

906
Тогда получим выражение (5.4.9):
(5.4.9)
Или выражение (5.4.10):
(5.4.10)
Из последнего уравнения может быть определена размерность k. Если концентрация С в моль/л, а время в секундах, то константа скорости k в моль
л-1 с-1.
Уравнение (5.4.10) можно записать как
т.е. график в координатах Сt – t будет линейным, а угол наклона будет зависеть от k.
Рисунок 5.4.2 – График зависимости концентрации от времени для реакции нулевого порядка.
Наряду с константой для характеристики химической реакции пользуются величиной периода полураспада (полупревращения) t1/2 ,
равного промежутку времени, в течение которого прореагирует половина исходного количества вещества. Принимая Ct = 0,5 C0 из уравнения (10) получим выражение (5.4.11):
(5.4.11)

907
т.е. для реакций нулевого порядка время полупревращения прямо пропорционально исходной концентрации.
К реакциям первого порядка относятся реакции изомеризации, термического разложения веществ, радиоактивного распада и многие биомолекулярные реакции при условии, что концентрация одного из реагирующих веществ остается постоянной. Для реакции типа А→ С скорость выражается уравнением
Разделив переменные, − dC C = kdt , после интегрирования получим:
При t = 0, C = C0 . Тогда const = − lnC0
и можно записать выражение (5.4.12):
(5.4.12)
Запишем уравнение (5.4.12) в виде:
т.е. график в координатах lnCt – t будет линейным; по углу наклона этого графика можно оценить k.
Рисунок 5.4.3 – График зависимости логарифма концентрации от времени для реакции первого порядка

908
Размерность константы реакции согласно уравнению (5.4.12) время-1 ([t]-1), а время полупревращения при Ct = 0,5 C0 (формула 5.4.13):
(5.4.13)
Для реакции первого порядка t1/2 не зависит от концентрации реагирующего вещества.
Примером реакции второго порядка может служить омыление сложного эфира щелочью. Скорости реакций типа А + В → продукты или
2А → продукты, при условии CA,0 =CB,0 могут быть записаны:
После разделения переменных и интегрирования получается уравнение:
Значение const интегрирования получают при t = 0 и C = C0
Тогда получим выражение (5.4.14):
(5.4.14)
Уравнение (5.4.14) преобразуем:
т.е. график в координатах 1/Ct – t будет линейным; по углу наклона этого графика можно оценить k.
Рисунок 5.4.4 – График зависимости обратной концентрации от времени для реакции второго порядка.

909
Размерность константы скорости будет концентрация-1 время-1 ([C]-1[t]- 1), а период полупревращения (формула 5.4.15):
(5.4.15)
Для реакций второго порядка t1/2 обратно пропорционально начальной концентрации вещества.
Реакции третьего порядка могут быть описаны схемой: А+В+С →
продукты или 2А+В→ продукты, 3А→ продукты и т.д.
При условии СА,0=СВ,0=СС,0 скорость реакции может быть записана:
ω = kC3 или − dC dt = k C3 . После разделения переменных и интегрирования получим:
при t = 0 и C = C0 , const =1/2 C02
и тогда (формула 5.4.16):
(5.4.16)
k = [[C]-2[t]-1], а время полупревращения (формула 5.4.17)
(5.4.17)
Т.е. для реакций третьего порядка t1/2 обратно пропорционально квадрату начальной концентрации.
В случае реакций n-го порядка
А+В+С......→ продукты реакции
при СА,0=СВ,0.......=С скорость реакций равна
После разделения переменных и интегрирования получается (формула
5.4.18):

910
(5.4.18)
и если Сt=С0 / 2 , то время полупревращения (формула 5.4.19)
(5.4.19)
Уравнения (5.4.18) и (5.4.19) не выполняются для реакций первого порядка. Таким образом, чтобы вычислить величину константы скорости химической реакции, необходимо определить порядок реакции.
5.4.5 Методы определения порядка реакции и константы скорости по экспериментальным данным
Для определения порядка реакции необходимо иметь данные об изменении концентрации реагирующих веществ во времени (т.е. иметь кинетическую кривую).
1.Метод «подбора уравнений» или метод «проб и ошибок» основан на подстановке экспериментальных данных по концентрации веществ для каждого момента времени (из кинетической кривой) в кинетические уравнения реакций различных порядков. Определяемый порядок реакции соответствует тому уравнению, для которого в различные моменты времени при заданной температуре константа скорости реакции k будет оставаться постоянной величиной (аналитический метод).
Графический метод основан на том, что определяют такую функцию от концентрации, которая на графике зависимости ее от времени дает прямую линию. В соответствии с кинетическими уравнениями (5.4.10), (5.4.12), (5.4.14), (5.4.16) такими функциями являются: для реакции нулевого порядка
–Сt; реакций первого порядка – lnCt; реакций второго порядка – 1/ Сt .
2.Метод Раковского. В данном методе изучают зависимость периода полупревращения от С0. Для реакций первого порядка (уравнение 5.4.13) t1/2 не зависит от начальной концентрации вещества.
Для реакции n-го порядка уравнение (19) может быть записано
(формула 5.4.20):
(5.4.20)
где
и после логарифмирования получим выражение (5.4.21):

911
(5.4.21)
Зависимость lgt1/2 от lgC0 представляет прямую линию, тангенс угла наклона которой равен (n-1).
3. Дифференциальный метод Вант-Гоффа. Метод основан на использовании уравнения для скорости реакции в дифференциальной форме.
Так графический вариант метода Вант-Гоффа основан на использовании уравнения ω = k Cn, после логарифмирования которого получают (формула 5.4.22):
(5.4.22)
На графике в координатах lgω – lgC полученная зависимость изображается прямой линией с тангенсом угла наклона к оси lgC, соответствующимпорядку реакции (tgϕ = n). Скорость ω определяется тангенсом угла наклона касательной к кривой C = f (t) относительно оси времени как показано на рисунок 5.4.5.
Рисунок 5.4.5 – Определение порядка реакции по методу Вант-Гоффа:
а– определение скорости реакции в различные моменты времени,
б– определение порядка реакции.
Если в реакции участвуют несколько веществ, то пользуются методом изолирования Оствальда. Так для реакции А+В+С→ продукты кинетическое уравнение может быть записано (формула 5.4.23):
(5.4.23)
Сначала проводят реакцию с большим избытком веществ В и С (в 10100 раз больше, чем концентрация А). Тогда уравнение (5.4.23) может быть записано (формула 5.4.24):

912
(5.4.24)
где k ′ = k CB β CC γ. При таких условиях определяют α одним из изложенных выше методов. Во втором опыте берут в избытке А и С и определяют β и т.д.
5.4.6 Кинетические особенности протекания сложных реакций
По своему механизму сложные химические реакции делятся на множество групп, среди которых отметим:
1) Последовательные механизмы типа
А → В → С → Р,
где В и С – промежуточные продукты.
2) Параллельные механизмы:
когда одно и то же вещество А может превращаться в различные продукты В и С.
3) Обратимые реакции
Реакции называются последовательными, если продукт, образующийся в одной из стадий, расходуется в другой. Примером последовательной реакции (5.4.25) может быть процесс, в котором протекает два элементарных акта:
(5.4.25)
где вещество X будет промежуточным соединением. Примерами таких реакций могут служить:
1)радиоактивный распад;
2)анодные процессы Cl- → ClO- → ClO3-
Запишем систему кинетических уравнений для реакции (5.4.25), получим:

913
Эта система кинетических уравнений может быть аналитически решена. Кинетические кривые реагентов, промежуточных и конечных веществ представлены на рисунке 5.4.6.
Рисунок 5.4.6 – Типичный пример экспериментально наблюдаемых кинетических зависимостей для последовательной реакции
Две и более реакции называются параллельными, если в каждой из них участвует одно и то же исходное вещество.
На практике чаще всего приходится иметь дело с двумя типами параллельных реакций.
А) Реакции типа
соответствующие нескольким каналам одного и того же превращения. Учитывая независимость событий превращения по каждому из
каналов, имеем уравнение (5.4.26):
(5.4.26)
и если при  имеем выражения (5.4.27 и
имеем выражения (5.4.27 и
5.4.28):
(5.4.27.)
(5.4.28)

914
Очевидно, что превращение будет в основном идти по каналу с наибольшей константой скорости.
Б) Реакции типа
в которых из одного вещества по параллельным каналам образуется несколько разных конечных продуктов. Здесь есть условие материального баланса А+Х1+Х2+Х3=const
Примем, что при t=0, A0= a, Xi = 0 для всех веществ Xi . Тогда для исходного вещества по-прежнему (как и в случае) имеем выражение (5.4.29):
(5.4.29)
Для продуктов получим
Как видим, доля каждого из веществ в образовавшихся продуктах Х1, Х2….Хi … в любой момент времени составляет
Из анализа экспериментальной зависимости А от t можно найти
из отношений
константы ki порознь.
Обратимые реакции – реакции, протекающие в двух направлениях: прямом и обратном. Поэтому часто обратимые реакции называют двухсторонними. Реакции в большинстве случаев являются обратимыми, т.е. не идут до конца, а в какой-то момент времени устанавливается равновесие между прямой и обратной реакцией. Причем в условиях равновесия скорость прямой и обратной реакции равны, а сама скорость обратимой реакции равна разности скоростей прямой и обратной реакции.

915
Для обратимых реакций закон действующих масс записывается следующим образом:
 .
.
Если начальные концентрации веществ A и B обозначить, соответственно, a и b и ввести степень превращения x ([A] = a - x, [B] = b + x), то кинетическое уравнение приобретает вид:
 .
.
Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия (формула 5.4.30):
Или |
, |
(5.4.30) |
где x определяется условием равенства скоростей прямой и обратной реакций:
,
откуда следует выражение (5.4.31):
. (5.4.31)
При t  ∞ наступает равновесие, которое характеризуется константой:
∞ наступает равновесие, которое характеризуется константой:
Для большинства сложных реакций, включающих несколько элементарных стадий, кинетические уравнения обычно настолько сложны, что их можно точно решить только численным интегрированием. В то же время, разные константы скорости, входящие в эти уравнения, отличаются друг от друга во много раз, что позволяет при решении кинетических уравнений использовать приближенные методы.
Мы рассмотрим два основных метода – метод квазистационарных (иногда просто – стационарных) концентраций и квазиравновесное приближение – на примере кинетической схемы:

916
1. Приближение квазистационарных концентраций применяют в том случае, когда в ходе реакции образуются неустойчивые промежуточные вещества. Если скорость распада этих веществ намного превышает скорость их образования, то концентрация веществ в любой момент времени мала. Раз мала концентрация, то мала и скорость ее изменения, которую приближенно принимают равной 0. Условие квазистационарности позволяет выражать концентрацию промежуточных веществ через концентрации исходных веществ и тем самым упрощать кинетические уравнения.
Для приведенной выше схемы система кинетических уравнений имеет
вид:
Если k2 >> k1, то B – неустойчивое промежуточное вещество, концентрацию которого можно считать квазистационарной:
 ,
,
Откуда
.
Скорость образования продукта равна (формула 5.4.132):
 . (5.4.32)
. (5.4.32)
Таким образом, мы выразили скорость реакции через концентрацию исходного вещества, установили порядок реакции (первый) и выразили эффективную константу скорости через константы скорости отдельных элементарных реакций.
Приближение квазистационарных концентраций обычно применяется к реакциям с участием свободных радикалов, которые представляют собой реакционноспособные неустойчивые частицы.
2. Квазиравновесное приближение применяют в том случае, когда одна из реакций - обратимая, причем равновесие быстро устанавливается и

|
917 |
|
|
медленно разрушается. Для приведенной выше |
схемы это |
означает, |
|
что k2 << k-1. |
Тогда концентрацию промежуточного |
продукта |
B можно |
выразить через константу равновесия: |
|
|
|
|
. |
|
|
Скорость реакции равна (формула 5.4.33): |
|
|
|
|
. |
(5.4.33) |
|
Опять, |
как и в приближении квазистационарных концентраций, мы |
||
получили реакцию первого порядка, однако с несколько отличающейся эффективной константой скорости. Уравнение (5.4.32) сводится к уравнению (5.4.33) при условии, что k2 << k-1.
Из рассмотрения данной схемы следует, что приближение квазистационарных концентраций и квазиравновесное приближение в некотором смысле противоположны друг другу: первое приближение применимо тогда, когда промежуточное вещество распадается быстро, а второе – когда оно распадается медленно.
5.4.7 Зависимость скорости реакции от температуры
Скорость химических реакций с повышением температуры резко возрастает. Эта зависимость для гомогенной реакции приближенно описывается эмпирическим правилом Вант-Гоффа: при нагревании на 100 константа скорости увеличивается в два-четыре раза (формула 5.4.34):
(5.4.34)
где γ – температурный коэффициент, kt+10 и kt константы скорости реакции при температуре t +10 и t, соответственно.
Определив γ, можно приближенно рассчитывать константу скорости в небольшом интервале относительно невысоких температур по уравнению
(5.4.35):
(5.4.35)
Более точная зависимость скорости реакции от температуры (T) описывается уравнением Аррениуса (5.4.36):
(5.4.36)
где k – константа скорости реакции, А – эмпирическая постоянная, называемая предэкспоненциальным множителем и численно равная

918
константе скорости при T → ∞ , E – эмпирическая постоянная, имеющая размерность энергии (энергия активации), T – термодинамическая температура , R – универсальная газовая постоянная.
Энергией активации реакции согласно теории соударений, называется минимальная энергия (в расчете на 1 моль), которой должны обладать реагирующие частицы, чтобы столкновение между ними привело к взаимодействию. Частицы, энергия которых больше или равна E, называются активными. Эта энергия необходима для преодоления энергетического барьера реакции. Столкновение будет эффективным, если суммарная энергия сталкивающихся частиц равна или больше энергии активации E, характерной для данной реакции. Для сложной реакции (протекающей в несколько стадий) параметр E в уравнении Аррениуса не равен энергии активации лимитирующей стадии, а представляет некоторую функцию энергий активации отдельных стадий или вообще эмпирическую величину.
Самый простой способ определения энергии активации E использование уравнения Аррениуса (5.4.36) при температурах T1 и T2, что дает (формула 5.4.37):
(5.4.37)
отсюда – возможность расчета E по константам скоростей при двух температурах. Меньшую ошибку в значении E получают при построении графической зависимости ln k от 1/T, соответствующей уравнению (5.4.36), когда известен ряд констант скоростей при различных температурах.
5.4.8 Кинетика цепных реакций
Цепная реакция – сложная реакция, в которой промежуточные активные частицы, регенерируясь в каждом элементарном акте, вызывают большое число (цепь) превращений исходного вещества.
Механизм этих реакций был открыт Н.Н. Семеновым с сотр. и С. Хиншельвудом с сотр. в 1925-28 гг. Изучая условия воспламенения паров фосфора, Н.Н. Семенов, Ю.Б. Харитон и З.Ф. Вальта установили, что переход от отсутствия реакции к вспышке паров происходит при строго определенном давлении кислорода, которое зависит от диаметра сосуда. В 1928 г. Семенов предложил цепной разветвленный механизм процесса с участием атомов кислорода.
С. Хиншельвуд изучал в 20-х годах окисление водорода кислородом. Для протекания этой реакции также характерны пределы по давлению (нижний и верхний), внутри которых и наблюдается воспламенение смеси. В 1928 г. Хиншельвуд предложил цепную разветвленную схему процесса, где разветвление осуществляют возбужденные молекулы воды и кислорода. Детальное изучение реакции водорода с кислородом в лабораториях Хиншельвуда и Семенова привело к построению и обоснованию механизма

919
этой цепной разветвленной реакции с участием в ней атомов водорода и кислорода и радикалов гидроксила. Важнуюроль в становлении теории разветвленных цепных реакций сыграли исследования В. Н. Кондратьева, который обнаружил гидроксильный радикал в горящем водороде и изучил его поведение и реакционную способность.
Цепная радикальная реакция реализуется, если превращение реагентов происходит через активные промежуточные частицы – атомы и радикалы, а реакции с их участием образуют замкнутый цикл превращений и продолжение цепи осуществляется быстрее, чем обрыв. Цепная реакция является разветвленной, если в ней протекает такая стадия, в которой один радикал или атом генерирует образование нескольких атомов и радикалов. В результате при благоприятных условиях в ходе реакции нарастает концентрация активных центров и, соответственно, увеличивается скорость реакции. Это часто приводит к воспламенению или взрыву.
По данному принципу идут такие реакции как:
1)окисление молекул кислородом;
2)галогенирование многих соединений;
3)реакции термического распада;
4)реакции полимеризации.
Для любой цепной реакции существуют следующие стадии:
1)зарождение цепи – образование свободной радикала;
2)продолжение цепи – сохранение свободной валентности;
3)обрыв цепи – исчезновение свободной валентности. Рассмотрим каждую стадию более подробно.
При зарождении цепи существуют различные пути. К ним можно
отнести:
-мономолекулярный распад
-бимолекулярные реакции
-инициирование светом или радиацией → ̇.
В ходе обрыва цепи также существует несколько путей:
-столкновение радикалов со стенкой ̇
-рекомбинация ̇̇

920
- обрыв на молекулах ингибиторах, которые неспособны вести продолжение цепи.
Звено цепи – совокупность последовательных реакций продолжения цепи, из многократных повторений которых складывается процесс.
5.4.9 Кинетика фотохимических реакций
Химические реакции, протекающие под воздействием электромагнитных излучений (света), называются фотохимическими. Например, при смешении газов водорода и фтора в темноте реакция не проходит, однако при освещении системы она идет со взрывом:
При засвечивании фотопленок проходит реакция восстановления серебра, в результате которой образуется черный осадок высокодисперсного серебра:
Поглощение света необходимо для протекания реакции фотосинтеза, которая будет далее подробно рассмотрена.
Качественно фотохимические реакции подчиняются закону Гроттгуса-Дрейпера: химические превращения вещества может вызывать только тот свет, который этим веществом поглощается.
Явление поглощения света было исследовано в XVIII веке Бугером и Ламбертом, а в XIX веке Бером был сформулирован обобщенный закон поглощения света веществом, согласно которому: количество поглощенного веществом светового излучения зависит от интенсивности и природы падающего света, толщины светопоглощающего слоя, природы и концентрации компонента, взаимодействующего со светом.
В интегральном виде закон Бугера-Ламберта-Бера (БЛБ) имеет вид
(формула 5.4.38):
(5.4.38)
где I0 и I – соответственно интенсивности падающего и прошедшего через раствор света, l – толщина поглощающего слоя, с – концентрация вещества в растворе, ε – молярный коэффициент светопоглощения, зависящий от длины волны света, природы вещества и температуры. Количество поглощенного света ΔI можно найти по разнице интенсивности падающего и прошедшего через раствор излучения (формула 5.4.39):
(5.4.39)
Для удобства измерений светопоглощения вводят параметры: светопропускание (Т) и оптическая плотность среды (D) (формулы 5.4.40– 5.4.42):

921
(5.4.40–5.4.42)
Прямо пропорциональная зависимость оптической плотности от концентрации раствора и толщины поглощающего слоя используется в аналитической химии.
Далее Бунзеном было установлено, что химическое действие света прямо пропорционально произведению интенсивности света на время его действия.
В результате обобщения всех этих закономерностей Вант-Гоффом в 1904 г. был установлен закон: количество химически измененного вещества прямо пропорционально количеству поглощенной веществом световой энергии (формула 5.4.43).
(5.4.43)
где m – количество прореагировавшего вещества, w – мощность светового потока, τ – время (произведение wτ – световая энергия), k – коэффициент, зависящий от природы вещества и температуры.
Закон Вант-Гоффа позволяет понять, например, почему теплолюбивые растения не могут выращиваться в высоких широтах. В приполярных областях, несмотря на большой световой день летом, мощность светового потока настолько мала (лучи преимущественно падают под малым углом к земле), что световой энергии недостаточно для развития растительных организмов. В экваториальных областях световой день составляет около 12 часов, но мощность светового потока очень высока (лучи Солнца падают под углом почти 90°), что и определяет высокую величину световой энергии. Конечно, другими факторами, влияющими на развитие растений, являются их природа и температура (коэффициент k).
Механизм фотохимических реакций определяет закон ШтаркаЭйнштейна: каждому поглощенному кванту излучения hν соответствует одна измененная молекула.
Энергия кванта E = hν, где h – постоянная Планка, ν – частота излучения. Так как длина волны света λ равна частному от деления скорости света с на частоту, то E = hс/λ. Поскольку произведение двух постоянных hс
– величина постоянная (const), то энергия кванта обратно пропорциональна длине волны (формула 5.4.44)
(5.4.44)
Таким образом, чем ниже длина волны света, тем выше энергия кванта. В видимой области спектра максимальной энергией обладают фиолетовые лучи, а минимальной – красные лучи. Например, проявление фотопленки возможно в длинноволновом красном свете, а при освещении коротковолновым излучением видимой области она «засвечивается». Более

922
мощными являются кванты ультрафиолетовой области, а еще более энергоемкими γ-лучи.
При попадании кванта света на молекулу поглощаемый фотон полностью передает им энергию. Иногда этой энергии достаточно для разрыва химической связи, что приводит к протеканию фотохимической реакции с образованием ее продуктов, а иногда нет, тогда молекула переходит в возбужденное состояние. Поэтому в формулировке закона Штарка-Эйнштейна используется слово «измененная», а не «прореагировавшая». Энергия химической связи лежит в интервале 100-500 кДж/моль и поэтому фотохимическую реакцию вызывают только излучения с фотонами, энергия которых не ниже этих величин. Такие кванты называются фотохимическими.
Эффективность фотохимической реакции характеризуется понятием «квантовый выход». Квантовым выходом γ называется отношение числа прореагировавших молекул np к числу поглощенных квантов nn (формула
5.4.45):
(5.4.45)
Квантовый выход различных реакций колеблется в достаточно высоких пределах. Например, в реакции
С6Н14 + Br2 = C6H13Br + HBr
он близок к единице, а в реакции
H2 + Br2 = 2HBr
он колеблется от 0 до 2. Очень высокий квантовый выход имеют цепные реакции. Например, реакция между водородом и хлором, протекающая по цепному механизму, имеет квантовый выход от 10 тысяч до 1 миллиона.
Фотосинтез. Фотосинтез, протекающий в зеленых растениях – единственный первоисточник накопления органического вещества на Земле. В год за счет фотосинтеза образуется около 120 миллардов тонн органического вещества, в том числе более 10 миллиардов тонн за счет сельскохозяйственной деятельности. Попутно выделяется жизненно необходимый для дыхания и других процессов кислород.
Фотосинтез – сложный, многостадийный процесс, в результате которого из низкомолекулярных соединений образуются углеводы. Процесс проходит в результате реакции между диоксидом углерода и водой под действием света в присутствии катализатора хлорофилла (X):

923
В отсутствие хлорофилла эта реакция невозможна, а при взаимодействии CO2 с водой может образоваться только угольная кислота.
Впервые роль хлорофилла в фотосинтезе выявлена русским ученым Тимирязевым. Он показал, что хлорофилл является поглотителем света, передающим поглощенную энергию молекулам исходных веществ.
Механизм фотосинтеза очень сложен и до конца еще не выявлен. Существует ряд схем постадийного фотосинтеза. В биохимии как основные выделяют две стадии – световую и темновую.
Однако внутри каждой из этих стадий существуют подстадии. Далее приводится одна из наиболее простых схем фотосинтеза.
Световая стадия.
1)На этой стадии квант света реагирует с хлорофиллом, переводя его молекулу в возбужденное состояние Х*:
2)Возбужденный хлорофилл обладает повышенным запасом энергии и вследствие этого реагирует с молекулой воды с ее распадом на свободные радикалы (частицы с неспаренными электронами) водорода и гидроксила:
3)Радикал водорода Н• обладает повышенной энергией и реагирует с выделившейся молекулой хлорофилла (восстанавливает его):
Восстановленный хлорофилл в соответствии с теорией катализа является промежуточным соединением.
4) Радикалы гидроксила •ОН, вследствие повышенного запаса энергии, являются неустойчивыми и, взаимодействуя между собой, образуют пероксид водорода:
Пероксид водорода также неустойчив и в гетерогенной системе растения распадается на воду и кислород:
Врезультате этих процессов образуется один из продуктов фотосинтеза – кислород.
Темновая стадия.
1) На первом этапе этой стадии происходит передача водорода от молекулы восстановленного хлорофилла молекуле диоксида углерода с образованием формальдегида:
Врезультате катализатор выходит из реакции в неизменном состоянии
иколичестве, что соответствует основному принципу катализа.

924
2) Образующийся формальдегид полимеризуется по схеме:
в результате чего образуется второй продукт фотосинтеза – углеводы (глюкоза, фруктоза или другие моносахариды).
Далее в результате протекания биохимических процессов в растительном организме моносахариды могут превращаться в дисахариды и полисахариды – крахмал, клетчатку, пектин, инулин и другие высшие углеводы. Не все поглощенные кванты идут на образование возбужденного хлорофилла. Квантовый выход фотосинтеза при освещении растений красным светом в среднем составляет 0,34 О2/квант.
5.4.10 Основы кинетики гетерогенных процессов
Когда реакция совершается между веществами, находящимися в разных фазах гетерогенной системы, основной постулат химической кинетики становится неприменимым. В гетерогенных реакциях роль промежуточных продуктов обычно играют молекулы, связанные химическими силами с поверхностью раздела фаз (химически адсорбированные на поверхности). Во всяком гетерогенном химическом процессе можно выделить следующие стадии:
1.Диффузия реагентов к реакционной зоне, находящейся на поверхности раздела фаз.
2.Активированная адсорбция частиц реагентов на поверхности.
3.Химическое превращение адсорбированных частиц.
4.Десорбция образовавшихся продуктов реакции.
5.Диффузия продуктов реакции из реакционной зоны.
Стадии 1 и 5 называются диффузионными, стадии 2, 3 и 4 – кинетическими. Универсального выражения для скорости гетерогенных химических реакций не существует, поскольку каждая из выделенных стадий может являться лимитирующей. Как правило, при низких температурах скорость гетерогенной реакции определяют кинетические стадии (т.н. кинетическая область гетерогенного процесса; скорость реакции в этом случае сильно зависит от температуры и величины площади поверхности раздела фаз; порядок реакции при этом может быть любым). При высоких температурах скорость процесса будет определяться скоростью диффузии (диффузионная область гетерогенной реакции, характеризующаяся, как правило, первым порядком реакции и слабой зависимостью скорости процесса от температуры и площади поверхности раздела фаз).

925
5.4.11 Катализ
остающееся после реакции в неизменном состоянии и количестве, называется катализатором. Изменение скорости реакции в присутствии катализаторов называется катализом.
Если катализатор увеличивает скорость реакции, то он называется положительным, а если уменьшает – отрицательным (ингибитором). Применение тех или иных катализаторов связано с конкретными задачами. Если необходимо повышение выхода массы продукта, то используют положительные катализаторы, а если необходимо предотвратить продукт от разложения или какого-либо химического превращения, то отрицательные. Отрицательные катализаторы используют при консервировании растениеводческой продукции, (уксусная, лимонная, салициловая кислоты), добавляют как антиокислители к полимерным изделиям для предотвращения их деструкции (например, в резину и другие материалы).
Характерной особенностью катализаторов является их избирательное действие. Например, разные катализаторы вызывают образование различных продуктов реакции пропанола-2:
Высшей степенью избирательности обладают биологические катализаторы – ферменты. Ферменты – это белки с большой молекулярной массой (~500 000 Да). Организм человека содержит около тысячи различных ферментов. Они обладаюткрайне дифференцированным каталитическим действием, абсолютной специфичностью. Абсолютная специфичность – это действие фермента на вещество строго определённого состава. Фермент уреаза действует только на мочевину, пепсин – расщепляет только белки и т. д. Кроме абсолютной специфичности ферменты обладают свойством во много раз увеличивать скорость биохимических процессов. Например, период полураспада мочевины при 25 °С в отсутствие катализатора составляет 109 с (31,7 года), а в присутствии фермента уреазы – 10-4 с, то есть распад идёт практически мгновенно.
Действие катализаторов на скорость химических реакций заключается в осуществлении процессов, энергия активации которых отличается от энергии активации некатализируемых реакций. В присутствии положительных катализаторов энергия активации снижается, а в случае отрицательных – увеличивается.

926
Механизм действия катализаторов объясняет теория промежуточных соединений. Согласно этой теории, катализатор образует с одним из реагентов нестойкое промежуточное соединение, которое затем взаимодействует с другим реагентом, в результате чего образуется продукт, а катализатор выходит из сферы реакции в том же состоянии и количестве. Например, реакция
без катализатора протекает медленно, ей соответствует энергия активации Еа. Введённый в процесс катализатор К взаимодействует с одним из исходных веществ (А) и образует непрочное промежуточное соединение (АК*), формированию которого соответствует энергия активации Еа1 < Еа
Это соединение с большой скоростью реагирует с другим исходным веществом, при этом образуется продукт реакции D, а катализатор выделяется в свободном состоянии:
Скорость реакции 2 более медленная, чем реакции 3 (Еа1 > Еа2), но более быстрая, чем скорость реакции 1, и поэтому общая скорость процесса в присутствии катализатора увеличивается.
Катализ бывает двух видов:
1. Гомогенный – катализатор и реакционная смесь образуют однородную (однофазную) систему.
Примером гомогенного катализа является одна из стадий процесса при контактном способе получения серной кислоты, согласно которой оксид серы (IV) окисляется кислородом до оксида серы (VI):
2SO2 + O2 = 2SO3
Эта реакция протекает очень медленно. Катализатором реакции является оксид азота (II). Согласно теории промежуточных соединений и исходя из химических свойств газов, образующих смесь, сначала протекает реакция окисления катализатора:
2NO + O2 = 2NO2 – промежуточное соединение
Являясь сильным окислителем, оксид азота (IV) легко окисляет оксид серы (IV):
SO2 + 2NO2 = SO3 + NO.
При этом катализатор NO выходит из реакции в неизменном состоянии и количестве.

927
2. Гетерогенный катализ отличается тем, что химическая реакция проходит на границе раздела двух фаз и протекает в большее количество стадий, т.е. является сложным процессом. При этом катализатор, как правило, образует твердую фазу, а реагенты находятся в газообразном состоянии или в растворе.
Рассмотрим пример, когда реакционная смесь представляет собой водный раствор (рисунок 5.4.7). Около поверхности раздела катализатора и реакционной смеси образуется диффузионная пленка, и из массы раствора к поверхности катализатора растворенное вещество доставляется путем диффузии (стадия 1). У поверхности катализатора происходит сближение молекул реагирующих веществ (стадия 2), ориентация их на активных центрах катализатора (стадия 3), адсорбция молекул, сопровождающаясядеформацией связей (стадия 4), химическое превращение адсорбированных молекул (стадия 5), десорбция продукта реакции с поверхности катализатора (стадия 6) и удаление продукта с поверхности путем диффузии (стадия 7). Важнейшими стадиями процесса являются 3 и 4. При адсорбции на активных центрах катализатора (выступах, обладающими нескомпенсированными ва-лентностями) происходит заметное изменение в структурно-энергетическом состоянии молекул, которое повышает их реакци-онную способность вследствие ослабления химических связей.
Рисунок 5.4.7 –Схема гетерогенного катализа. 1-7 – стадии процесса. А, В – реагенты, D – продукт реакции
Если при этом энергия взаимодействия между активными центрами и молекулами более 80 кДж/моль, то имеет место хемосорбция, при которой адсорбированные слои молекул являются промежуточными поверхностными соединениями, которые вследствие неустойчивости обладают повышенной реакционной способностью.
Существует несколько теорий гетерогенного катализа. Одной из них является мультиплетная теория Баландина. В основе этой теории лежит принцип структурного соответствия между расположением атомов на активных центрах катализатора и строением молекул реагирующих веществ. Мультиплеты – это активные участки поверхности кристаллической решетки катализатора, имеющие правильную геометрическую конфигурацию. Индексные группы – это отдельные атомы или группировки атомов в молекулах. Процесс адсорбции молекул на катализаторе проходит так, что их

928
индексные группы связываются с разными атомами мультиплета. При этом происходит деформация связей, образование активированного комплекса и протекание каталитической реакции. Например, в процессе
из двух катализаторов с различным расположением активных центров (рисунок 5.4.8) лучшим является первый (I), как отвечающий принципу структурного соответствия. При гидрировании бензола лучше использовать катализатор II.
Рисунок 5.4.8 – Расположение мультиплетовна разных катализаторах
Каталитические процессы, протекающие в биологических системах, являются гетерогенными, так как ферменты можно рассматривать как отдельную твердую фазу в микрогетерогенных системах – клеточном соке, кровяных тельцах и т. д. Очень сложным гетерогенным каталитическим процессом, механизм которого до конца еще не изучен, является фотосинтез.
929
5.5 ПРЕДМЕТ И ЗАДАЧИ ЭЛЕКТРОХИМИИ. ТЕОРИЯ РАСТВОРОВ ЭЛЕКТРОЛИТОВ. НЕРАВНОВЕСНЫЕ ЯВЛЕНИЯ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ. ЭЛЕКТРОДНЫЕ РАВНОВЕСИЯ
ПЛАН
5.51 Предмет и основные разделы электрохимии.
2.5.2 Развитие представлений о строении растворов электролитов. 5.5.3 Электропроводность растворов электролитов.
5.5.4 Электрохимическое равновесие на границе раздела фаз.
5.5.5 Классификация электродов и электрохимических цепей.
5.5.6 Практическое применение метода измерения ЭДС гальванических элементов.
5.5.1 Предмет и основные разделы электрохимии
В 1791 г. итальянский естествоиспытатель Л.Гальвани описал свои опыты по воздействию внешней среды на поведение живых организмов. Он проводил их с использованием в качестве подопытных лягушек. Лягушки прикреплялись одной лапкой к медному крючку, который в свою очередь подвешивался на стальную проволоку. Когда под влиянием внешних воздействий лягушка другой лапкой касалась стальной проволоки, ее сотрясало как будто от электрического разряда. Л.Гальвани сделал вывод, что это поведение является следствием наличия «животного электричества» в лягушке.
А.Вольта, ознакомившись с этим экспериментом, пришел к иному заключению, а именно, что определяющую роль в реакции лягушки играет присутствие в исследуемых опытах разных металлов: меди и стали, а лягушка только играет роль проводника. Для доказательства своей гипотезы он изготовил «батарею» из пластин меди и цинка, и каждую из пластинок отделил от другой прослойкой из материи, смоченной серной кислотой. На концах такой «батареи» (названой впоследствии «вольтовым столбом») возникала разность потенциалов (напряжение) столь большой величины, что на ее полюсах появлялся искровой разряд. Так был создан первый источник электрического тока.
Создание первого источника электрического тока ознаменовало собой начало исследований в области электричества, а затем и магнитных явлений. Именно с электрохимии началось развитие науки об электричестве и магнетизме, (М. Фарадей. Г. Ампер. Дж. Джоуль), которое завершилось созданием знаменитых уравнений Дж. Максвелла, объединяющих описание электрических и магнитных явлений.
«Из совокупности всех проявлений электричества электролиз больше всего способствует получению реальных представлений о природе электрического тока, так как здесь потоки вещества и потоки зарядов – части одного и того же явления».

930
Окислительно-восстановительные реакции. Рассмотрим уравнения следующих реакций:
FeCl2 + 2NaOH = Fe(OH)2 + 2NaCl
HCl + NaOH = H2O + NaCl
Fe + 2HCl = FeCl2 + H2
Fe + CuSO4 = FeSO4 + Cu
Последние две реакции отличаются от двух других тем, что в них происходит изменение степени окисления компонентов. Такие реакции называются окислительно-восстановительными.
Одним из наиболее фундаментальных законов природы является закон сохранения энергии. Его проявление в окислительно-восстановительных реакциях заключается в том, что в них помимо закона сохранения массы, наблюдающегося в любых химических реакциях, должен соблюдаться закон сохранения заряда. Закон сохранения заряда в окислительновосстановительных реакциях проявляется в изменениях степеней окисления элементов, участвующих в ней.
Любое повышение степени окисления называется окислением, а любое понижение степени окисления – восстановлением.
В окислительно-восстановительных реакциях происходит перенос заряда, а единичным зарядом является электрон, т.е. имеет место перенос электрона. Из закона сохранения заряда следует, что суммарная величина заряда реакции равна нулю.
Fe →Fe2+ + 2 e
Cu2+ + 2e →Cu
Fe + Cu2+→ Fe2+ +Cu
Если поместить в один сосуд, заполненный раствором соли цинка, пластинку металлического цинка, а в другой с раствором соли меди медную и соединить эти два раствора трубкой с раствором поваренной соли, то измерительный прибор, подключенный к пластинам, покажет наличие в системе электрического тока. Такие системы называются гальваническими элементами. В рассматриваемом случае гальванический элемент носит название элемента Даниэля-Якоби, рисунок 5.5.1.
Рисунок 5.5.1 – Элемент Даниэля-Якоби.
931
Наличие тока в системе и его знак свидетельствует о переносе электронов от цинка к меди. После опыта цинковая пластина теряет в массе, а масса медной пластинки увеличивается. Очевидно, что присутствуют следующие реакции:
Zn Zn+2 + 2 e Cu +2 + 2e Cu
Cu 2+ + Zn Cu + Zn 2+
Вывод: В окислительно-восстановительных реакциях происходит перенос электронов.
В элементе Даниэля и вообще в любом гальваническом элементе возможность целенаправленного переноса электронов достигается потому, что поверхности, на которых происходит окисление и восстановление, разделены в пространстве, а, следовательно, пространственно разделены поверхности металла, генерирующие электроны и их поглощающие.
Какие выводы можно сделать из рассмотренного выше опыта?
1.С помощью описанного явления мы получили источник электроэнергии (источник электрического тока).
2.Используя физические принципы, заложенные в данном явлении, можно осаждая металл из раствора модифицировать поверхность, придавать ей другие свойства. Что же касается анода, то вследствие того, что анод растворяется, можно осуществлять удавление металла с поверхности, т.e. осуществлять его обработку (в том числе размерную).
Электрохимия – это наука о взаимном превращении энергии окислительно-восстановительных химических реакций в электрическую энергию, и электрической энергии в химическую окислительновосстановительную реакцию.
Применение электрохимических процессов:
1.Химические источники тока.
а) Батареи (первичные источники тока)
б) Аккумуляторы (вторичные (возобновляемые) источники тока в) Топливные элементы
2.Электролиз а) Электроосаждение
б) Получение водорода и кислорода в) Получение чистых металлов из растворов
г) Электрохимическая размерная обработка д) Получение чистых металлов из расплавов е) Электроанализ
3.Другие приложения
а) Коррозия и методы защиты от нее б) Биоэлектрохимия
в) Электрохимические методы защиты окружающей среды г) Электрохимические датчики информации (хемотроника)

932
Выдающийся вклад в развитие электрохимии и ее приложений внесли М. Фарадей (законы электролиза), Г. Деви (получение металлического калия электролизом), С. Аррениус (теория электролитической диссоциации) и др.
Нобелевскими лауреатами за работы в области электрохимии были: С. Аррениус (Швеция, 1903 г. теория электролитической диссоциации), Я. Гейровский, (Чехословакия,1959 г. полярографический анализ), Р.Маркус (США, 1992 г. теория переноса заряда через границы раздела).
Среди русских и советских ученых выдающийся вклад в развитие электрохимии внесли Б.Якоби (открытие гальваностегии), А.Н.Фрумкин (роль двойного слоя в кинетике электрохимических реакций), В.Г.Левич (физико-химическая гидродинамика). С Молдавией связаны такие имена электрохимиков и физико-химиков как А.Н.Фрумкин (родился в Кишиневе в 1895 г.) Л.В.Писаржевский, Ю.С.Ляликов (электро-анализ), Ю.Н.Петров (электрохимическая обработка металлов). Б.Р.Лазаренко (электроискровая обработка металлов).
Законы Фарадея. 1-й закон Фарадея устанавливает прямую пропорциональность между количеством прошедшего через систему электричества и количеством прореагировавшего вещества (формула 5.5.1):
Δm = kэJt = kэq |
(5.5.1) |
где Δm – количество прореагировавшего вещества; k – коэффициент пропорциональности;
q – количество электричества, равное произведению силы тока I
на время t.
kэ– электрохимический эквивалент.
2-й закон Фарадея устанавливает связь между количеством прореагировавшего вещества при пропускании данного количества электричества и его природой.
По этому закону, при постоянном количестве прошедшего электричества массы прореагировавших веществ относятся между собой, как их химические эквиваленты А (формула 5.5.2):
(5.5.2)
Законы Фарадея – основные законы электролиза, согласно которых, количество вещества, выделившегося при электролизе, прямо пропорционально его химическому эквиваленту и количеству прошедшего электричества.
5.5.2 Развитие представлений о строении растворов электролитов
Слово «электролит» означает разлагаемый электричеством (перевод с греч.). Этот термин принадлежит М.Фарадею, который считал, что
933
разложение на ионы происходит только в результате действия электрического тока. Поэтому возникает важный вопрос: В чем природа проводимости электролитов? Существуют ли носители заряда в растворе или они возникают под действием электрического тока?
Первой теорией, объясняющей возникновение ионов в растворе, была теория литовского ученого Т.Гроттгуса (1805г). Он предложил так называемый «эстафетный механизм» возникновения зарядов. Благодаря реакции на границе и удалению положительно заряженного иона, на катоде возникает избыток отрицательного заряда, благодаря которому происходит разделение зарядов у близлежащих молекул и т.д. по эстафете. Но это означает, что разделение зарядов происходит только под действием тока, а в растворе заряды отсутствуют.
Вторая гипотеза принадлежит М.Фарадею: молекулы растягиваются под действием электрического поля и так происходит их диссоциация, разложение.
Однако в дальнейшем оказалось, что это неверно: частично или полностью разложение происходит и без электрического тока, т.е. при растворении. Как это доказать?
При изучении растворов электролитов в середине XIX века был обнаружен ряд отклонений от законов разбавленных растворов:
1. Изменение осмотического давления Росмподчиняется следующему уравнению (5.3.4).
Росм = с RT .
где C – концентрация раствора; R – универсальная газовая постоянная; Т – абсолютная температура.
Измерения показывали, что, например, осмотическое давление раствора сахара в воде описывалось этим соотношением. Однако применение этого уравнения, к водным растворам солей, например, к раствору NaCl, предполагало значительно более низкое значение Росм, чем получалось в эксперименте. Известный голландский ученный Я.Вант - Гофф предложил вводить поправочный коэффициент, названный изотоническим. Тогда для этих растворов можно записать соотношение (i > 1):
Росм = iCRT
Получалось, что в таких растворах как будто бы большее число частиц. 2. Изменение давления пара растворителя над раствором
неэлектролитов можно рассчитать следующим образом:
где р0 – это давление пара над чистым растворителем; М0-
молекулярная масса растворителя; С – моляльная концентрация раствора.
934
Опять же для растворов электролитов совпадение экспериментальных данных и расчетных возможно было только в том случае, если вводился изотонический коэффициент i >1.
3. Изменение температур кипения и замерзания. Криоскопические и эбулиоскопические измерения (это измерения понижения температуры замерзания и повышения температуры кипения растворов по сравнению с чистыми растворителями), показали, что в растворах электролитов экспериментально измеренное понижение температуры замерзания и повышение температуры кипения оказались завышенными по сравнению с расчетными.
Подобные отклонения для растворов электролитов смогла объяснить теория шведского ученного С. Аррениуса, разработанная только в 1887г. Она позволила количественно показать природу процессов, протекающих в растворах электролитов. В основном эта теория сохранила свое значение до настоящего времени.
Основные положения теории электролитической диссоциации С.Аррениуса:
1. При растворении молекулы неорганических и некоторых органических соединений диссоциируют на ионы.
HCl H+ + Cl- NaOH Na+ + OH- K2SO4 2K+ + SO4-2 CH3COOH H+ + CH3COO -
2. Диссоциация молекул на ионы не является полной, вводилась степень диссоциации  .
.
0 < ά < 1.
3. К процессу электролитической диссоциации как к любой химической реакции применим закон действующих масс.
Теория электролитической диссоциации нашла хорошее экспериментальное подтверждение, и за ее разработку в 1903г. С. Аррениус был удостоен Нобелевской премии. Между тем, у теории С. Аррениуса были свои недостатки:
1.Неясен механизм диссоциации молекул на ионы;
2.Непонятно отсутствие взаимодействий между заряженными частицами.
Ион-дипольное взаимодействие. Механизмы образования растворов. Наиболее распространенным в природе растворителем является вода. Она обладает высокой диэлектрической проницаемостью, ε = 83.
Диэлектрическая проницаемость – это отношение напряженности электрического поля в вакууме к напряженности поля в однородной изотропной среде при неизменных зарядах, создающих поле. Она показывает, во сколько раз уменьшается сила взаимодействия электрических

935
зарядов при переносе их из вакуума в однородную изотропную среду, если расстояние между зарядами остается неизменным.
Например для эфира ε = 4,3, что существенно ниже, чем в случае воды, т.е. при переносе заряда из вакуума в среду (воду), сила взаимодействия уменьшается в 83 раза, а из вакуума в эфир лишь – в 4,3 раза.
Именно высокая диэлектрическая проницаемость воды является причиной разложения на ионы. При диссоциации происходит химическая реакция взаимодействия иона с молекулой растворителя (воды). Этот процесс называется сольватацией (гидратацией). Если при растворении в воде или другом растворителе энергия гидратации (сольватации) окажется равной или близкой к энергии связей кристаллической решетки, то в этом случае произойдет разрушение кристаллической решетки вещества и начнется процесс растворения и образования гидратированных (сольватированных) ионов.
Схематически это можно выразить следующим образом:
Рисунок 5.5.2 – Гидратация иона меди
С другой стороны, например, в случае с хлористым водородом происходит его взаимодействие с молекулой воды с образованием соляной кислоты идальнейшей диссоциацией на ионы:
HCl + H2O H3O+ + Cl-
Таким образом, возможны два механизма образования растворов с одновременной диссоциацией на ионы:
1.Если ионы существуют в кристаллической решетке, тогда при растворении в воде (растворителе) гидратная (сольватная) оболочка, стабилизирует существование ионов в растворе (рисунок 5.5.2);
2.Если в веществе, находящемся в газообразном, жидком или твердом состоянии ионы отсутствуют, гидратация обеспечивает их диссоциацию и последующую стабилизацию ионов.
Подобный механизм образования ионов позволяет утверждать, что они образуются не под действием электрического тока, а уже при растворении.

936
Рассмотренный механизм объясняет их устойчивость в растворах электролитов.
Теория С.Аррениуса вместе с теорией гидратации (сольватации), разработанной Д.И. Менделеевым, достаточно хорошо описывала поведение растворов электролитов, но только для разбавленных растворов. Как следует из всего вышеизложенного, она основана на ион-дипольном взаимодействии. Именно ион-дипольное взаимодействие объясняет механизм образования растворов и их устойчивость. Учет ион-дипольного взаимодействия позволил существенно развить теорию С.Аррениуса, однако для концентрированных растворов электролитов это оказалось недостаточным.
Для описания их поведения было введено понятие об активности ионов.
Активность – это кажущаяся (эффективная) концентрация ионов, которая меньше их концентрации, определенной в растворе (формула 5.5.3):
ai = fi Ci, |
(5.5.3) |
где Ci – концентрация иона, ai – его активность; fi – коэффициент активности (безразмерная величина) fi < 1.
Активность зависит от общей ионной силы раствора (формула 5.5.4):
(5.5.4)
где Ci – концентрация иона, а Zi – его заряд.
При постоянной ионной силе раствора коэффициенты активности равны. Был введен средний коэффициент активности (формула 5.5.5):
(5.5.5)
 – число катионов и анионов, образующихся при диссоциации электролита.
– число катионов и анионов, образующихся при диссоциации электролита.
Введение коэффициента активности связано с необходимостью создания теории электролитов для концентрированных растворов.
Теория Дюбая–Гюккеля и ион-ионное взаимодействие в растворах электролитов. В концентрированных растворах электролитов необходимо учитывать взаимодействие ионов друг с другом. Именно это приводит к тому, что как бы снижается их концентрация. П.Дебаю и независимо от него Х.Гюккелю в 1923г. удалось на основе учета ион - ионного взаимодействия рассчитать средний коэффициент активности (формула 5.5.6):
(5.5.6)
где (формула 5.5.7):

937
(5.5.7)
Уравнение (5.5.6) верно для 1-1 валентного электролита. Для более сложных случаев была получена эмпирическая формула Я.Бренстеда
(формула 5.5.8):
(5.5.8)
Теория Дебая–Гюккеля, таким образом, описывает ион–ионное взаимодействие в сильных электролитах и часто носит название теории сильных электролитов. Как видно из соотношений (5.5.6), (5.5.8) теория Дебая–Гюккеля позволила рассчитать для некоторых частных случаев коэффициент активности, который объяснял ион–ионное взаимодействие, снижающее эффективную концентрацию частиц в растворах, учитывая и диэлектрическую проницаемость растворителя (ε) и общую ионную силу раствора (I).
5.5.3 Электропроводность растворов электролитов
Электропроводность отражает физический перенос заряда между электродами и количественно определяет способность объекта проводить электрический ток. Электрический ток есть упорядоченное перемещение заряжённых частиц. Электропроводность растворов электролитов обусловлена перемещением ионов в электрическом поле. Для оценки этой способности в физике используют понятие удельной электропроводности.
К понятию удельной электропроводности можно подойти на основе закона Ома, установленного автором экспериментально в 1826 году и названного в его честь. По закону Ома сила электрического тока (I, Ампер,
А) определяется как отношение разности потенциалов напряжения тока
(Е) на концах проводника (Е = Е2 – Е1, Вольт, В = Вт/А, Вт = Ват → мощность электриче-ского тока силой в 1 А при напряжении в 1 В) к сопротивлению среды R (сопротивление току проводника): I = E/R. Общее сопротивление проводника R (Ом = В/А) пропорционально удельному электрическому сопротивлению (ρ), длине проводника (l, м) и обратно пропорционально площади его поперечного сечения (S, м2) (формула 5.5.9):
(5.5.9)
Из выражения (5.5.9) следует, что размерность удельного электрического сопротивления (ρ) выражается в Ом·м.
Удельное сопротивление (ρ) в системе СИ определяется как сопротивление проводника, между двумя плоскими электродами (║) площадью 1 м2 и длиной 1 м каждый.

938
В термодинамике растворов электролитов величина, обратная удельному электрическому сопротивлению (ρ) получила название удельной электропроводности (κ – «каппа» – шарообразная форма, связанная с объёмом) (формула 5.5.10):
(5.5.10)
Величину удельной электропроводности используют в качестве количественной меры раствора электролита, способной проводить электрический ток. Размерность величины κ в системе СИ:
κ = 1/Ом·м = Ом–1·м–1 = См·м–1,
где См – Сименс (См = Ом–1), единица электрической проводимости, названная в честь немецкого электротехника.
Величина удельной проводимости зависит от природы проводника. Проводимость электролитов в десятки и сотни раз меньше, чем
металлов. Применение удельной электропроводности в химии исключает сопоставление проводимости растворов разных электролитов, так как вещества реагируют и взаимодействуют в эквивалентных количествах (закон эквивалентов).
Поэтому в химии в качестве меры проводимости долгое время использовали эквивалентную электропроводность (λ). Величина удельной электропроводности связана с величиной эквивалентной электропроводности (λ) соотношением κ/с = λ, где с – эквивалентная концентрация раствора электролита.
В системе СИ количество вещества измеряется в молях. В термодинамике растворов значения функций состояния (ΔН, ΔU, ΔS, ΔG, А) отнесены к 1 молю – Дж/моль, кал/моль. И в электропроводности давно
уже используется понятие молярной проводимости (рисунок 5.5.3).
Рисунок 5.5.3 – Типы электропроводности и единицы её измерения
Представленные на схеме единицы проводимости тока можно проиллюстрировать рисунком 5.5.4. Можно взять 3 одинаковые ячейки с основанием 1 м·1м (s=1 м2) и на боковые их стенки тонким слоем напылить металл так, чтобы ячейки могли выполнять роль плоских электродов.

939
Рисунок 5.5.4 – Ячейки, иллюстрирующие типы электропроводности
Впервую ячейку для иллюстрации удельной электропроводности (κ) нальем раствор электролита высотой в 1 м. Тогда величина κ численно равна проводимости слоя электролита в 1 м, находящегося между двумя противоположными гранями куба единичной площади.
Во вторую ячейку – для иллюстрации эквивалентной элек-
тропроводности ( – «лямбда») нальем раствор электролита такой высотой, чтобы в нём содержался 1 кг–экв. растворённого вещества.
– «лямбда») нальем раствор электролита такой высотой, чтобы в нём содержался 1 кг–экв. растворённого вещества.
Втретью ячейку, для иллюстрации молярной электропроводности (μ), нальем раствор электролита такой высоты, чтобы в нём содержалось 1 кмоль растворённого вещества.
Вконце прошлого века А.Г. Стромберг при оценке электропроводности в растворах предложил перейти от нормальной концентрации к молярной (г-экв/л → моль/л). Для растворов с одновалентными ионоконцентрациями их составы в единицах измерения равны. Например, для раствора КCl эквивалент (Э) оценивается отношением молекулярной массы, делённой на валентность ионов (Э = М/1), то есть химический эквивалент численно равен массе одного моля КCl. Для растворов двухосновных электролитов эквивалентную проводимость (λэкв) можно определить, как половинную величину молярной (μm) проводимости
(½Н2SO4, ½MgSO4 → ½μm= λэкв) – рисунок 5.5.5.
Рисунок 5.5.5 – Зависимости удельной электропроводности от концентрации электролита

940
В электрохимии применяют величину обратную концентрации, (1/с = V), которая называется разведение (разбавление) раствора растворителем. Между κ, λ и V существует взаимосвязь (формула 5.5.11):
λ = κ·V = κ/см или κ = λ·см , |
(5.5.11) |
где V – объем растворителя (м3), в котором содержится 1 моль электролита; см – концентрация электролита, выражена в моль/м3; λ – молярная электропроводность, [λ] = См·м2/моль.
В лабораторных условиях с объёмами в 1 м3 не работают, а используют несистемные единицы размерности:
κ =1/Ом·cм = Cм/см. λ = м2/Ом·моль = См·см2/моль; см = моль/л = моль/дм3 = моль/1000 см3.
Для размерности концентрации раствора, выраженной в моль/л или моль/дм3, соотношение (5.5.9 → λ= κ/см) нужно записывать в виде λ= (κ·1000)/см.
Электрическая проводимость электролитов связана со скоростью движения ионов в растворе (ui [м/с]), которая пропорциональна напряжённости приложенного электрического поля (Е) (формула 5.5.12):
(5.5.12)
где ui*– коэффициент пропорциональности, называемый абсолютной скоростью движения иона.
Чтобы исключить влияние напряжённости электрического поля на скорость, принято сравнивать скорость ионов при градиенте напряжённости электрического поля (Е) 1 В/м. Под абсолютной скоростью (ui*) понимают движение ионов при единичном градиенте потенциала в 1 В/м и температуре 25 оС (таблица 5.5.1). Единицы их измерения получают из формулы (5.5.10) – м2/В·с.
Таблица 5.5.1 – Абсолютные скорости движения ионов (ui*, м2/В·с) в водных растворах при 25 °С

941
Абсолютные скорости движения ионов очень малы, поэтому для определения подвижности ионов пользуются числом Фарадея F (96484,5 Кл/моль или Кл/г-экв, Кл=А·с), F которое равно электрическому заряду, переносимому ионами, а их суммарная масса – химическому эквиваленту (численно).
Если выделившееся вещество одновалентное, его химический эквивалент численно равен массе одного моля, а число ионов, перенесших эту массу – числу Авогадро (NA = 6,02·1023).
Число F – фундаментальная физическая константа, равная произведению NA на элементарный электрический заряд е – заряд электрона (он неделим и е=1,6021766208(98)·10−19 Кл). Если же на электроде выделилось двухвалентное вещество, то 96484,5 кулонов переносится числом ионов, вдвое меньшим, чем число Авогадро и т.д. Значения абсолютных скоростей движения ионов определяются с помощью чисел переноса и подвижностей ионов (см. ниже).
Произведение величин ui*·F в правой части выражения (5.5.10)
определяет на физическом уровне количество электричества, переносимое ионом, и это произведение называют абсолютной подвижностью иона.
Важным параметром электролита в растворе является степень диссоциации (α). Если она в растворе бинарного электролита равна α, то концентрациями катионов и анионов будет произведение α·с. Это произведение определяет количество ионов, переносящих электричество, то есть носителей тока в системе.
С позиций изложенного величину удельной электропроводности можно определить как произведение носителей тока (α·с) на подвижность ионов. Тогда для удельной электропроводности (κ) получим выражение
(5.5.13):
(5.5.13)
Размерность величин, входящих в выражение (5.5.13) такова:
В формуле (5.5.11) представлены абсолютные скорости движения ионов. Однако, на практике определить их cовершенно невозможно, поскольку вокруг иона всегда формируется гидратная (сольватная) оболочка. Выражение (5.5.11) применительно к предельно или бесконечно разбавленным (БР) растворам сильных электролитов предполагает следующие допущения:
–степень диссоциации в предельном случае может быть равной единице, ά ≈ 1;
–в БР растворах с → 0;

942
–в БР растворах электролитов ионов мало, и ионы одного знака не мешают движению ионов противоположного знака, то есть каждый ион движется независимо друг от друга с максимальной предельной скоростью;
–значения абсолютных скоростей движения ионов следует определять
вформе равенства скоростей при бесконечном разведении:
 – скорости движения ионов для БР растворов.
– скорости движения ионов для БР растворов.
Тогда формула (5.5.13), с учетом принятых допущений, запишется в выражение (2.4.14):
(5.5.14)
Поделим (5.5.14) на параметр с (с≠0, с→0) и так как κ/см=λ, а для БР растворов λ → λ∞, то получим выражение (5.5.15):
(5.5.15)
где λ∞ – предельная величина молярной (эквивалентной) электропроводности гипотетического бесконечно разбавленного раствора, в котором проходит полная диссоциация электролита (ά ≈ 1).
Произведение F·ui∞ в выражении (5.5.15) называется предельной молярной электрической проводимостью иона или подвижностью иона
при бесконечном разведении. Величины λi∞, отнесенные к отдельным видам ионов, называют также подвижностями бесконечно разбавленных растворов
(формула 5.5.16):
(5.5.16)
Электролитическая подвижность является важным параметром иона, отражающим его участие в электропроводности раствора. Высказывание «Молярные подвижности ионов пропорциональны абсолютным скоростям движения ионов при предельном разведении раствора» на физическом уровне означает: чем выше молярная электропроводность, тем быстрее движется ион в растворе. Для данного вида иона эта величина зависит только от природы растворителя и температуры. Для большинства ионов величина подвижности примерно одинакова, кроме ионов Н3О- и ОН- которые проявляют высокие значения подвижности. Это объясняется эстафетным механизмом передачи заряда этими ионами в растворе.
В 1879 году Ф. Кольрауш показал, что в молярную электропроводность БР-растворов электролитов (λ∞) каждый из ионов вносит свой независимый

943
вклад, и величина λ∞ является суммой молярных электропроводностей катиона (λ+∞) и аниона (λ-∞), то есть их подвижностей.
Величину λ∞ можно представить в виде суммы подвижностей составляющих её ионов (формула 5.5.17):
(5.5.17)
Соотношение (5.5.16), сформулированное Кольраушем, отражает закон о независимой миграции (движении) ионов в растворе. Закон Кольрауша дает возможность по известному значению λ∞ для некоторых электролитов найти λ∞ для данного электролита, если он состоит из тех же ионов. Величина молярной электрической проводимости, определённая по подвижностям ионов, является константой при Т = const. Их значения приведены в справочниках. Соотношение (5.5.17) справедливо и для предельного случая слабых электролитов, если считать, что при БР растворе водой степень диссоциации увеличивается так как увеличивается число молекул растворителя (H2O) на одну молекулу растворённого вещества.
При сильном разбавлении растворов слабых электролитов α (рисунок 5.5.6) возрастает (при с → 0 α → 1) и увеличивается число ионов в растворе.
Рисунок 5.5.6 – Зависимость степени диссоциации α от концентрации слабого электролита в растворе
По принципу Ле Шателье равновесие электролитической диссоциации в этом случае должно сместиться в сторону образования продуктов, то есть гидратированных ионов. При увеличении температуры для раствора слабого электролита степень электролитической диссоциации растёт за счёт активации связей в молекулах, подвижность их возрастает, и они легче ионизируются.
Обобщённое для электролитов правило Кольрауша звучит так: «Молярная электрическая проводимость сильного электролита любой концентрации ( ) и слабого электролита при бесконечном
) и слабого электролита при бесконечном

944
разведении ( ) представляет собой сумму молярных ионных подвижностей».
) представляет собой сумму молярных ионных подвижностей».
На рисунке 5.5.7 приведены качественные зависимости молярной электропроводности от концентрации растворов электролитов. В случае разбавленных растворов связь между концентрацией и молярной электропроводностью совершенно определенная: чем меньше концентрация раствора, тем выше его электропроводность.
Рисунок 5.5.7 – Зависимости молярной электропроводности от концентрации растворов электролитов
Молярная электропроводность и сильных, и слабых электролитов увеличивается, и притом весьма быстро, с увеличением разбавления (V = 1/с), достигая некоторого предельного значения λ∞, называемого молярной электропроводностью при бесконечном разведении (рисунок 5.5.7).
У сильных электролитов при бесконечном разбавлении (БР) уменьшается межионное взаимодействие, подвижность ионов достигает предельных значений, поэтому молярная электрическая проводимость перестает зависеть от концентрации и становится величиной постоянной. Практически это наблюдается уже при концентрациях 10–5–10–4 моль/л, что позволяет экспериментально определять величину предельного разведения (V) для сильных электролитов (рисунок 5.5.8). Для растворов слабых электролитов полная диссоциация даже при очень большом разбавлении практически не достигается, следовательно, экспериментально значения предельного разведения (V) для слабого электролита не могут быть измерены (рисунок 5.5.8). Значения этих величин находят расчётами по соотношению Кольрауша (5.5.16). Представленные на рисунках 5.5.7 и 5.5.8 зависимости имеют нелинейный вид, поэтому экстраполяция их в область бесконечного

945
разведения может привести к погрешностям оценки величины λ∞ для сильных электролитов.
Рисунок 5.5.8 – Зависимости молярной проводимости от разведения
Для увеличения достоверности оценочных величин исследуемые зависимости λ= f(см) (рисунок 5.5.7), линеаризуют, и для бесконечно разбавленных растворов сильных электролитов используют закон Кольрауша в форме корня квадратного от концентрации (λ = f(√с) (формула 5.5.18):
(5.5.18)
Где, а – постоянная, зависящая от природы растворителя, температуры и валентного типа электролита. Значение предельной молярной электропроводности (λi∞) сильных электролитов можно найти экстраполяцией опытных данных до значения концентрации с → 0. Коэффициент пропорциональности – а – определяют по тангенсу угла наклона прямой к оси абсцисс (рисунок 5.5.9). Необходимо подчеркнуть, что хотя предельную электропроводность понимают как проводимость при концентрации электролита, близкой к нулю, она не идентична молярной электропроводности растворителя. Из анализа приведённых зависимостей следует, что лучше всего раствор проводит ток, когда в нём нет электролита. Несмотря на парадоксальность этого вывода, удивляться ему не приходится: чем слабее межионное взаимодействие в растворе, тем свободнее движутся ионы и тем выше электропроводность.

946
Риcунок 5.5.9 – Зависимости молярной электропроводности от концентрации
Поэтому λi∞ – совершенно определенная величина. Она показывает, какой была бы электропроводность раствора, если бы межионное взаимодействие в нем отсутствовало.
Электропроводность растворов электролитов зависит от природы электролита и растворителя. Природа растворителя влияет на степень диссоциации электролита. Диссоциация электролита проходит, как правило, в полярных растворителях и зависит от диэлектрической проницаемости последних (ԑ). Чем она выше, тем полнее диссоциация электролита и больше электропроводность раствора. Довольно большая диэлектрическая проницаемость у воды: при 25 оС  = 78,3. Диэлектрическая проницаемость этанола ниже – 24,3, этиленгликоля – 37,0. Лишь небольшое число органических растворителей имеет ԑ выше, чем у воды. Например, для формамида ԑ = 109,0. Растворы электролитов в таких растворителях имеют очень высокую электрическую проводимость.
= 78,3. Диэлектрическая проницаемость этанола ниже – 24,3, этиленгликоля – 37,0. Лишь небольшое число органических растворителей имеет ԑ выше, чем у воды. Например, для формамида ԑ = 109,0. Растворы электролитов в таких растворителях имеют очень высокую электрическую проводимость.
С другой стороны, чем выше полярность растворителя, тем легче он формирует вокруг иона сольватную оболочку, а значит размеры сольватированного иона больше и, следовательно, меньше его подвижность. В неполярных растворителях типа ССl4 (ԑ = 2,238 при 20 оС, у бензина ԑ = 2,3, у гептана ԑ = 1,9) диссоциация практически отсутствует, и электропроводность таких растворов низка. Можно отметить и другие факторы, влияющие на подвижность ионов в водных растворах при наличии электрического поля (рисунок 5.5.10).
Рисунок 5.5.10 – Факторы, влияющие на электропроводность раствора электролита

947
Величину удельной электропроводности можно представить в виде двух сомножителей – носителей тока (α·с) и подвижности ионов {(u+*)+u-*
F} (формула 5.5.19):
(5.5.19)
Используя выражение (5.5.19) можно исследовать влияние различных факторов на величину электрической проводимости для разных по природе растворов электролитов.
Повышение температуры для растворов сильных электролитов на уровне первого множителя в уравнении (5.5.19) не влияет на параметры с и α. При увеличении температуры у растворов слабых электролитов растёт их степень диссоциации, так как активируются связи в молекулах электролита. Связи становятся более подвижными, они легче ионизируются, и как следствие, растёт концентрация ионов в растворе. Экспериментально установлено, что уже через 1,3·10–16 секунды с момента наложения электрического поля на раствор электролитов ионы будут двигаться со скоростью, близкой к предельной.
На уровне второго множителя выражения (5.5.19) с повышением температуры возрастает скорость движения ионов как для сильных, так и слабых электролитов. Температурная зависимость удельной электропроводности бесконечно разбавленных растворов описывается эмпирическим уравнением (5.5.20):
(5.5.20)
где α и β – температурные коэффициенты электрической проводимости.
Коэффициент α зависят от природы электролита: для сильных кислот α = 0,0164, для сильных оснований α = 0,0190, для солей α = 0,0220.
Наибольший температурный коэффициент отмечен для ионов с относительно малой подвижностью, и наоборот.
Зависимость молярной электропроводности от температуры оценивается по уравнению линейного вида (формула 5.5.21):
(5.5.21)

948
где α – температурный коэффициент электрической проводимости. Температурный коэффициент при средних температурах в водных
растворах для большинства ионов изменяется в пределах 0,02÷0,025, поэтому увеличение удельной и молярной электропроводности раствора при повышении температуры на 1 °C составляет примерно 2–2,5 %. Следовательно, для точного измерения электропроводности необходимо проводить эксперимент в термостатированной системе. При повышении температуры уменьшаются вязкость растворителя, снижается толщина гидратных оболочек ионов и межионное взаимодействие вследствие повышения кинетической энергии ионов с оболочками. Все это приводит к увеличению подвижности ионов.
Можно привести некоторые примеры влияния температуры на скорость движения ионов. Например, в водном растворе NaCl при 0 и 100 оС ионы натрия движутся со скоростями 2,56·10–4 и 13,68·10–4 см/с. Вязкость раствора при этих температурах, соответственно, 0,0178 и 0,00283 сПз. Сравнивая эти два параметра, можно отметить, что с возрастанием температуры раствора электролита скорость движения иона повышается в 5,4 раза, а вязкость снижается в 5 раз. Следовательно, скорость движения ионов в растворах с повышением температуры возрастает, в основном, за счёт снижения вязкости раствора.
Таким образом, при увеличении температуры повышается степень диссоциации слабого электролита, уменьшается вязкость раствора и степень гидратации ионов. Это повышает подвижность ионов и электропроводность раствора.
Вязкость растворителя (ηо) отражается в сопротивлении раствора движению ионов. Чем выше вязкость раствора, тем меньше подвижность ионов и, следовательно, меньше величина электропроводности.
Простейшей моделью движения ионов в жидкости является модель заряженных твёрдых сфер (макроскопического шарика), движущихся в вязком растворителе под влиянием силы, обусловленной градиентом потенциала напряжённости электрического поля (E/l). Сила сопротивления
(η) движению иона в растворе определяется уравнением Стокса. Согласно закону Стокса, предельная скорость движения иона в растворе (ui∞) с зарядом (zi) и эффективным радиусом иона (ri) в чистом растворителе с вязкостью (ηо) представлена формулой (5.5.22):
(5.5.22)
где zi – число зарядов иона; e – заряд электрона; E/l – напряжённость электрического поля.
При вычислении подвижностей для БР растворов напряженность поля (Е/l – движущая сила) принимается равной единице и от скорости (ui∞) можно

949
перейти к подвижности (λi∞), умножиобе части уравнения на число Фарадея → λi∞ = ui ·F (формула 5.5.23):
(5.5.23)
В рамках применимости этого уравнения выполняется правило Вальдена–Писаржевского, в соответствии с которым для одного и того же иона или электролита в любых растворителях произведение предельного значения молярной электропроводности (λi∞ или λ∞) на вязкость чистого растворителя (ηо) является постоянной величиной, которая не зависит от природы растворителя, но является функцией температуры (формула 5.5.24):
(5.5.24)
где λ∞ и λi∞ – мольные электропроводности растворённого электролита и иона, экстраполированные до нулевой концентрации; ηо – вязкость чистого растворителя.
|
Правило Вальдена–Писаржевского приближенно и выполняется лишь |
||||
для |
растворителей |
с |
близкими |
величинами |
диэлектрических |
проницаемостей. Согласно гидродинамической модели это правило сравнительно хорошо выполняется для узкого интервала температур, если радиус иона в растворе постоянен, только для слабо сольватированных ионов, когда ионы имеют большие размеры в кристаллической фазе или для крупных органических ионов.
Концентрация раствора. Повышение концентрации растворённого электролита неоднозначно влияет на электропроводность раствора. Из анализа зависимостей приведённых на рисунках (5.5.5) и (5.5.11) видно, что с увеличением концентрации удельная электропроводность растворов сначала возрастает, достигая некоторого максимального значения, затем начинает уменьшаться.
Эта зависимость очень четко выражена для сильных электролитов и значительно хуже для слабых. Наличие максимума на кривых объясняется тем, что в БР растворах сильных электролитов скорость движения ионов мало зависит от концентрации.
Поэтому кривая сначала растёт почти прямо пропорционально числу ионов в растворе (числу носителей тока) и, как следствие за счёт множителя I уравнения (5.5.19) увеличивается вклад в электропроводность. С увеличением концентрации (выше 5 моль/л) в растворах сильных электролитов усиливается электростатическое взаимодействие ионов, что уменьшает скорость их движения, снижается их подвижность и,

950
следовательно, за счёт II множителя уравнения (5.5.19) электропроводность понижается, рисунок 5.5.11.
Рисунок 5.5.11 – Зависимости удельной электропроводности от концентрации лектролитов
Врастворах слабых электролитов плотность ионной атмосферы мала
искорость движения иона мало зависит от концентрации электролита, поэтому вид зависимости достаточно пологий, рисунок 5.5.11 (зависимость для СН3СООН), но максимум присутствует, хотя и не ярко выраженный. Для БР растворов слабых электролитов наличие максимума на кривой обусловлено тем, что с ростом концентрации уменьшается степень диссоциации, и при достижении определенной концентрации число ионов в растворе начинает увеличиваться медленнее, чем концентрация. В бесконечно разбавленных растворах слабых электролитов сте-пень диссоциации электролитов невелика, приблизительно α<0,03. С повышением концентрации раствора степень диссоциации электролита уменьшается, что практически не влияет на количество носителей тока.
Кроме того, с возрастанием концентрации электролита в растворе увеличивается его вязкость, что уменьшает подвижность ионов (с↑→η↑→u↓). Поэтому зависимости удельной электропроводности растворов электролитов от их концентрации обычно имеют максимум, см. рисунки (5.5.5) и (5.5.11).
Из анализа приведённых зависимостей, рисунок 5.5.11, можно отметить, что положение максимума будет выше у кислот, затем у оснований, и ниже у солей, что объясняется их наименьшим температурный
коэффициентом. Качественные зависимости κ = f(с) для растворов

951
электролитов ряда: H2SO4, КOH, KCl, CH3COOH будут располагаться так, как приведены на рисунке 5.5.11. Для объяснения свойств ионов в растворах используют значения предельных электрических подвижностей ионов в данном растворителе при данной температуре, численные значения которых для водных растворов приведены в таблице 3.
Таблица 5.5.2 – Предельные молярные подвижности ионов в водных растворах при 25 °С
Из анализа приведенных в таблице 5.5.2 данных можно отметить, что у большинства ионов предельные подвижности изменяется в интервале: (30÷80)·104 См·м2·моль–1. Значительно большую подвижность имеют ионы Н+ (Н3О+) и ОН–. Их подвижности выражаются трехзначными числами: 349,8 и 198,3. Подвижности гидроксония и гидроксид-иона настолько больше подвижностей остальных видов ионов, что это не может быть объяснено с позиций обычной теории Кольрауша. Для катиона водорода подвижность не просто высокая, а, можно сказать, рекордно высокая ≈ 350·10–4 См·м2·моль–1. В 9 раз выше, чем у иона лития, в 7 раз выше, чем у иона натрия (таблица 5.5.2). Как известно, ионов H+ в воде нет, а есть положительные ионы гидроксония H3O+. Ионы H3O+ в свою очередь могут объединяться с молекулами воды, образуя ассоциат-ионы: H5O2+, H7O3+, H9O4+.
Размеры иона гидроксония Н3О+ не меньше, чем размеры других ионов, следовательно, нет оснований полагать, что они двигаются в вязкой среде растворителя быстрее других ионов.
Для объяснения высокой электрической проводимости кислот и щелочей Теодор фон Гротгус в 1806 году предложил «эстафетный» механизм передачи протона в кислой среде с ионов гидроксония на молекулы воды, а в щелочной – с молекул воды на гидроксид-ионы, по которому перемещение ионов протона и гидроксила продолжается по цепи. Передача иона водорода по цепочке связанных водородными связями молекул воды проходит в несколько стадий и практически скорость «движения протонов в

952
растворителе» определяется скоростью поляризации молекул растворителя. Под действием электрического поля ион гидроксо-ния передаёт протон по водородной связи молекуле воды ближайшего ассоциата. Эстафетный механизм передачи заряда приведён на рисунке 5.5.12.
Рисунок 5.5.12 – Схема передачи заряда протона
В результате эстафетного движения под действием внешнего электрического поля ассоциат приобретает избыточный положительный заряд, который он передаёт соседнему ассоциату, отдавая протон от ближайшей к нему молекулы воды вдоль силовых линий (по направлению) электрического поля к отрицательному полюсу.
Перемещается не сам ион H3O+, а протон, перескакивая с одной молекулы воды на другую, переносит с собой положительный заряд (рисунки 5.5.12, 5.5.13). В результате такого перескока протон проходит 0,86 Ǻ, что отвечает перемещению катиона гидроксония на 3,1 Ǻ, или перенос гидроксила в электрическом поле к аноду.
Аналогично происходит перемещение под воздействием электрического тока иона гидроксила к положительному полюсу путем отщепления им протона от молекулы воды ближайшего ассоциата (рисунки
5.5.12, 5.5.13).
Рисунок 5.5.13 – Схема передачи заряда

953
Однако подвижность иона гидроксила меньше, чем иона Н3О+, так как протон в ионе Н3О+ связан менее прочно, чем в молекуле воды. Кроме того, протон водорода передаётся вдоль силовых линий электрического поля, а ион OH– – против.
В неводных растворителях, где невозможен «эстафетный» ме-ханизм движения, ионы Н+ и ОН– не перемещаются с аномально большими скоростями.
Зависимости, представленные на рисунках 5.5.5 и 5.5.11 используют в производственной практике для подбора электролитов с наибольшей электропроводностью, применение которых позволяет экономить электроэнергию.
Радиус и заряд иона. Радиус (ri) и заряд (zi) иона – это два параметра, которые определяют природу иона и его подвижность. Движение иона, как макроскопического шарика в вязкой среде можно описать формулой Стокса (26), из которой следует, что скорость движения ионов обратно пропорциональна их радиусу. При движении в растворе на ион с одной стороны будет действовать сила сопротивления, величина которой описывается выражением (5.5.25):
(5.5.25)
где Fсопр – сила сопротивления среды при движении шарообразной частицы; η – вязкость среды; ri – радиус иона; ui – скорость движения иона.
С другой стороны, сила перемещающая ион в растворе пропорциональна действию электрическая поля на него (формула 5.5.26):
(5.5.26)
где zi – заряд иона; E – напряжённость электрического поля; e – заряд электрона.
При равновесии обе силы можно приравнять (Fсопр = Fэл) и представить следующее равенство (формула 5.5.27):
(5.5.27)
Преобразуем уравнение (5.5.27), поделив обе его части на напряжённость поля (Е) и введя замену (ui/Е) на (ui) (формула 5.5.28):
(5.5.28)
Умножим равенство (5.5.28) на число Фарадея (F) и перейдём от (ui·F) к величине λi (формула 5.5.29):
(5.5.29)

954
Выразим из (5.5.29) зависимость подвижности иона от величины радиуса (формула 5.5.30):
(5.5.30)
Из выражения (5.5.30) следует, что с уменьшением радиуса иона (ri↓) его подвижность возрастает (λi↑). Однако, полученная закономерность не учитывает явление гидратации ионов.
Рассмотрим ряд однозарядных ионов – Li+, Na+, К+, Rb+, Cs+ – в которых последовательно возрастают истинные ионные радиусы. Можно предположить, что с повышением радиуса иона (ri) в этом ряду должна понижаться скорость его движения в растворе. Однако, данные предельных молярных подвижностей ионов этого ряда в водных растворах при 25 °С, (таблица 5.5.2) противоречат нашим рассуждениям. Подвижность ионов увеличивается при переходе от иона Li+ к K+ почти в два раза. Это объясняется тем, что в растворе ионы не свободны, а гидратированы. То есть, ионы в ионной решётке и в растворе обладают разными радиусами. При этом, чем меньше истинный (кристаллохимический) радиус иона, тем больше его эффективный радиус (определяется степенью его гидратации) в растворе электролита (рисунок 5.5.14).
Рисунок 5.5.14 – Закономерности из менения параметров ионов
Сильно гидратированный ион Li+ движется между молекулами воды в электрическом поле гораздо медленнее, чем менее гидратированный ион Cs+. Например,
 См·см2·моль–1.
См·см2·моль–1.
Чем выше заряд иона (zi+) и тем более сильное электрическое поле он имеет. Тем сильнее ионы противоположного знака притягиваются к нему.
Вокруг иона формируется ионная (гидратная) атмосфера за счёт иондипольной связи ионов этого ряда с молекулами воды.
Ион Li+ имеет более сильное электрическое поле, так как его удельный заряд (отношение величины заряда частицы к её массе) больше, чем у других

955
щелочных ионов, поэтому в растворе он и гидратируется интенсивнее. Влияние параметров заряда и радиуса иона взаимосвязано, но неоднозначно: чем выше величина заряда и меньше радиус иона, тем сильнее гидратируется ион, толще гидратная оболочка и, следовательно, тем ниже подвижность иона в растворе. Наибольшая гидратная оболочка у иона Li+. Радиус гидратированного иона уменьшается по направлению к иону Cs+, согласно риунка 5.5.14.
На рисунке 5.5.15 представлены кривые радиусов ионов и скорости их движения при напряжённости электрического поля 1 В/м.
Рисунок 5.5.15 – Сопоставление радиусов ионов щелочных металлов в кристаллической решетке (пунктирная линия) со скоростью их движения (сплошная
линия) в водном растворе при напряженности поля 1 В/м
Увеличение скорости ионов в водном растворе от иона Li+ к Cs+ отражает уменьшение степени гидратации и симбатное повышение их подвижности.
5.5.4 Электрохимическое равновесие на границе раздела фаз
Скачок потенциала ‒ возникает в результате пространственного разделения заряда, обусловленного переходом заряженных частиц на границе раздела фаз Возникающее электрическое поле, влияет на химические процессы, которые могут протекать на межфазной границе, а химические процессы, в свою очередь, могут изменить величину скачка потенциалов.

956
Металл – вакуум. Электрон свободен только в границах металла. Отдельные электроны с достаточно большой кинетической энергией могут выйти из металла в окружающее свободное пространство (в вакуум). При переходе электроном границы «металл-вакуум» возникает кулоновская сила притяжения между электроном и образовавшимся на поверхности избыточным положительным зарядом. Вблизи поверхности возникает «электронное облако», которое вместе с поверхностным слоем положительных ионов образует двойной электрический слой толщиной 10– 10–10–8 м (рисунок 5.5.16). Поле этого слоя препятствует выходу следующих электронов.
Рисунок 5.5.16 – Скачок потенциала на границе раздела фаз «металл–вакуум»
При переходе границы «металл-вакуум» электроны совершают работу против сил притяжения со стороны избыточного положительного заряда, возникшего в металле после их выхода, и против сил отталкивания от ранее вышедших электронов.
Работа выхода Wвых – работа, которую нужно совершить для удаления электрона из металла в вакуум (формула 5.5.31):
(5.5.31)
где е – заряд электрона, χ – поверхностный потенциал. Размерность [Wвых] = эВ (электрон-вольты).
1эВ – работа перемещения электрона в электрическом поле между точками с разностью потенциалов в 1В (1эВ =1,6·10-19 Дж).
Поверхностный потенциал χ характеризует падение потенциала в заряженном поверхностном слое. Поверхностный потенциал (χ) –

957
потенциал, который связан с работой переноса элементарного воображаемого заряда из глубины фазы в точку в вакууме, расположенную в непосредственной близости от поверхности фазы (на расстоянии 10-10–10-9 м) без учета взаимодействия с самой фазой (рисунок 5.5.17).
Рисунок 5.5.17 – Поверхностный, внешний и внутренний потенциалы на границе раздела фаз «металл–вакуум»
Внешний потенциал (ψ) – это потенциал, который определяется работой переноса элементарного воображаемого заряда в вакууме из бесконечности в точку, расположенную в непосредственной близости от поверхности данной фазы (на расстоянии 10–10–10–9 м); Внутренний потенциал (φ) – потенциал, который соответствует работе переноса элементарного воображаемого заряда из бесконечности в вакууме вглубь данной фазы (формула 5.5.32).
(5.5.32)
Металл – металл. Между двумя изолированными кусками металла устанавливается произвольная разность потенциалов, значение которой зависит от случайного накопления избыточных зарядов на их поверхности
(рисунок 5.5.18).
Рисунок 5.5.18 – Скачок потенциала на границе раздела фаз «металл–металл»
При соприкосновении металлов заряды перераспределятся и потенциалы выровняются.
В случае одинаковых металлов выравнивание будет полным, а в случае металлов различной природы на границе установится определённая разность

958
потенциалов (Гальвани-потенциал) , зависящая от природы проводников
(формула 5.5.33):
(5.5.33)
Контактная разность потенциалов зависит от соотношения в способности металлов отделять электроны и равна разности работ выхода электрона.
Энергетическое состояние заряженных частиц в электрохимической системе. Каждая і-тая частица фазы обладает химическим потенциалом – энергией взаимодействия частицы внутри фазы с частицами, образующую эту фазу (формула 5.5.34):
(5.5.34)
Электрохимический потенциал характеризует энергетическое состояние заряженной частицы, при котором учитывается как электрическая, так и химическая работа переноса (формула 5.5.35):
(5.5.35)
где  – электрохимический потенциал i-й заряженной частицы в фазе; μi – химический потенциал; zi– заряд частицы; φi– внутренний потенциал частицы; F – постоянная Фарадея (F = 96487 Кл/моль).
– электрохимический потенциал i-й заряженной частицы в фазе; μi – химический потенциал; zi– заряд частицы; φi– внутренний потенциал частицы; F – постоянная Фарадея (F = 96487 Кл/моль).
Электрохимическое равновесие при переносе частицы через границу раздела фаз. Согласно уравнению Гиббса-Дюгема (формула 5.5.36):
(5.5.36)
При переносе заряженной частицы через границу раздела фаз:
qi – заряд, а dqi = zi Fdni , поэтому

959
Равновесие заряженных частиц в двухфазной системе характеризуются равенством их электрохимических потенциалов.
Причины возникновения скачка потенциала на границе раздела фаз:
Обмен заряженными частицами;
Избирательная адсорбция;
Адсорбция полярных молекул;
Наличии внешнего источника тока (случай идеально поляризуемых электродов).
Равновесный электродный потенциал. На границе раздела металл-
раствор устанавливается динамическое равновесие (рисунок 5.5.19):
Рисунок 5.5.18 – Динамическое равновесие на границе раздела фаз «металл– раствор»
Равновесный потенциал электрода ‒ разность (скачок) потенциала между электродом и раствором, который устанавливается при одинаковых скоростях прямой и обратной электродных реакций.
Для электродной реакции Ox + ne– Red в состоянии равновесия (формула 5.5.37)

960
(5.5.37)
Согласно уравнению изотермы Вант-Гоффа для химической реакции
(формула 5.5.38):
(5.5.38)
E0 – стандартный электродный потенциал
Физический смысл E0: если a(Ox) = a(Red) = 1 моль/л, то Е = E0
Уравнение Нернста:
При нормальной температуре (Т = 298 К) с учетом численных значений постоянных величин уравнение Нернста может быть преобразовано следующим образом:
Абсолютное значение электродного потенциала определить невозможно!
На практике используют разность потенциалов исследуемого электрода и некоторого стандартного электрода сравнения
Для водных растворов в качестве электрода сравнения используют
стандартный водородный электрод.
Потенциал стандартного водородного электрода при всех температурах принят равным нулю.

961
Стандартный электродный потенциал Е° электрода равен стандартной ЭДС электрохимической цепи, составленной из исследуемого электрода и стандартного водородного электрода
При схематическом изображении цепи водородный электрод записывают слева, а исследуемый электрод – справа:
Стандартная э.д.с. элемента Даниэля-Якоби
5.5.5 Классификация электродов и электрохимических цепей
Различают:
-Электроды первого рода;
-Электроды второго рода;
-Газовые электроды;
-Окислительно-восстановительные электроды (Red-Ox);
-Ионселективные электроды.
Электрод первого рода ‒ полуэлемент, состоящий из металла или неметалла, погруженного в раствор, содержащий его ионы. Схема электрода, согласно IUPAC:
-для металла: Mz+|M
-для металлоида: Mеz-|Mе
Потенциал определяющие реакции (записываются в форме реакций восстановления):
-для металла: Mz++ zе = M
- для металлоида: Mе + ze = Mеz‒ Например:
1. Медный электрод Cu2+|Cu0 (E0 = +0.337 B); Cu2+ +2e Cu0 ;
Активность твердой фазы – const (входит в Е0), потенциал от нее не зависит, поэтому уравнение упрощается:
2. Селеновый электрод Se2–|Se0 (E0 = – 0.92 B); Se0 + 2e Se2– ;

962
Электрод второго рода ‒ полуэлемент, состоящий из металла, покрытого слоем его малорастворимого соединения и погружённого в раствор растворимой соли, содержащей тот же анион, что и малорастворимое соединение.
Схема электрода: Me|MeA, Az-
Потенциал определяющая реакция: MeA + ze Me + Az– Потенциал электрода:
В электрохимической реакции ионизируется металл, а потенциал определяется концентрацией анионов его малорастворимого соединения.
Электроды второго рода – электроды сравнения (рисунок 5.5.19):
1. Хлорсеребряный (хлоридсеребряный) электрод Ag|AgCl, Cl–
Реакция: AgCl + e Ag0 + Cl–
Потенциал определяющая реакция: Ag+ + e Ag0 Запишем уравнение Нернста:
Потенциал электрода определяется концентрацией (активностью) ионов серебра в растворе, образующихся в результате диссоциации малорастворимой соли AgCl:
Активность катиона определяется произведением растворимости данной соли:
Подставляем в уравнение Нернста:

963
Отсюда:
При 298 К:
Величина Е зависит только от концентрации (активности) аниона, который не принимает участие в окислительно-восстановительной полуреакции, т.е. его концентрация остается постоянной при данной температуре, что позволяет использовать его как электрод сравнения.
Пересчет потенциалов, измеренных относительно насыщенного хлорсеребряного электрода сравнения φ (vs. н.х.с.) в водородную шкалу φ (vs.
н.в.э.):
2. Каломельный электрод Hg|Hg2Cl2, Cl–
Реакция: 1/2 Hg2Cl2Hg+ + Cl –
Потенциал определяющая реакция: Hg+ + e Hg0 Уравнение Нернста:

964
Электродный потенциал при T = 298 K:
Рисунок 5.5.19 – Электроды второго рода – электроды сравнения
3. Оксидно-ртутный электрод Hg, HgO|OH–
Реакция: 1/2 Hg2Cl2 Hg+ + Cl –
Потенциал определяющая реакция: HgO + H2O + 2 e 2OH– + 2Hg0 Роль анионов малорастворимых соединений играют гидроксид-ионы
OH–.
Электродный потенциал при T = 298 K:
Газовые электроды:
1.Водородный электрод H+| H2 | Pt (рисунок 5.5.20)
Потенциал определяющая реакция: 2H+ + 2e H2
Уравнение Нернста для расчета потенциала водородного электрода:

965
При РН2 = 1атм и температуре Т = 298 K
Примечание: (1) Pt черненная, (2) газообразный H2, (3) 0,5М р-р H2SO4 (а(Н+) = 1 моль/л)
Рисунок 5.5.20 – Водородный электрод
Водородный электрод:
-Индикаторный электрод для измерения РН
-Электрод сравнения при + = 1, =1 атм
2. Кислородный электрод OH–|O2|Pt
Потенциал определяющие реакции:
вкислой среде: O2 + 4H+ + 4e 2H2O
вщелочной среде: O2 + 2H2O + 4e 4OH –
Потенциал кислородного электрода зависит от рН:

966
Окислительно-восстановительный электрод ‒ система, состоящая из индифферентного металла (платины), погруженного в раствор, содержащий окисленную и восстановленную форму вещества.
Например: Red-Ox электрод Pt|Sn4+, Sn2+
Потенциал определяющая реакция: Sn4+ + 2e Sn2+
Правило Лютера: Систему, состоящую из металла М в растворе, содержащем ионы этого металла в двух степенях окисления Мz1+ и Мz2+ можно представить, как совокупность трех систем:
Для электродов I рода справедливы следующие соотношения:
Для окислительно-восстановительного электрода:
Например: Ионизация Fe до Fe3+ может проходить либо ступенчато – через промежуточную степень окисления, либо непосредственно – до крайней степени окисления, причем изменение свободной энергии процесса не зависит от его пути (закон Гесса):

967
Ионселективные электроды ‒ в электродной реакции которых не участвуют электроны, потенциалы определяются процессами распределения ионов между мембраной и раствором.
Стеклянный электрод Ag, AgCl| 0,1M HCl | стекл. мембрана| Н+
При помещении стеклянного электрода в раствор в поверхностный слой стекла из раствора интенсивно проникают ионы водорода, вытесняя ионы Nа+ или Li+ , содержащиеся в стекле.
Ионы водорода распределяются между стеклом и раствором и на границе раздела фаз возникает разность потенциалов.
Т. к. переход ионов водорода в стекло зависит от концентрации их в растворе, то потенциал стеклянного электрода зависит от рН раствора.
Электрохимические цепи. Основные понятия:
Электрод (полуэлемент) – проводник первого рода, находящийся в контакте с проводником второго рода (электролитом).
Электрохимическая система (электрохимическая цепь) – система,
состоящая из проводников первого рода (металлы, полупроводники), находящихся в контакте с проводником (или проводниками) второго рода.
Электролитическая ячейка (электролизер) – электрохимическая система, в которой химические превращения совершаютсяза счет внешней электрической энергии.
Гальванический элемент (химический источник тока) –
электролитическая система, генерирующая электрическую энергию за счет самопроизвольно происходящих в ней химических превращений.
В гальванических элементах источником электрической энергии является энергия Гиббса протекающих в системе окислительновосстановительных реакций (ОВР).
Гальванический элемент – электрохимическая система, состоящая из двух электродов, в которой протекает самопроизвольная окислительновосстановительная реакция, и в результате которой происходит превращение химической энергии в электрическую.
Гальванические элементы – химические источники тока.

968
Реакции окисления и восстановления протекают на разных электродах, т.е. пространственно разделены.
Анод (+) – электрод, на котором происходит окисление (отдача ē ) Катод (-) – электрод, на котором происходит восстановление
(присоединение ē)
Електродвижущая сила (ЭДС) – предельная разница потенциалов, возникающая на границе раздела фаз в разомкнутой цепи элемента
ЭДС равна разности потенциалов электродов:
Е = Ек – Еа
ЭДС – количественная характеристика эффективности работы гальванического элемента – отражает полноту процесса перехода химической энергии в электрическую.
Е величина всегда положительная (Е > 0).
Электродные реакции в гальваническом элементе Даниэля-Якоби:
Окислительно-восстановительная реакция:
СuSO4 + Zn = ZnSO4 + Cu Cu2+ + Zn = Zn2+ + Cu
На границах раздела фаз металл-раствор протекают процессы (рисунок
5.5.21):
Анод: Zn - 2e ↔ Zn2+ Катод: Cu2+ + 2e ↔ Cu
Рисунок 5.5.21 – Электродные реакции в гальваническом элементе ДаниэляЯкоби
Электроны движутся по внешней цепи, по проводнику, который соединяет два электрода
Движение потока электронов по проводнику и есть электрический ток.
Классификация электрохимических цепей:

969
1.Физические (аллотропические и гравитационные): электроды одинаковой химической природы в одном и том же растворе.
2.Концентрационные: идентичные по природе и состоянию электроды - в растворах с разными концентрациями окисленной или
восстановленной форм (цепи с переносом – имеется диффузионный скачок потенциала);
-в одном и том же растворе (цепи без переноса – например, с газовыми электродами при разных давлениях или с амальгамными электродами разной концентрации).
(в этих цепях не протекает химических реакций) 3. Химические (с переносом и без переноса): в цепи протекает
химическая реакция.
Цепь равновесна, если:
-установлены равновесия на обоих электродах;
-разность потенциалов электродов скомпенсирована разностью потенциалов от внешнего источника.
Пример химической цепи без переноса – Элемент Вестона (рисунок
5.5.22).
Рисунок 5.5.22 – Элемент Вестона (химическая цепь без переноса; 1.0183 В при 20 С)
5.5.6 Практическое применение метода измерения ЭДС гальванических элементов. Потенциометрия
Потенциометрия – метод определения термодинамических характеристик и физико-химических свойств химических систем и химических процессов на основе измерения ЭДС электрохимических цепей.

970
Потенциометрическим методом могут быть определены константы равновесия и термодинамические функции химических реакций, коэффициенты активности электролитов, pH растворов, произведение растворимости. Метод широко используется для аналитических целей.
Определение константы химического равновесия. Для определения константы равновесия химической реакции необходимо составить гальванический элемент, в котором эта реакция могла бы быть осуществлена. Расчет константы равновесия проводится в соответствии с уравнением (5.5.37) на основании значения стандартной ЭДС элемента Eo , определяемой как разность стандартных потенциалов положительного (E02) и отрицательного ( E01 ) электродов (формула 5.5.39):
(5.5.39)
где Kо – стандартная (термодинамическая) константа равновесия химической реакции; z – число электронов, проходящих через электрохимическую цепь при однократном протекании реакции (одном пробеге реакции).
Расчет термодинамических функций химических реакций. Для расчета термодинамических функций химической реакции измеряют ЭДС гальванического элемента при различных температурах иопределяют температурный коэффициент ЭДС, т.е. величину
Термодинамические функции реакции, протекающей в элементе при заданной T, рассчитывают по формулам (5.5.40), (5.5.41), (5.5.42).
(5.5.40)
(5.5.41)
(5.5.42)
Определение активностей и коэффициентов активности.
Определение активностей и коэффициентов активности электролита удобно проводить с использованием электрохимической цепи без переноса, один из электродов которой обратим по катиону, другой – по аниону.
Пусть требуется определить активность и средний ионный коэффициент активности сильного электролита M + A -. Для этого составим гальванический элемент из электродов 1-го и 2-го рода, обратимых

971
соответственно по катиону Mz+ и аниону Az- и погруженных в раствор электролита заданной концентрации m:
На электродах протекают следующие процессы
Суммарная реакция, с учетом того, что
:
Принимая во внимание, что активности чистых фаз
и
получаем следующее выражение для ЭДС элемента (формула 5.5.43):
(5.5.43)
Индивидуальные активности ионов, средние ионные активности, активность и моляльность электролита M + A - связаны уравнениями (5.5.44 и
25.45):
(5.5.44)
(5.5.45)
Подстановка выражений (5.5.44) и (5.5.45) в уравнение (5.5.43) дает выражение 5.5.46:
(5.5.46)
Дальнейший ход определения a, a± и γ± зависит от того, известны или нет величины стандартных электродных потенциалов.
Величины стандартных электродных потенциалов известны
Определяя экспериментально ЭДС элемента и используя значения стандартных потенциалов электродов 1-го и 2-го рода, по уравнениям (11.2), (11,3) и (11.4) вычисляют величины a, a± и γ± электролита.
Величина стандартной ЭДС (Eo) неизвестна
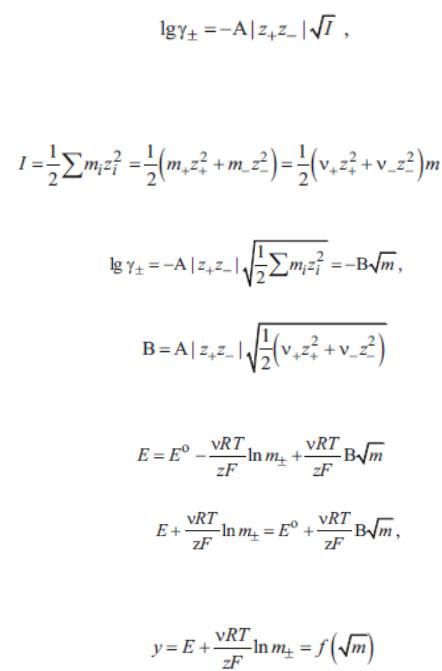
972
Cначала необходимо экспериментально определить величину Eo. Для достаточно разбавленных растворов (I ≤ 0,01) справедливо уравнение предельного закона Дебая–Хюккеля (формула 5.5.47):
(5.5.47)
где A = f (ԑ, T), z+ и z- – зарядовые числа ионов, I – ионная сила раствора.
Ионную силу раствора, содержащего электролит M + A - с моляльной концентрацией m, вычисляют по формуле (5.5.48):
(5.5.48)
Тогда уравнение предельного закона Дебая–Хюккеля принимает вид
(5.5.49):
(5.5.49)
где
После подстановки (5.5.49) в уравнение (5.5.46) имеем выражение
(5.5.50):
или
(5.5.50)
Измеряя ЭДС цепи при различных концентрациях электролита (рисунок 5.5.23), строят график зависимости

973
Рисунок 5.5.23 – К определению величины стандартной ЭДС гальванического элемента
В области разбавленных растворов, где выполняется предельный закон Дебая–Хюккеля, экспериментальная зависимость y = f( ) принимает линейный характер. Экстраполируя эту зависимость к моляльной концентрации m→0, определяют величину стандартной ЭДС (пересечение линейного участка кривой y = f(
) принимает линейный характер. Экстраполируя эту зависимость к моляльной концентрации m→0, определяют величину стандартной ЭДС (пересечение линейного участка кривой y = f(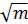 ) с осью ординат).
) с осью ординат).
Используя найденное значение Eo, далее по уравнению (11.5) рассчитывают значение среднего ионного коэффициента активности для заданной концентрации электролита.
На рисунке 5.5.23 показано определение стандартной ЭДС для элемента Pt, H2 |HCl |AgCl |Ag | Pt . Как видно из графика, Eo = 0,222 B, что отвечает значению стандартного потенциала хлорсеребряного электрода.
Определение pH растворов. К числу наиболее распространенных приложений потенциометрического метода относится определение рН среды. Для измерения рН растворов составляют гальваническую цепь из индикаторного электрода (потенциал которого зависит от рН) и электрода сравнения. В качестве индикаторных электродов обычно используют водородный, хингидронный или стеклянный электроды.
Определение pH раствора с помощью водородного электрода.
Индикаторным электродом в данном случае служит водородный электрод. При использовании в качестве вспомогательного электрода, например, насыщенного каломельного электрода, схема измерительной цепи запишется следующим образом:
ЭДС составленной цепи рассчитывается как разность потенциалов насыщенного каломельного и водородного электродов (диффузионный потенциал должен быть устранен). При 298 K будем иметь:
Откуда получаем выражение (5.5.51):

974
Работа с водородным электродом сопряжена с трудностями, вследствие чего его редко применяют индикаторного электрода для измерения pH растворов.
Определение pH раствора с помощью хингидронного электрода
Потенциал хингидронного электрода в кислых и слабощелочныхсредах является линейной функцией pH раствора. Схема электрической цепи для измерения pH раствора с хингидронным электродом и каломельным электродом сравнения (0,1 M KCl) имеет вид:
ЭДС приведенной цепи при 298 K:
откуда получаем выражение (5.5.52):
(5.5.52)
Несомненными достоинствами хингидронного электрода являются быстрое установление равновесного значения электродного потенциала, простота аппаратурного оформления и отсутствие необходимости в калиб ровке электрода. К практическим недостаткам хингидронного электрода относится ограниченная область pH, в которой он дает достоверные значения (pH=0–8). При pH ≥ 8 гидрохинон ведет себя как слабая двухосновная кислота, в результате диссоциации которой в растворе увеличивается концентрация ионов водорода, а потенциал электрода принимает более положительные значения (формула 5.5.53).
(5.5.53)
Другим недостатком хингидронного электрода является его восприимчивость к наличию в анализируемой системе окислителей и восстановителей, поскольку в таких средах происходит или окисление гидрохинона в хинон, или восстановление хинона до гидрохинона. Вследствие этого не выполняется равен-ство активностей хинона и гидрохинона в водном растворе (аQ = аQH2) и расчет pH по уравнению (5.5.52) будет неточен.
Определение pH раствора с помощью стеклянного электрода
При измерениях pH растворов в лаборатории или на производстве, как правило, используется стеклянный электрод, который (в качестве индикаторного электрода) послужил основой для создания pН-метра – прибора для определения рН среды.

975
В рН-метре стеклянный электрод, как правило, сочетают с хлорсеребряным или каломельным электродами сравнения. Измерительная схема электрохимической цепи pH-метра выглядит следующим образом:
ЭДС электрохимической цепи pH-метра при 298 K (формула 5.5.54):
(5.5.54)
Отсюда получаем выражение для расчета pH:
Поскольку потенциал электрода сравнения есть величина постоянная, то в общем случае уравнение (5.5.40) принимает вид (формула 5.5.55):
(5.5.55)
где const включает E0cт и потенциал используемого электрода сравнения.
Достоверные экспериментальные данные по определению pH растворов с использованием рН-метра получают в диапазоне pH от 0 до 12. В этом диапозоне потенциал электрода линейно падает с увеличением pH раствора (Рисунок 25). Вне этого интервала водородная функция стеклянного электрода существенно искажается. В сильнощелочных средах стеклянный электрод, приобретает OH-функцию, т.е. является чувствительным к изменениям pH раствора, с той только разницей, что производная
меняет знак c отрицательного на положительный, а на кривой Е=f(pH) возникает экстремальная точка. В сильнокислых растворах из-за амфотерности SiO2 стеклянный электрод проявляет основные свойства и изменение потенциала электрода от кислотности среды при низких рН отклоняется от линейной зависимости (рисунок 5.5.24).

976
Рисунок 5.5.24 – Зависимость потенциала стеклянного электрода от pH раствора
Достоинством стеклянного электрода является достаточно быстрое установление равновесного значения потенциала, величина которого не искажается присутствием в растворах окислителей и восстановителей, солей тяжелых металлов, электродных ядов (сернистых, мышьяковистых и иных соединений) и органических соединений. В равной мере стеклянный электрод можно использовать для измерения водородного показателя в окрашенных и мутных средах.
Определение произведения растворимости
Потенциометрический метод позволяет находить произведение растворимости Ks и растворимость S (концентрацию насыщенного раствора) малорастворимых соединений, в первую очередь, солей и оснований. Для этих целей могут быть использованы различные электрохимические цепи.
Определение Ks с помощью химических элементов без переноса
Использование химических цепей без переноса позволяет непосредственно определять произведение растворимости малорастворимого электролита. Рассмотрим определение Ks на примере соли AgCl , которая водном растворе лишь в малой степени диссоциирует на ионы Ag+ и Cl-.
Составляем соответствующий элемент без переноса:
в котором протекают следующие электродные реакции (z = 1) :
Суммарная реакция:
Экспериментально определенная величина ЭДС приведенного элемента без переноса при 298 K составляет E = 1,136 B и не зависит от концентрации KCl в растворе.

977
Получим уравнение для расчета ЭДС данного элемента как разность потенциалов хлорного и хлорсеребряного электродов. При этом последний удобно представить, как обратимый по катионам (5.15). В этом случае:
Поскольку aAg+·aCl- = Ks,AgCl , получаем выражение (5.5.56):
(5.5.56)
откуда определяем произведение растворимости AgCl при T = 298 K. Справочные величины стандартных потенциалов серебряного и
хлорного электродов равны:
Е0Ag+ /Ag =0,779 B, E0 Cl2 /Cl- = 1,360 B. Тогда:
Справочная величина:
Для расчета растворимости AgCl в чистой воде (SAgCl) без большой ошибки можно принять γ±,AgCl =1. Получаем:
Определение Ks с помощью химических элементов с переносом
В химическом элементе с переносом один электрод должен быть обратимым по одному из ионов малорастворимого соединения, а второй электрод – электродом сравнения. Для определения Ks, AgCl удобно использовать электрохимическую цепь, для которой диффузионный потенциал сведен к минимуму:
Измерение ЭДС приведенной цепи при 298 K дает E = 0,0456 В. Вычисляем потенциал хлорсеребряного электрода:
Записываем уравнение Нернста для хлорсеребряного электрода как обратимого по ионам серебра (формула 5.5.57):
(5.5.57)

978
Далее делаем допущение, что активность ионов хлора в растворе равна средней ионной активности KCl:
Значение среднего ионного коэффициента активности KCl для концентрации m = 0,1 моль/кг берем из справочника: γ±,КCl = 0,770.
Из уравнения (5.5.58) при 298 K находим Ks,AgCl :
Расчет Ks, AgCl на основании значений стандартных электродных
потенциалов Еo Cl- ,AgCl /Ag и ЕoAg+ /Ag .
Электроды 2-го рода обратимы как по анионам, так и по катионам малорастворимого электролита. Уравнение (5.17), устанавливающее связь произведения растворимости малорастворимого соединения с величинами стандартных потенциалов электродов 1-го и 2-го рода, обратимых по ионам этого соединения.
В случае малорастворимого соединения AgCl это уравнение будет содержать стандартные потенциалы серебряного Ag+ |Ag и хлорсеребряного Cl- |AgCl |Ag электродов:
Решая это уравнение относительно Ks, AgCl , получаем:
Таким образом, все рассмотренные методы дают величины Ks, AgCl близкие к справочному значению.
Расчет ионного произведения воды. В водном растворе любого электролита всегда присутствуют и ионы водорода H+, и ионы гидроксила OH- . Поэтому водородный электрод, помещенный в такой раствор, может рассматриваться обратимым одновременно и по H+, и по OH- ионам, а для расчета потенциала электрода применимо как уравнение (5.5.58), так и (5.5.59). Расчет ионного произведение воды Kw проводится в соответствии с уравнением (5.5.60):
(5.5.58)

979
(5.5.59)
(5.5.60)
Переходя к десятичным логарифмам при 298K будем иметь:
Подставляя в это выражение значения стандартных потенциалов водородного электрода в щелочной и кислой средах, при 298 K получаем:
Определение чисел переноса ионов. Для нахождения чисел переноса ионов в растворе используется метод, основанный на измерении ЭДС концентрационных цепей с переносом.
Если требуется, например, определить числа переноса ионов Az- и Mz+ для электролита M +A -, то составляется соответственно либо концентрационная катионная цепь с переносом типа, либо анионная цепь типа.
Тогда число переноса аниона Az- вычисляется по уравнению (5.5.61):
(5.5.61)
а число переноса катиона Mz+ – по уравнению (5.5.62):
(5.5.62)
при условии, что известны значения средних ионных коэффициентов активности или непосредственно средних ионных активностей данного электролита в обоих контактирующих растворах. При этом концентрации двух растворов m1 и m2 не должны сильно различаться, так как числа

980
переноса ионов зависят от концентрации электролита. Определенные из эксперимента числа переноса будут отвечать некоторой средней концентрации m.
Поскольку числа переноса катиона и аниона связаны между собой выражением t+ + t- = 1, то определив число переноса одного из ионов электролита, легко рассчитать и число переноса второго иона.
Для нахождения чисел переноса ионов вовсе не обязательно заранее знать средние ионные коэффициенты активности электролита. Действительно, если, например, сопоставить уравнение (5.5.63) для напряжения разомкнутой катионной концентрационной цепи с переносом (J), составленной из двух водородных электродов с электролитом HCl, и уравнение (5.5.64) для ЭДС сдвоенной цепи (H) с тем же электролитом, то получаем выражение, позволяющее определить число переноса аниона:
(5.5.63)
(5.5.64)
где E(J) – напряжение катионной цепи с переносом (J), E(H) – разность потенциалов на концах сдвоенной цепи (H).
Подчеркнем, что в обеих цепях протекает один и тот же суммарный процесс HCl(a2) → HCl(a1).
Из уравнений Нернста для анионной концентрационной цепи (L) (5.5.65) и сдвоенной цепи (G) (5.5.66), суммарный процесс в которых передается уравнением HCl(a2) → HCl(a1), получаем выражение для числа переноса катиона:
(5.5.65)
(5.5.66)

981
5.6 ОБЩАЯ ХАРАКТЕРИСТИКА И КЛАССИФИКАЦИЯ ДИСПЕРСНЫХ СИСТЕМ. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ. АДСОРБЦИЯ НА ГРАНИЦЕ РАЗДЕЛА ФАЗ. ПОЛУЧЕНИЕ ДИСПЕРСНЫХ СИСТЕМ И ИЗ СВОЙСТВА
ПЛАН
5.6.1 Общая характеристика и классификация дисперсных систем.
5.6.2 Адсорбция на границе раздела фаз.
5.6.3 Адгезия и когезия.
5.6.4 Электрические свойства дисперсных систем.
5.6.5 Получение дисперсных систем и их устойчивость.
5.6.6 Молекулярно−кинетические и оптические свойства дисперсных систем.
5.6.7 Коллоидно-химические основы охраны природной среды.
5.6.1 Общая характеристика и классификация дисперсных систем
Дисперсные системы – гетерогенные системы, состоящие из дисперсионной среды (Д. с.) – растворителя, и дисперсной фазы (Д.ф.) – растворенного вещества.
Характерным свойством дисперсной системы является наличие большой межфазной поверхности, поэтому свойства поверхности для нее являются определяющими.
Для характеристики дисперсной системы используют следующие величины:
1. Поперечный размер частиц дисперсной фазы (а). [а] = м.
2.Дисперсность (Д) – величина, обратная поперечному размеру
частиц:
Д=  , м-1
, м-1
3.Удельная поверхность (Sуд). Это межфазная поверхность (S1,2) в расчете на единицу объема дисперсной фазы (V) или её массы (m):
Для системы, содержащей сферические частицы с радиусом r, получим выражение (5.6.1):
(5.6.1)

982
Для системы с кубическими частицами с ребром ℓ имеем выражение
(5.6.2):
(5.6.2)
В общем случае получаем выражение (5.6.3):
(5.6.3)
где К – коэффициент, зависящий от формы частиц (для сферических и кубических частиц К = 6).
Согласно уравнению, удельная поверхность прямо пропорциональна дисперсности Д и обратно пропорциональна размеру частиц а. С повышением дисперсности (раздробленности) системы Syд резко возрастает.
Классификация дисперсных систем. В основе существующих классификаций лежат различные свойства дисперсных систем. Наиболее распространена классификация дисперсных систем по следующим признакам:
-По размеру частиц дисперсной фазы.
-По агрегатному состоянию дисперсной фазы и дисперсионной среды.
-По степени взаимодействия дисперсной фазы с дисперсионной
средой.
-По наличию взаимодействия между частицами дисперсной фазы.
По размеру частиц дисперсной фазы (таблица 5.6.1): 1. Микрогетерогенные (Грубодисперсные системы)
>10-7м или >100 нм
2.Ультрамикрогетерогенные: коллоидные растворы (золи).
≈10-7 – 10-9 м, 1 – 100 нм
3. Молекулярно-ионнодисперсные: истинные растворы низкомолекулярных соединений (НМС)
< 10-9 м, < 1 нм
Таблица 5.6.1 – Классификация дисперсных систем по размеру частиц дисперсной фазы
Размер |
Название систем |
Основные признаки дисперсных систем |
>10-7м |
Микрогетерогенные |
- гетерогенные; |
|
(грубодисперсные): |
- частицы не проходят через бумажный фильтр и |
|
эмульсии, |
ультрафильтры; |
|
суспензии, |
- частицы видны в оптический микроскоп; |
|
аэрозоли, пены. |
- неустойчивы кинетически и термодинамич.мутные |
10-7 – 10-9 м |
Ультрамикрогетерог |
- гетерогенные; |
|
ен-ные: коллоидные |
- частицы проходят через бумажный фильтр и не |
|
растворы (золи) |
проходят через ультрафильтры; |
|
|
- частицы не видны в оптический микроскоп, видны |
|
|
в электронный микроскоп и ультрамикроскопом; |

983
|
|
- |
относительно |
устойчивы |
кинетически, |
|
|
неустойчивы термодинамически; |
|
||
|
|
- прозрачные, опалесцирующие – рассеивают свет |
|||
|
|
(дают конус Фарадея-Тиндаля) |
|
||
< 10-9 м |
Молекулярноионно- |
- гомогенные; |
|
|
|
|
дисперсные: |
- частицы проходят через бумажный фильтр и |
|||
|
истинные растворы |
ультрафильтры; |
|
|
|
|
низкомолекулярных |
- частицы не видны в современные микроскопы; |
|||
|
соединений (НМС) |
- устойчивы термодинамически и кинетически; |
|||
|
|
- |
прозрачные, не |
дают конус |
Фарадея-Тиндаля |
|
|
(оптически пусты). |
|
|
|
По агрегатному состоянию дисперсной фазы и дисперсионной среды (таблица 5.6.2):
Таблица 5.6.2 – Классификация дисперсных систем по агрегатному состоянию дисперсной фазы и дисперсионной среды
Дисперсионная |
Дисперсная |
Условное |
Примеры |
среда |
фаза |
обозначение |
дисперсных |
|
|
|
систем |
Газ |
Газ |
Г / Г |
Отсутствует |
(аэрозоли) |
Жидкость |
Ж / Г |
Туман, облака |
|
Твердое тело |
Т / Г |
Дым, пыль, |
|
|
|
порошки |
Жидкость |
Газ |
Г / Ж |
Пена |
(лиозоли ) |
Жидкость |
Ж1 / Ж2 |
Эмульсии |
|
Твердое тело |
Т / Ж |
Взвеси, |
|
|
|
суспензии |
Твердое тело |
Газ |
Г / Т |
Пемза, хлеб |
(солидозоли) |
Жидкость |
Ж / Т |
Почва, грунт |
|
Твердое тело |
Т1 / Т2 |
Минералы,сплавы |
По степени взаимодействия дисперсной фазы с дисперсионной средой (по межфазному взаимодействию) (таблица 5.6.3):
Таблица 5.6.3 – Классификация дисперсных систем по агрегатному состоянию дисперсной фазы и дисперсионной среды
Лиофобные системы: |
Лиофильные системы: |
коллоидные растворы, суспензии, |
растворы коллоидных ПАВ и |
эмульсии, пены, аэрозоли |
высокомолекулярных соединений (ВМС) |
Слабое взаимодействие между Д.ф. и Д.с. |
Сильное взаимодействие между Д.ф.и Д.с. |
|
|
Образуются за счет энергии извне |
Образуются самопроизвольно |
|
|
Термодинамически неустойчивы |
Термодинамически устойчивы |
|
|
Для устойчивости необходим стабилизатор |
Устойчивыбез стабилизатора |
По наличию взаимодействия между частицами дисперсной фазы
(таблица 5.6.4):
984
Таблица 5.6.4 – Классификация дисперсных систем по наличию взаимодействия между частицами дисперсной фазы
Свободнодисперсные системы: |
Связнодисперсные системы: |
||||
лиозоли, суспензии, эмульсии, |
|
студни, пористые |
|||
аэрозоли. |
|
|
|
|
капиллярные системы |
Частицы дисперсной фазы не связаны |
Частицы дисперсной фазы имеют между |
||||
между |
собой |
и |
могут |
свободно |
собой устойчивые связи, образуя сплошную |
перемещаться в |
объеме дисперсионной |
структуру (сетку каркас), внутри которой |
|||
среды. |
|
|
|
|
заключена дисперсионная среда |
Все сложные лекарственные формы по своей природе являются разнообразными дисперсными системами.
При изготовлении решают две основные задачи:
-оптимальное диспергирование лекарственного вещества или нескольких веществ;
-равномерное распределение диспергированного вещества в массе носителя или других компонентов.
Понятия поверхностных явлений. Поверхностные явления имеют место на границе раздела фаз. Реальная межфазовая граница – это поверхностный слой толщиной, не превышающий 1 нм, в пределах которого термодинамические параметры (концентрация компонентов, давление, температу-ра и др.) испытывают резкие изменения. Причина возникновения поверхностных явлений – наличие избыточной поверхностной энергии на поверхности раздела фаз, т.к. молекулы вещества по обе стороны от границы имеют свободные, т.е. ненасыщенные валентности, они-то в совокупности и дают поверхностную энергию (dGS) (формула 5.6.4):
dGS = σ·dSуд |
(5.6.4) |
где σ – поверхностное натяжение; dSуд – удельная поверхность.
Все системы, обладающие избыточной энергией – неустойчивы. Поэтому в дисперсных системах согласно 2 закону термодинамики самопроизвольно идут процессы с понижением dGS. Следовательно, поверхностную энергию можно снизить, уменьшив поверхностное натяжение или удельную поверхность. Поэтому все поверхностные явления тоже можно разделить на две группы:
1)поверхностные явления с уменьшением Sуд, при которых происходит самоукрупнение дисперсных частиц: а) коагуляция; б) коалесценция; в) образование сферических частиц.
2)поверхностные явления с уменьшением σ: адсорбция, адгезия, когезия, смачивание, растекание.
5.6.2 Адсорбция на границе раздела фаз
Поверхностные явления сильнее всего проявляются в системах с очень большой поверхностью раздела фаз. К таким системам относятся

985
поверхностные слои, пленки, нити, капилляры, мелкие частицы. Их совокупность вместе со средой, в которой они находятся, образует
дисперсную коллоидную систему.
Та часть системы, которая находится в измельченном состоянии, называется дисперсной фазой. Сплошная фаза, в которой распределена дисперсная фаза, называется дисперсионной средой.
Большой запас энергии определяет характерную особенность дисперсных коллоидных систем – их неустойчивость.
В живом организме имеет место большое количество поверхностей раздела. Это стенки сосудов, альвеол, поверхности клеток, клеточных ядер, форменных элементов крови, коллоидных частиц и, наконец, поверхности раздела между организмом и окружающей средой.
Самопроизвольные процессы в гетерогенных системах (поверхностные явления) ΔGs < 0 (рисунок 5.6.1):
Рисунок 5.6.1 – Самопроизвольные процессы в гетерогенных системах
1. Поверхностное натяжение – состояние молекул или атомов, находящихся в поверхностном слое, иное, чем у молекул или атомов, находящихся в объеме фазы (рисунок 5.6.2).

986
Рисунок 5.6.2 – Поверхностное натяжение
Поверхностное натяжение (σ) – избыток энергии частиц в поверхностном слое на единицу площади поверхности [Дж/м2 =Н/м].
Поверхностное натяжение (σ) – это работа, которую требуется совершить для образования единицы поверхности.
Силовое определение поверхностного натяжения: σ – это сила, действующая на поверхности по касальной к ней и стремящаяся сократить поверхность тела [Н/м].
Поверхностное натяжение зависит от природы и агрегатного состояния контактирующих фаз (таблица 5.6.5).
Таблица 5.6.5 – Поверхностное натяжение некоторых жидких веществ на границе с воздухом при температуре 293 К
Зависимость поверхностного натяжения от температуры. При повышении температуры силы межмолекулярных взаимодействий ослабевают и поверхностное натяжение уменьшается.
Зависимость поверхностного натяжения от введения различных веществ (на примере водных растворов ПАВ и ПИВ).
ПАВ (поверхностно-активные вещества) – вещества, понижающие поверхностное натяжение водных растворов. Это органические соединения, обладающие дифильной природой – их молекулы одновременно содержат

987
неполярные гидрофобные участки (слабо взаимодействующие с молекулами воды) и полярные гидрофильные группы (сильно взаимодействующие с молекулами воды).
Неионогенные ПАВ – спирты, альдегиды, кетоны, сложные эфиры. Ионогенные ПАВ – органические кислоты, амины и их соли.
Изотермы ПАВ, отличающихся разной длиной углеродной цепи представлены на рисунке 5.6.3.
Рисунок 5.6.3 – Изотермы ПАВ, отличающихся разной длиной углеродной цепи
Молекулы ПАВ накапливаются на поверхности раздела фаз, понижая поверхностное натяжение.
Образование "частокола Ленгмюра" из молекул ПАВ на границе раздела раствор-воздух представлено на рисунке 5.6.4.
Рисунок 5.6.4 – Частокол Ленгмюра
ПИВ (поверхностно-инактивные вещества) – вещества,
повышающие поверхностное натяжение водных растворов (при больших концентрациях). Сильные неорганические электролиты – соли, кислоты, щелочи.

988
Ионы ПИВ сильно взаимодействуют с молекулами воды и стремятся уйти с поверхности вглубь жидкости. Появление их на поверхности повышает поверхностное натяжение.
ПНВ (поверхностно-неактивные вещества) – вещества, не изменяющие поверхностное натяжение водных растворов. Многоатомные спирты, углеводы. Силы межмолекулярных взаимодействий молекул ПНВ с молекулами воды и молекул воды между собой приблизительно равны. ПНВ не изменяют поверхностное натяжение.
Концентрация молекул ПНВ в поверхностном слое и внутри жидкости одинакова.
Изотермы ПИВ и ПНВ представлены на рисунке 5.6.5.
Рисунок 5.6.5 – Изотермы ПИВ и ПНВ
2. Адсорбция – процесс самопроизвольного перераспределения вещества между поверхностным слоем и объемом фазы. Основные понятия:
Адсорбент – фаза, на поверхности которой происходит адсорбция. Адсорбат или адсорбтив – вещество, которое адсорбируется на
поверхности.
Десорбция – процесс обратный адсорбции.
Сорбция – поглощение твердым телом или жидкостью вещества из окружающей среды.
Правило выравнивания полярностей (П. А. Ребинде ): Вещество может адсорбироваться на поверхности раздела фаз, если его присутствие в межфазном слое уравнивает разность полярностей этих фаз в зоне их контакта.
Типы адсорбции (рисунок 5.6.6):
Н – теплота адсорбции (мера интенсивности взаимодействия адсорбата с поверхностью адсорбента).
Рисунок 5.6.5 – Типы адсорбции

989
При адсорбции происходит самопроизвольное снижение удельной свободной поверхностной энергии (поверхностного натяжения).
Количественные характеристики адсорбции:
Избыточная гиббсовская адсорбция (Г) – избыток адсорбата в поверхностном слое по сравнению с его количеством в объеме фазы, отнесенный к единице площади поверхности (моль/м2), характеризует адсорбцию на жидкой поверхности.
Абсолютная адсорбция (ɑ) – количество адсорбата на единице массы адсорбента (моль/г), используется для характеристики адсорбции на твердой поверхности.
А) Адсорбция на границе жидкость (раствор) – газ (гиббсовская адсорбция). Фундаментальное уравнение адсорбции Гиббса (формула 5.6.5):
(5.6.5)
где с – концентрация вещества в растворе, R – универсальная газовая постоянная, T – абсолютная температура.
Размерность [Г] = [моль/ед. пл-ди поверхности], например, [моль/м2]. а) Если  < 0 , то Г > 0 — вещество накапливается в поверхностном
< 0 , то Г > 0 — вещество накапливается в поверхностном
слое (ПАВ); б) Если  > 0, то Г < 0 – вещество уходит в объем раствора (ПИВ);
> 0, то Г < 0 – вещество уходит в объем раствора (ПИВ);
в) Для ПНВ Г = 0.
Поверхностная активность (только для ПАВ) (формула 5.6.6):
(5.6.6)
Характеризует способность ПАВ накапливаться в поверхностном слое, снижая поверхностное натяжение.
Размерность [ g ] = [Дж · м · моль–1] = [Н·м2·моль–1].
Изотерма гиббсовской адсорбции и графическое определение поверхностной активности представлены на рисунке 5.6.7
Рисунок 5.6.7 – Изотерма гиббсовской адсорбции и графическое определение поверхностной активности

990
Правило Дюкло-Траубе – поверхностная активность ПАВ одного и того же гомологического ряда в водном растворе возрастает в среднем в 3,2 раза при увеличении цепи на одну группу -СН2-(рисунок 5.6.8).
Рисунок 5.6.8 – Изотермы адсорбции карбоновых кислот, отличающихся длиной углеводородного радикала
Б) Адсорбция на твердом теле:
-Физическая – взаимодействие адсорбента и адсорбата за счет сил Ван- дер-Ваальса и водородных связей (малоспецифична).
-Химическая (хемосорбция) – взаимодействие адсорбента и адсорбата за счет образования химических связей (строго специфична).
Примеры:
-физическая адсорбция: адсорбция аммиака на угле;
-химическая адсорбция: адсорбция углекислого газа на извести. Типичная изотерма мономолекулярной адсорбции на твердой
поверхности (рисунок 5.6.9):
Размерность [ɑ ] = [моль/единица массы адсорбента].
Рисунок 5.6.9 – Изотерма мономолекулярной адсорбции на твердой поверхности
Уравнение изотермы Ленгмюра (формула 5.6.7):
(5.6.7)
где ɑ∞ – величина предельной адсорбции, когда вся поверхность адсорбента заполнена адсорбатом, постоянна для всего гомологического ряда адсорбатов; к – постоянная для данного вещества, численно равная

991
равновесной концентрации адсорбата при адсорбции, равной половине предельной; сравн – равновесная концентрация адсорбата в фазе над адсорбентом.
Для экспериментального определения величины адсорбции на поверхности твердого тела используется уравнение (5.6.8):
(5.6.8)
где с0 – исходная концентрация вещества; сравн – равновесная концентрация, установившаяся после определенного по времени контакта адсорбента с раствором (газовой смесью); V – объем раствора (газовой смеси); m – масса адсорбента.
Размерность [ɑ] = [моль/кг].
Виды адсорбции на поверхности твердого тела, граничащего с жидкостью:
Молекулярная адсорбция – характерна для неэлектролитов. Ионная адсорбция – характерна для электролитов:
–эквивалентная – оба иона адсорбируются в эквивалентных количествах (слабые электролиты);
–обменная адсорбция – адсорбция одного из ионов электролита сопровождается одновременным вытеснением с адсорбента эквивалентного количества другого иона того же знака (сильные электролиты);
–избирательная адсорбция – на адсорбенте адсорбируются преимущественно ионы одного типа (сильные электролиты).
Применение адсорбции представлено на рисуноке 5.6.10:
Рисунок 5.6.10 – Применение адсорбции
Значение ПАВ представлено на рисунке 5.6.11.

992
Рисунок 5.6.11 – Значение ПАВ
5.6.3 Адгезия и когезия
Поверхностное натяжение различных конденсированных тел на границе с газом непосредственно связано с межатомным и межмолекулярным взаимодействием в конденсированной фазе. При анализе межфазовых взаимодействий часто используют понятия адгезии и когезии Взаимодействие (сцепление) молекул, атомов, ионов внутри одной фазы (гомогенной части системы) называют когезией. Когезия обусловлена теми же силами притяжения различной природы и определяет существование веществ в конденсированном состоянии. Когезионные силы иногда называют силами аттракции (притяжения).
Работу когезии Wk определяют как работу разрыва однородной гомогенной фазы с образованием двух новых поверхностей раздела этой фазы с ее собственным паром:
Если фазы а и б идентичны, то работа разрыва столбика единичного сечения соответствует работе когезии,
Если фазы а и б разные, то – работе адгезии.
В простейшем случае Wk равна обратимой работе разрыва столбика жидкости с единичной площадью сечения (формула 5.6.9):
993 |
|
Wk = 2 жп |
(5.6.9) |
Множитель 2 – образование двух новых одинаковых по величине и свойствам поверхностей раздела.
Применительно к идеальному твердому телу (отсутствие дефектов структуры) величину WK часто называют прочностью на разрыв
(обратимый), или когезионной прочностью.
Реальные тела из-за наличия дефектов структуры имеют значительно меньшую (иногда в 100-1000 раз) прочность.
Когезия отражает межмолекулярное взаимодействие внутри гомогенной фазы, поэтому ее могут характеризовать также такие параметры, как:
- энергия кристаллической решетки Ек.р.,
-внутреннее давление Рвн.,
-энергия парообразования Нп, -температура кипения Ткип,
-летучесть (определяемая равновесным давлением пара над телом) и
др.
Эти же параметры количественно характеризуют и поверхностное натяжение тел на границе с газом.
Точную информацию о когезии и поверхностном натяжении можно получить из термодинамических характеристик тел, связанных с энергией парообразования.
В процессе испарения вещества происходит полный разрыв межмолекулярных связей, поэтому работа когезии определяется энтальпией
парообразования (формула 5.6.10): |
|
Нп = ΔGп + T ΔSп |
(5.6.10) |
где ΔGп – изменение энергии Гиббса при парообразовании; ΔSп – изменение энтропии при парообразовании.
Энтальпия парообразования твердых тел равна энергии кристаллической решетки. В условиях равновесия между конденсированной и паровой фазами при p = const и T = const ΔGп = 0 и тогда получим выражение (5.6.11):
Нп = T ΔSп |
(5.6.11) |
Отсюда следует, что чем больше энтальпия парообразования, т. е. больше работа когезии, а значит и поверхностное натяжение, тем больше его энтропия (формула 5.6.12):
ΔSп = ΔS0 – R ln (p/pатм) |
(5.6.12) |
994
где ΔS0 – изменение энтропии парообразования при температуре кипения;
pатм – давление пара, равное атмосферному давлению
то чем больше работа когезии (больше поверхностное натяжение), тем меньше давление насыщенного пара над веществом при данной температуре (меньше летучесть).
При кипении p/pатм =1, тогда уравнение Нп = T ΔSп принимает вид
(5.6.13):
L = Tкип ΔS0 или L / Tкип = ΔS0 |
(5.6.13) |
где L – энтальпия парообразования при температуре кипения Tкип Величина S0 отнесенная к 1 моль вещества, имеет приблизительно
одинаковое значение для многих неассоциированных жидкостей (правило Трутона), равное 85–90 кДж/моль*К (формула 5.6.14):
Н/T = 88 кДж/моль*К |
(5.6.14) |
Когезию таких жидкостей (и поверхностное натяжение) можно оценивать и сравнивать по температуре кипения и энтальпии (теплоте) парообразования при температуре кипения.
Для жидкостей и большинства твердых тел когезионные силы выражаются в межмолекулярном взаимодействии, обусловленном ван-дер- ваальсовыми и водородными связями.
При разрушении твердых тел, имеющих атомную кристаллическую решетку (кристаллы углерода, германия, кремния и др.), разрываются ковалентные связи. Реакционная способность атомов на поверхности таких тел чрезвычайно велика. В условиях вакуума они способны образовывать между собой двойные связи, а на воздухе чаще всего реагируют с кислородом, образуя на поверхности оксидные пленки.
У ионных кристаллов распределение электрического заряда на поверхности значительно отличается от его распределения в объеме. В результате реакционная способность поверхности повышена к ионам противоположного заряда.
Разные кристаллические структуры резко отличаются по свойствам, в том числе и по энергии когезионных связей.
Прослеживается уменьшение этой энергии в ряду кристаллов:
ковалентные > ионные > металлические > молекулярные (В-д-В)
Кроме того, химическая и кристаллографическая структура различных граней одного и того же кристалла может существенно различаться. Более плотная упаковка атомов отвечает меньшей поверхностной энергии Гиббса данной грани и соответственно меньшей ее реакционной способности.

995
Работа адгезии Wa – как работа разрыва межфазного поверхностного слоя. В этом случае энергия затрачивается на образование двух поверхностей раздела, равных по величине, но разных по свойствам.
В системе ж/т работа адгезии (формула 5.6.15):
Wa = жп + тп - тж – уравнение Дюпре |
(5.6.15) |
Подставив в уравнение Дюпре два уравнения
(Wk = 2 жп и тп = тж + жпCos θ )
Получим:
Wa /Wk = 0.5 ( 1 + Cos θ )
или
Cos θ = 2 Wa /Wk – 1 = Wa / жп – 1
Wa /Wk = 0.5 (1 + Cos θ )
Cos θ = 2 Wa /Wk – 1 = Wa / жп – 1
Из уравнений следует:
При равенстве работ когезии и адгезии контактный угол θ=00, а
условие Wa/Wk > 1.0 приводит к неограниченному растеканию (это же условие является необходимым условием последующего растворения).
Движущую силу растекания определяют, как разницу работ адгезии и когезии и называют работой растекания. Количественно растекание характеризуется коэффициентом растекания ψ (формула 5.6.16):
 (5.6.16)
(5.6.16)
Величина адгезии всегда больше нуля, т.к. между соприкасающимися фазами всегда имеется какое-либо, пусть очень небольшое межмолекулярное взаимодействие.
Поэтому ситуация, когда Wa=0 и угол θ =1800, не возможна. Во всех известных экспериментально исследованных системах ж/т/п значения
996
краевого угла θ не превышали 1500 (в результате отношение работ адгезии и когезии всегда превышает величину ~0.07 ).
Три основных вида адгезии:
1.Физическая: между соприкасаемыми поверхностями образуется электромагнитная связь (пример – магнит или прилипание статически заряженных материалов)
2.Химическая: связь веществ на атомном уровне (паяние и сварка)
3.Механическая: самая простая адгезия путем прилипания адгезива к субстрату (происходит проникновение в поры верхнего слоя и сцепление с шероховатой поверхностью). Пример – окрашивание различных поверхностей.
Применение адгезии в различных отраслях:
1.Строительство: лакокрасочные материалы – качество прилипания и дальнейшее удержание. Гипсовые и цементно-песчаные смеси.
2.Металлургическое производство: важна адгезия специальных антикоррозионных и упрочняющих покрытий, красок, к тому же нужна плохая адгезия с водой
3.Механика: адгезия масла с элементами механизмов
4.Медицина: в стоматологии адгезия пломбы и зуба для качественной защиты и герметизации.
Адгезия между твердыми телами. Важно для теории прочности.
Синоним слова адгезия – прилипание Прилипание – процесс, а адгезия – результат
Площадь адгезионного контакта двух твердых тел определяется как их формой, так и микрошероховатостью поверхности.
5.6.4 Электрические свойства дисперсных систем
Характерны для систем, в которых на границе раздела фаз имеется двойной электрический слой (ДЭС).
При воздействии постоянного электрического тока на дисперсную систему можно наблюдать перемещение дисперсной фазы (Д.ф.) и дисперсионной среды (Д.с.) относительно друг друга.
В 1807г. Ф.Ф.Рейсс. (профессор Московского университета) проводил такой опыт: в сырую глину помещались две стеклянные трубки, в которые наливалась вода и опускались электроды (рисунок 5.6.12).

997
Рисунок 5.6.12 – Опыт Рейсса
При пропускании постоянного тока в анодном пространстве вода становилась мутной (частицы глины передвигались к положительному электроду), а в катодной трубке вода оставалась прозрачной, но уровень ей повышался.
Направленное движение частиц дисперсной фазы под действием электрического поля называется электрофорезом.
Движение дисперсионной среды в постоянном электрическом поле называется электроосмосом.
При наличии неподвижной капиллярно-пористой перегородки (в опыте Рейсса – это влажная глина) под действием постоянного электрического поля передвигаются дисперсионная среда (электроосмос) и дисперсная фаза (электрофорез).
В 1859 г. немецкий ученый Квинке обнаружил, что при течении воды под давлением через пористые материалы – М (глина, песок, графит и др.) возникает разность потенциалов – потенциал протекания (рисунок 5.6.13).
Рисунок 5.6.13 – Схема установки для наблюдения за потенциалом протекания
В 1878 г. Дорн установил, что при оседании частиц песка в сосуде с водой гальванометр (Г) фиксирует наличие тока (рисунок 5.6.14). Это явление, обратное электрофорезу, получило название потенциал
седиментации.

998
Рисунок 5.6.14 –Схема прибора Дорна
Эти явления получили название электрокинетических явлений. Причина электрокинетических явлений – наличие двойного
электрического слоя (ДЭС) на границе раздела дисперсной фазы и дисперсионной среды.
Механизм образования ДЭС у коллоидных частиц. ДЭС на границе раздела фаз возникает двумя основными путями:
1. За счет избирательной адсорбции.
При этом возможны два случая:
а) Избирательная адсорбция ионов, которые способны достраивать кристаллическуюрешетку частиц дисперсной фазы в соответствии с правилом Панета-Фаянса: кристаллическую решетку ядра достраивает тот ион, который находится в растворе в избытке и содержится в агрегате или родственен ему.
б) Избирательная адсорбция без достройки кристаллической решетки. Примером может служить образование ДЭС на частицах парафина, диспергированного в разбавленном водном растворе КОН. ДЭС образуется за счет избирательной адсорбции гидроксильных ионов, которые обладают большей адсорбционной способностью, чем ионы щелочного металла
(рисунок 5.6.15):
Рисунок 5.6.15 – Образование ДЭС на частицах парафина
2. За счет ионизации поверхности кристалла твердой частицы.

999
Таким путем возникает ДЭС на частицах водного золя SiО2. Поверхность кристаллов оксида SiО2 частично гидратируется.
Образуется H2SiО3, способная ионизироваться:
H2SiО3 ↔ H+ + HSiО3-
Ионы HSiО3-, «родственные» SiО2, избирательно адсорбируются на поверхности SiО2, придавая ей отрицательный заряд, а ионы водорода переходят в раствор (рисунок 5.6.16).
Рисцунок 5.6.16 – ДЭС на поверхности частиц SiО2
Строение двойного электрического слоя. Потенциалы ДЭС ДЭС состоит из потенциалопределяющих ионов (ПОИ), прочно
связанных с поверхностью дисперсной фазы, и эквивалентного количества противоположно заряженных ионов (ПРИ), находящихся в дисперсионной среде.
Между Д.Ф. и Д.С. возникает разность потенциалов – межфазный или
электротермодинамический потенциал (φ).
-ПРИ имеют конечные размеры, поэтому не могут подходить к твердой дисперсной фазе ближе, чем на расстояние радиуса одного иона.
-Слой ПРИ, которые компенсируют заряд твердой поверхности, состоит из двух частей: адсорбционного слоя и диффузного слоя.
-Адсорбционный слой ПРИ плотно прилегает к заряженной поверхности твердой частицы и имеет толщину, равную примерно диаметру гидратированного противоиона.
ПРИ адсорбционного слоя прочно связаны с заряженной твердой частицей адсорбционными и электростатическими силами.
ПРИ диффузного слоя притягиваются к заряженной частице только за счет электростатических сил, поэтому отрываются от неё при движении.
На границе скольжения между адсорбционной и диффузной частями
ДЭС коллоидной частицы возникает электрокинетический – дзета (ξ)
потенциал.
Образование ДЭС коллоидной частицы AgJ при взаимодействии разбавленных водных растворов AgNO3 и KI, взятого в избытке, (ионы которого J- и К+ выполняют роль стабилизатора).

1000
По правилу Панета-Фаянса на твердой фазе (кристаллах AgJ) будут адсорбироваться «родственные ионы» – J-. Это (ПОИ). Они образуют внутреннюю обкладку ДЭС и создают отрицательный по знаку, а по величине – электротермодинамический потенциал (φ).
Ионы К+ – (ПРИ) образуют внешнюю часть ДЭС. Часть ПРИ К+ располагаются близко от твердой поверхности AgJ и составляют с ПОИ
плотный адсорбционный слой.
Остальные ПРИ К+ под влиянием теплового движения образуют
диффузную часть ДЭС.
В адсорбционном слое электротермодинамический потенциал (φ)
падает линейно, в диффузном слое постепенно.
ДЭС отрицательно заряженной частицыAgJ (рисунок 5.6.17):
Рисунок 5.6.17 Двойной электрический слой:
а) – распределение зарядов; б) – падение электротермодинамического потенциала.
Строение мицелл лиофобных коллоидных растворов. Структурной единицей лиофобных коллоидов является мицелла (рисунок 5.6.18).
Мицелла состоит из электронейтрального агрегата и ионогенной
части.
Агрегат состоит из некоторого числа m молекул малорастворимого вещества дисперсной фазы.
Ионогенная часть – это адсорбционный и диффузный слои ДЭС.

1001
Рисунок 5.6.18 – Строение мицеллы: 1 – агрегат; 2 – ядро; 3 – адсорбционный слой; 4 – гранула; 5 – диффузионный слой; 6 – мицелла
Рассмотрим строение мицеллы коллоидного раствора AgJ (стабилизатор KJ).
Агрегат – это m[AgJ].
Агрегат m[AgJ] вместе с ПОИ (ионы J – в количестве n ионов) составляют ядро мицеллы, её твердую фазу, схематично представляемую так:
Часть противоионов – (n – х) катионов К+, вместе с ядром составляют
гранулу:
Знак заряда гранулы определяют ПОИ. Заряд гранулы равен сумме зарядов ПОИ и ПРИ адсорбционного слоя.
Гранула с окружающим её диффузным слоем (х катионов К+, необходимых для компенсации заряда ПОИ) образуют мицеллу.
В отличие от гранулы заряд мицеллы равен нулю.

1002
1)φ - электротермодинамический – φ ~ 1 В.
2)ζ (дзетта) - электрокинетический – ζ = 0,1 В

1003
Вмицелле с ионным стабилизатором, твердую фазу составляет агрегат
сПОИ, а все ПРИ находятся в жидкой фазе.
Вэлектрическом поле по этой условной границе происходит взаимное перемещение Д.Ф. (гранулы) и Д.С. (ПРИ диффузного слоя) к
противоположно заряженным электродам.
Влияние электролитов на величину ξ- потенциала. ζ - потенциал зависит от:
- толщины диффузного слоя и является мерой устойчивости коллоидных систем.
При сжатии диффузного слоя из-за увеличения концентрации электролитов в Д.С., часть противоионов переходит за границу скольжения в адсорбционный слой. (ζ - потенциал ↓).
Многозарядные ионы понижают величину ξ - потенциала больше однозарядных и могут вызвать перезарядку (изменить знак заряда коллоидных частиц).
При равенстве заряда больше понижают величину ζ - потенциала ионы с большим радиусом:
1. Введение в коллоидный раствор индифферентного электролита (ионы такого электролита не способны достроить кристаллическую решетку частицы дисперсной фазы).
При этом возможны два случая:
а) Электролит имеет один ион, одинаковый с ПРИ ДЭС золя. (К золю AgJ, стабилизированному KJ, добавлен KNО3.)
Это приведет:
-к увеличению общего числа ПРИ (К+)
-возрастет их содержание в адсорбционном слое (для компенсации заряда ПОИ),
-к уменьшению количества ПРИ в диффузном слое,
-ξ – потенциал ↓.

1004
б) Электролит не содержит ионов, входящих в ДЭС золя (к золю AgJ добавили FeCl3.)
-Fe3+, заряд которого одинаков по знаку с зарядом ПРИ, выступает в роли иона - конкурента за нахождение в ДЭС.
-Происходит ионный обмен, ξ - потенциал ↓
-Перезарядка коллоидной частицы, поскольку адсорбционная способность Fe3+>, т.к. > заряд.
2. Добавление к золю неиндифферентного электролита (один из ионов электролита может достраивать кристаллическую решетку частицы дисперсной фазы).
Возможны два случая:
К золю добавлен тот же электролит, который образовал его ДЭС.
а) к золю AgJ с отрицательным зарядом частиц, добавлен KJ. При небольших концентрациях такого электролита ζ - потенциал будет возрастать, а при больших концентрациях – уменьшаться, т.к. увеличение концентрации противоионов К+ будет приводить к уменьшениютолщины диффузногослоя.
б) к золю AgJ, стабилизированному KJ, добавлен AgNO3. Это приведет
ктому, что ионы Ag+, способные достроить кристаллическую решетку AgJ, образуют с ПОИ золя (J-) малорастворимое соединение, что приведет к постепенному снижении величины ζ - потенциала до нуля. Дальнейшее увеличение концентрации AgNО3 может привести к тому, что ионы Ag+ сообщат положительный знак заряда электронейтральной поверхности AgJ (произойдет перезарядка твердой поверхности).
Величину ζ - потенциала определяют по скорости электрофореза (V) (формула 5.6.17):
(5.6.17) (уравнение Гельмгольца-Смолуховского)
где:
ε – относительная диэлектрическая проницаемость среды; ε0 – электрическая постоянная, равна 8,9∙10-12 Ф/м; Е – ЭДС, В;
К – коэффициент, значение которого зависит от формы частиц; (для сферических К=6, для цилиндрических К=4) η| – вязкость среды, Н∙с/м2; ℓ – расстояние между электродами, м.
Скорость электрофореза при Е = 1 В/см называется
электрофоретической подвижностью. Эта величина строго постоянная для каждого вещества, поэтому используется в качественном анализе (антибиотиков, витаминов и др.).

1005
Скорости перемещения дисперсионной среды в электрическом поле
(скорости электроосмоса) (формула 5.6.18):
(5.6.18)
где:
χ – удельная электрическая проводимость золя; J – сила тока;
υ – объемная скорость, т.е. объем жидкости, перенесенной через пористую мембрану за единицу времени.
В медико-биологических исследованиях широко используется электрофоретический анализ белков сыворотки крови с целью диагноза заболеваний.
С помощью электрофореза в организм вводят различные лекарственные вещества и определяют чистоту лекарственных препаратов.
Электроосмос используется при обезвоживании перевязочных материалов, фильтров, для концентрирования растворов.
5.6.5 Получение дисперсных систем и их устойчивость
Устойчивость дисперсных систем – это способность дисперсной фазы сохранять во времени постоянство дисперсности частиц и состояние равномерного распределения их во всем объеме дисперсионной среды.
В дисперсных системах различают седиментационную (кинетическую) и агрегативную устойчивость.
Седиментационная устойчивость – это устойчивость к оседанию
дисперсной фазы под действиемсилы тяжести.
Факторами этой устойчивости являются:
-размер частиц,
-способность участвовать в броуновском движении;
-вязкость дисперсионной среды, (обуславливают энтропийный фактор устойчивости.)
Агрегативная устойчивость – это устойчивость частиц дисперсной фазы к агрегации – объединению частиц в более крупные агрегаты, т.е. способность сохранять неизменными свои размеры.
Агрегативнуюустойчивость обеспечивают два основных фактора:
электростатический и адсорбционно-сольватный.
Электростатический фактор защиты обусловлен наличием ДЭС на поверхности частиц дисперсной фазы и определяется величиной ζ – потенциала (создает электростатические силы отталкивания).
Адсорбционно-сольватный барьер защиты определяется наличием на поверхности противоинов диффузного слоя гидратных оболочек ориентированных диполей воды с большой плотностью (ρ), вязкостью (η) и упругостью.

1006
Это приводит к возникновению в тонких жидких пленках, разделяющих 2 твердые поверхности одноименно заряженных коллоидных частиц, расклинивающего давления.
Расклинивающее давление зависит от:
-заряда твердой фазы (φ потенциала),
-толщиныдиффузного слоя (ξ - потенциала).
Чем ↑заряд твердой фазы, чем ↑толщина диффузного слоя и ↑ ξ- потенциал, тем ↑ расклинивающее давление и ↑агрегативная устойчивость.
Агрегативную устойчивость с ионным стабилизатором рассматривают как результат взаимодействия двух противоположно направленных сил.
-вандерваальсовых сил межмолекулярного притяжения,
-электростатических сил отталкивания.
ξ– потенциал >30 мВ перекрытие и электростатическое отталкивание проявляются на расстояниях, при которых молекулярное притяжение слабое
иколлоидные частицы не агрегируют.
ξ– потенциал < 30 мВ при столкновении мицелл происходит перекрывание этих слоев, что приводит к преобладанию сил притяжения и потере агрегативной устойчивости.
Рисунок 5.6.19 – Схема агрегативной устойчивости мицелл коллоидных растворов
Коллоидные растворы с ионным стабилизатором:
-агрегативно неустойчивы, если их частицы имеют ξ < 30 мВ,
-относительно устойчивы, если 30 < ξ < 50 мВ,
-устойчивы при ξ > 50мВ.
Коагуляция – это процесс слипания коллоидных частиц из-за потери агрегативной устойчивости с образованиемболее крупных агрегатов.
Коагуляцию вызывают:
-концентрирование раствора,
-уменьшение и увеличение температуры,
-различные виды излучения,

1007
- добавление электролитов.
При коагуляции изменяются размеры и число частиц дисперсной фазы.
Коагуляция под действием электролитов. Для каждого электролита необходима своя минимальная концентрация – порог коагуляции (Ск).
Порог коагуляции – это минимальная концентрация электролита, которая вызывает явную коагуляцию коллоидного раствора (помутнение раствора или изменение его окраски) (формула 5.6.19).
(5.6.19)
где СК – порог коагуляции, моль/л; СО – молярная концентрация эквивалента исходного раствора электролита (коагулятора), моль экв/л,VЗ – и VK – объемы золя и электролита (мл), вызвавшего коагуляцию золь.
экв/л,VЗ – и VK – объемы золя и электролита (мл), вызвавшего коагуляцию золь.
Коагулирующая способность (γ) = 1/Ск Зависимость скорости коагуляции от концентрации электролита
представлена на рисунке 5.6.20
Рисунок 5.6.20 – Зависимость скорости коагуляции от концентрации электролита
Скрытая коагуляция – это стадия агрегации, при которой не наблюдается никаких внешних изменений золя, но в ультрамикроскопе можно наблюдать образование частиц. Точка S выражает одновременно порог коагуляции и критический потенциал, с которых начинается явная коагуляция.
Явная коагуляция – это такой процесс агрегации, при котором обнаруживаются видимые изменения; изменяется цвет раствора, появляется мутность и постепенно – осадок.
При медленной коагуляции скорость коагуляции резко возрастает с изменением концентрации электролита.

1008
Вобласти быстрой коагуляции увеличение концентрации электролита не изменяет скорость коагуляции (Vk=const).
На рисунке 5.6.20 OS (область I) – скрытая коагуляция; SK (область II)
–медленная коагуляция; KN (область III) – быстрая коагуляция; SN – явная коагуляция:
Минимальная концентрация электролита, при которой начинается быстрая коагуляция, называется порогом явной коагуляции (ск).
Величина ξ – потенциала, соответствующая ск – критическим ξ –
потенциалом или ξ кр.
В1882 году Шульце показал, что коагулирующей способностью
обладает один из ионов добавляемого электролита (ион-коагулятор). Коагулирующая способностью иона-коагулятора возрастает с увеличением его заряда. (правилоШульце).
В1900 году Гарди нашел, что заряд коагулирующего иона противоположен заряду коллоидной частицы (правило Гарди). Для золя с положительно заряженными частицами ионы-коагуляторы – анионы, для золя с отрицательно заряженными частицами – катионы.
Правило ШульцеГарди: Коагулирующим действием обладает тот ион электролита, который имеет заряд, противоположный заряду гранулы; коагулирующее действие тем сильнее, чем выше заряд иона-коагулятора (правило значности).
Правило Шульце-Гарди на основании опытных данных дает для 1-, 2- и 3-зарядных противоионов соотношение (рядШульце-Гарди) (формула
5.6.20):
(5.6.20)
Сk –пороги коагуляции областей I, II, III соответственно.
Позже было показано, что энергетический барьер между коллоидными частицами исчезает при достижении критической концентрации (Ск), которая обратно пропорциональна шестой степени заряда иона-коагулятора
(закон 6-й степени) (формула 5.6.21):
(5.6.21)
Т.о. для порогов коагуляции типично лиофобных золей имеем(формула
5.6.22):
(5.6.22)
Из правила Шульце-Гарди существуют исключения, обусловленные:
-химическим взаимодействием ионов с поверхностью;
-специфической адсорбцией многозарядных ионов.
1009
Особый случай – коагуляция под действием сложных органических ионов (алкалоиды, красители), проявляющих коагулирующее действие вне связи с валентностью. Часто органические ионы оказывают большее коагулирующее действие, чем ионы неорганических соединений.
Сильное влияние электролита на коагуляцию коллоидных растворов надо учитывать при введении растворов солей в живые организмы. Имеет значение не только концентрация вводимых ионов, но и их заряд.
Например, изотонический раствор NaCl нельзя заменить раствором MgSО4, поскольку в этой соли имеются ионы Mg2+ и SО42-, обладающие более высокой коагулирующей способностью, чем ионы Na+ и Сl-.
При инъекциях электролита надо вводить его медленно, чтобы не вызвать коагуляцию биологических коллоидных систем.
Влияние электролитов на φ- и ξ – потенциалы. Механизм коагуляции. При быстрой коагуляции коллоидных систем электролитами возможны два механизма:
1)концентрационная коагуляция, при которой потеря устойчивости коллоидов вызывается сжатием диффузной части ДЭС при постоянном φ- потенциале поверхности;
2)нейтрализационная коагуляция, происходящая в результате снижения поверхностного φ-потенциала, и, как следствие, ξ –потенциала частиц.
Тип коагуляции зависит от свойств коллоида и от характера прибавляемого электролита.
Концентрационная коагуляция. Наблюдается в золях с высоким φ-
потенциалом частиц при увеличении концентрации электролита. Осуществляется при действии индифферентных электролитов (их
добавление не изменяет величину φ-потенциала во внутренней обкладке ДЭС).
Одновременно наблюдается электростатический эффект сжатия ДЭС и уменьшение ξ –потенциала, что приводит к коагуляции.
Наблюдается две основные закономерности, обусловливающие величину ск:
1)Влияние заряда иона-коагулятора по правилу Шульце-Гарди;
2)Влияние размера иона-коагулятора.
Влияние размера иона-коагулятора индифферентного электролита.
Лиотропные ряды. Ионы щелочных металлов по их порогам коагуляции располагаются в следующий ряд:
Li+ > Na+ > K+ > Rb+ > Cs+
Наибольший порог коагуляции (наименьшая коагулирующая способность) характерен для Li+. Это объясняется тем, развитая гидратная оболочка увеличивает общий радиус иона и препятствует его вхождениюв адсорбционнный слой.

1010
Для ионов щелочноземельных металлов:
Ca2+ > Sr2+ > Ba2+ > Mg2+
Анионы также можно расположить в лиотропный ряд, но разница в их коагулирующей способности незначительна.
Зависимость ξ – потенциала и порогов коагуляции отрицательно заряженного золя от концентрации однозарядных катионов в лиотропном ряду представлена на рисунке 5.6.21.
Рисунок 5.6.21 – Зависимость ξ – потенциала и порогов коагуляции отрицательно заряженного золя от концентрации однозарядных катионов в лиотропном ряду
Нейтрализационная (адсорбционная) коагуляция:
-Происходит в результате уменьшения φ –потенциала.
-Вызывают электролиты, имеющие ион, способный к специфической адсорбции на поверхности частиц и заряженный противоположно, т.е.
неиндифферентные электролиты.
-Способность к адсорбции возрастает с увеличением заряда иона-
коагулятора.
-ионы, находясь в адсорбционном слое, нейтрализуют φ -потенциал и снижают его ξ – потенциал. Это может привести к перезарядке поверхности частиц, поэтому нейтрализационная коагуляция ограничена пределами
концентрации электролита.
Потерю агрегативной устойчивости золями при специфической адсорбции ионов-коагуляторов объясняют не только снижением электрических потенциалов частицы, но и образованием на поверхности частиц менее растворимых соединений.
При этом уменьшается взаимодействие частиц с растворителем и увеличивается поверхностное натяжение на границе частица - среда, что усиливает тенденциюк агрегации.

1011
Порог нейтрализационной коагуляции обратно пропорционален квадрату величины заряда z иона-коагулятора (формула 5.6.23):
(5.6.23)
При коагуляции смесями электролитов может наблюдаться (рисунок
5.6.22):
-аддитивное действие;
-антагонизм;
-синергизм.
Аддитивность – это суммирование коагулирующего действия ионов, вызывающих коагуляцию.
Антагонизм – это уменьшение коагулирующего действия одного электролита в присутствии другого.
Синергизм – это усиление коагулирующего действия каждого из ионов - коагуляторов в присутствии другого иона-коагулятора в смеси.
Рисунок 5.6.22 – Схема совместного действия 2-х электролитов на золь: 1 – аддитивность; 2- антагонизм;3- синергизм.
На осях: концентрации коагуляции = за 100%.
В случае аддитивности – (прямая 1) 1-го электролита -70%, то 2-го- 30%(100%).
При антагонизме (кривая 2) на 70% концентрации 1-го электролита нужно уже больше, например, 55%. Таким образом, сумма их концентраций станет больше 100%.
При синергизме (кривая 3) для 70% достаточно добавить, например, только 15% от концентрации коагуляции второго электролита (в сумме меньше 100%).
При введении в организм лекарственных веществ в виде инъекций они могут быть антагонистами, синергистами или проявлять аддитивность.
1012
Взаимная коагуляция – это коагуляция, которая наблюдается при смешивании двух коллоидных растворов с противоположнымзарядом гранул.
1. Частный случай электролитной коагуляции: один из золей - это электролит с огромным ионом-коагулятором.
-Положительно заряженная частица золя Fe(OH)3 по отношению к отрицательному золю As2S3 – ион-коагулятор, прибавление которого снижает величину ξ-потенциала. (Золь-коагулятор должен быть добавлен к коагулируемому золю в определенном количестве.)
2. Однако между обычной электролитной коагуляцией и взаимной коагуляцией имеется существенное различие:
-При определенном соотношении количеств смешиваемых золей при взаимной коагуляции всегда наступает перезарядка.
Чтобы вызвать полную коагуляцию, т.е. полное выпадение дисперсной фазы обоих золей, они должны быть взяты в количествах, обеспечивающих эквивалентность положительных и отрицательных зарядов, т.е. ξ-потенциал
=0.
При взаимной коагуляции золей Fe(OH)3 и As2S3 :
-в объемном соотношении 9:1 – коагуляция не наблюдается;
-при 7:3; 5:5 – частичное осаждение, но ссохранением положительного заряда частиц;
-При 3:7 – полное осаждение, ξ-потенциал = 0.
-При дальнейшем увеличении объема в пользу AS2S3 происходит перезарядка смеси с (+) на (-) и неполное выпадение осадка;
-при 1:100 коагуляция опять не обнаруживается.
Явление привыкания – это повышение устойчивости золя к коагулирующему действию электролита при уменьшении скорости его поступления.
Это наблюдается, если электролит добавлять к золю малыми порциями через большие интервалы времени. В этом случае Ск будет больше, чем при добавлении сразу большого количества электролита.
В организме это явление проявляется в привыкании к некоторым лекарствам, курению, наркотикам.
Чередование зон коагуляции. Рассмотрим зависимость ξ-потенциала
коллоидного раствора с отрицательным зарядом частиц от концентрации введенных электролитов (рисунок 5.6.23): KNО3, Ca(NО3)2, Al(NO3)3,
Th(NО3)4.

1013
Рисунок 5.6.23– Зависимость ξ-потенциала золя от концентрации введенных электролитов: 1 - KNО3, 2 - Ca(NО3)2, 3 - Al(NО3)3, 4 - Th(NО3)4; заштрихованная
область – неустойчивое состояние золя.
При добавлении К+ и Са2+ к золю (кривые 1 и 2) – постепенное понижение ξ – потенциала; при ξ1 кр. – золь коагулирует.
На них две зоны – устойчивого золя и коагуляции (заштрихованная область).
При добавлении А13+ и Th4+ (кривые 3 и 4) – 2 зоны стабильности и 2 зоны коагуляции.
üотрицательный ξ-потенциал постепенно понижается, доходит до критического значения (ξ1кр.).
-I зона коагуляции.
-Затем ξ -потенциал переходит через изоэлектрическую точку (ξ = 0).
-Отсутствие коагуляции (незаштрихованная область). При ↑ концентрации - перезарядка.
Образуется золь с положительным зарядом гранул и отмечается повышение положительного ξ -потенциала.
-Который достигает max, а потом понижается до второго критического значения (ξ2кр.). Золь при этом коагулирует уже под действием ионов NO3 -
(2-я зона коагуляции).
-Чередование состояний электронейтральности и заряженности частиц золя называют чередованием зон коагуляции.
Коагуляцию гидрофобных коллоидов вызывает огромное множество причин:
-резкие изменения температуры;
-механическое перемешивание;
-введение химических реагентов;
-воздействие электромагнитных полей;
-воздействие различных излучений и т.д.
Во всех случаях происходит воздействие на различные факторы
агрегативной устойчивости.

1014
Наиболее существенное влияние оказывает введение электролитов. Влияние электролита связывают с воздействием на структуру ДЭС.
Возникло много теорий, которые пытались объяснить три вопроса:
1)Почему коагуляция наступает при определенной концентрации электролита-коагулятора?
2)Почему при этом основную роль играет концентрация иона, несущего заряд, противоположный заряду частицы?
3)Почему влияние заряда иона-коагулятора подчиняется закономерности, выраженной правиломШульце-Гарди?
Все теории коагуляции можно подразделить на адсорбционные и
электростатические.
Адсорбционная теория коагуляции Фрейндлиха. Положения теории:
- ионы-коагуляторы адсорбируются коллоидными частицами в соответствии с изотермой адсорбции (формула 5.6.24):
(5.6.24)
-коагуляция наступает при одинаковом понижении ξ–потенциала, которое достигается при адсорбции эквивалентных количеств различных ионов.
-снижение ξ – потенциала до критического значения связано с уменьшением числа зарядов ПОИ из-за нейтрализации их адсорбирующимися ионами-коагуляторами.
-Позднее было показано, что теория имеет ограниченное применение, т.к. не всегда происходит эквивалентность адсорбции разных электролитов и совпадение изотерм адсорбции различных ионов.
-Коагуляция также может быть связана с изменениями лишь в диффузном слое, а заряд в слое ПОИ остается постоянным.
Электростатическая теория коагуляции Г. Мюллера. Положения теории:
-введение электролита в золь не изменяет общего заряда в ДЭС частицы, а вызывает сжатие диффузного слоя.
-это приводит к снижению ξ – потенциала, что и уменьшает стабильность золя.
Теория Мюллера не учитывала адсорбцию введенных ионов и их вхождение в структуру ДЭС.
Теория коагуляции Дерягина и Ландау, Фервея и Овербека (ДЛФО) (1937-1941г.). Положения теории ДЛФО:
-между любыми частицами при их сближении возникает расклинивающее давление разделяющей жидкой прослойки в результате действия сил притяжения и отталкивания.
-состояние системы зависит от баланса энергии притяжения и энергии отталкивания.

1015
-преобладание энергии отталкивания приводит к устойчивости систем, наблюдается положительное расклинивающее давление.
-преобладание энергии притяжения вызывает нарушение агрегативной устойчивости, т.е. коагуляцию за счет создания отрицательного
расклинивающего давления.
Составляющие расклинивающего давления имеют различную
природу:
а) электростатическую, обусловленную взаимным перекрыванием
ДЭС;
б) адсорбционную, связанную с адсорбцией молекул стабилизатора; в) структурную, возникающую при образовании граничных слоев
растворителя и обуславливающую создание адсорбционно-сольватного барьера в лиофильных системах;
г) молекулярную, обусловленную ван-дер-ваальсовыми силами притяжения.
Составляющие, а), б), в) вносят положительный вклад в расклинивающее давление, составляющая г) – отрицательное значение
Расклинивающее давление проявляется в энергии взаимодействия между частицами.
Даннуюзависимость можно представить графически (рисунок 5.6.24). На оси абсцисс откладывают расстояние между частицами (h). Энергию отталкивания (UОТТ.) принимают за положительную и
откладывают на оси ординат вверх от начала координат. Изменение этой энергии – кривая 1.
Энергию притяжения Uпр., как отрицательную, откладывают вниз от оси абсцисс.
Изменение энергии притяжения от расстояния – кривая 2.
Суммарную энергию системы из двух частиц получают сложением
UОТТ. и Uпр. :
Рисунок 5.6.24 – Потенциальные кривые взаимодействия двух частиц:

1016
1 - энергия отталкивания;
2 - энергия притяжения;
3 - результирующая кривая.
Суммарная энергия системы из двух частиц (формула 5.6.25):
(5.6.25)
где В – множитель, зависящий от значений электрических потенциалов ДЭС, свойств среды, температуры;
е – основание натурального логарифма; δ – толщина диффузного слоя;
h – расстояние между частицами частицами; А – константа молекулярных сил притяжения.
Слагаемые расклинивающего давления имеют разные знаки (UОТТ. > 0, Uпр < 0), и знак суммарного расклинивающего давления зависит от преобладания какого-то из взаимодействий.
Суммарное расклинивающее давление вычисляют алгебраическим сложением ординат кривых 1 и 2 на различных расстояниях h. Строят результирующую кривую потенциальной энергии системы – кривая 3.
Положения теории ДЛФО хорошо согласуются с поведением
гидрофобных золей и корректно объясняют влияние электролитов на коагуляцию.
а) Если частицы золя имеют высокий электрический потенциал и достаточной толщины диффузный слой (большой ξ – потенциал), то при перекрывании ДЭС двух частиц энергия электростатического отталкивания преобладает над энергией межмолекулярного притяжения.
Возникает энергетический барьер, препятствующий сближению частиц и они отдаляются друг от друга. Система является агрегативно устойчивой.
б) Сжатие диффузного слоя при добавлении электролитов, приводит к уменьшению ξ – потенциала, снижениюсил отталкивания.
в) При определенном значении ξ – потенциала и концентрации электролита – полное исчезновение потенциального барьера ( Uб.= 0).
Наблюдается быстрая коагуляция.
Подход по теории ДЛФО к устойчивости системы через энергетические кривые и расклинивающее давление - универсален. Дисперсная система агрегативно устойчива при высоком энергетическом барьере сил отталкивания. Факторы, снижающие Uб., понижают агрегативнуюустойчивость системы.
Коллоидная защита. Это повышение агрегативной устойчивости лиофобных золей при добавлении некоторых веществ.
Такими веществами являются ВМС (белки, полисахариды) и некоторые коллоидные ПАВ. Это проявляется в повышении значений

1017
порогов коагуляции у защищенного золя и неподчинению правилуШульцеГарди.
Если к золю Fe(OH)3 добавить небольшое количество раствора желатина, то для коагуляции такого золя потребуется намного больше электролита, чем для коагуляции незащищенного золя.
Способность защищать золи от коагуляции количественно выражают защитным числом. Это число мг сухого ВМС, которое защищает 10 мл данного золя от коагуляции его 1 мл 10% раствора NaCl.
В зависимости от природы золя защитное число называют «золотым», если оно относится к золю золота, «серебряным» - для золя серебра «железным» для оксида железа и т.д.
Чем больше защитное число, тем слабее защитное действие данного
ВМС.
Объясняется коллоидная защита адсорбцией защитных веществ на поверхности коллоидных частиц. Коллоидные ПАВ и ВМС ориентируются на поверхности коллоидных частиц: гидрофобными участками к частицам дисперсной фазы, а гидрофильными наружу, к воде.
Система при этом лиофилизируется, мицеллы приобретают дополнительный фактор агрегативной устойчивости за счет гидратных оболочек защищающих веществ (рисунок 5.6.25).
Рисунок 5.6.25 – Схема защитного действия макромолекул ВМС на частицы коллоидного раствора
Основными условиями защитного действия являются:
-хорошая растворимость ВМС в дисперсионной среде коллоидного раствора;
-хорошая адсорбируемость молекул ВМС на коллоидных частицах;
-достаточно большая концентрация ВМС, которая обеспечивает образование мономолекулярного адсорбционного слоя из макромолекул ВМС, полностью покрывающего всю поверхность мицелл золя.
Наибольшее защитное действие отмечается при одноименных зарядах ВМС и коллоидной частицы.

1018
Коллоидная защита играет большую роль в физиологических процессах. Так, содержание кальция карбоната и фосфата в крови значительно превышает их растворимость в воде. Отложению этих солей препятствуют защитные вещества крови, которые не позволяют коллоидным частицам объединяться в крупные агрегаты и осаждаться.
В медицинской практике применяют препараты защищенных коллоидов: протаргол, колларгол, ихтиол, которые содержат определенное количество серебра, к которому добавлен белок.
Существует теория, согласно которой гидрофильность белков и их способности к адсорбции на холестерине понижается с возрастом; как следствие, холестерин откладывается на стенках сосудов, вызывая в них возрастные изменения. Ослабление защитных свойств белков крови приводит к образованию камней в почках, печени, выпадение солей мочевой кислоты при подагре.
Пептизация – это процесс превращения осадка, образующегося в результате коагуляции, в устойчивый коллоидный раствор (процесс,
обратный коагуляции).
Различают 3 способа пептизации:
-адсорбционная пептизация;
-химическая (диссолюционная) пептизация;
-промывание осадка (коагулята) чистым растворителем (дисперсионной средой).
FeCl3 + 3NН3 ∙Н2О→Fe(OH)3↓ + 3NH4Cl
Перевести этот осадок в раствор (пептизировать) можно двумя путями: 1) Добавить к нему избыток раствора FeCl3 (пептизатор).
(адсорбционная пептизация.) «Родственные» ионы Fe3+ будут адсорбироваться на частицах осадка и сообщать им положительный заряд.
Частицы осадка в результате электростатического отталкивания одноименных зарядов будут переходить во взвешенное состояние - золь.
{m[Fe(OH)3] ∙ nFe3+∙ 3(n - х) Сl- }3x+ ∙ 3x Сl-
2) Добавить НСI. (диссолюционная химическая пептизация).
Пептизатор образуется в результате реакции:
Ионы FeO+ в соответствии с правилом Панета-Фаянса будут избирательно адсорбироваться на частицах осадка Fe(OH)3.
Мицелла образовавшегося золя в этом случае имеет такое строение:
{m[Fe(OH)3] ∙ nFeО+∙ (n - х)Сl- }x+ ∙ xСl-

1019
Процесс пептизации лежит в основе лечения:
-атеросклероза,
-«камней» в желче- и мочевыводящих путях;
-тромбов в кровеносных сосудах под действием антикоагулянтов.
-Коллоиды клеток и биологических жидкостей организма подвержены коагуляции.
-Образование тромбов в кровеносных сосудах, слипание эритроцитов представляют собой процессы, аналогичные коагуляции.
Одной из причин патологических изменений могут быть электролиты, поскольку коллоиды всех клеток организма находятся в постоянном контакте
сэлектролитами и малейшее изменение постоянства концентрации ионов или качественного состава их может привести к нарушению агрегативной устойчивости коллоидов - коагуляции.
-В организме имеют место: явление привыкания (к алкоголю, наркотикам и некоторым лекарственным препаратам);
-действие смеси электролитов или многокомпонентных лекарственных препаратов.
5.6.6 Молекулярно−кинетические и оптические свойства
дисперсных систем
Молекулярно-кинетические свойства коллоидных систем, как и
обычных растворов НМС, обнаруживаются в таких явлениях, как:
-броуновское движение,
-диффузия,
-осмос.
Броуновское движение – это хаотическое непрерывное движение частиц дисперсной фазы под действием ударов частиц дисперсионной среды, находящихся в молекулярно-тепловом движении.
Коллоидная частица, совершая зигзагообразно-поступательное движение, изменяет направление ~ 1014 раз за 1 с.
Среднее смещение за некоторое время τ вычисляют по уравнению А.Эйнштейна и М.Смолуховского (формула 5.6.26):
(5.6.26)
где Д – коэффициент диффузии.
Интенсивность броуновского движения изменяется в зависимости
от:
1)Температуры: чем ↑ t, тем ↑.
2)Вязкости дисперсионной среды: чем ↓ вязкость, тем ↑;
3)размеров частиц: чем ↓ размер, тем ↑ интенсивность броуновского движения.
Диффузия - это самопроизвольный процесс выравнивания концентрации частиц по всему объему раствора.
- Причиной диффузии, с позиций термодинамики, является стремление системы к максимальной энтропии.

1020
-Протекает под влиянием теплового (броуновского) движения.
-Процесс необратим.
-Диффузия прекращается, когда концентрация (и химический потенциал) частиц станет одинаковой по всему объему раствора.
I закон Фика.
Масса (m) вещества, продиффундировавшая за время τ из первого слоя
сконцентрацией c1 в другой слой, в котором концентрация его с2, при расстоянии между слоями х прямо пропорциональна площади поверхности S, через которую идет диффузия, промежутку времени τ, разности концентраций с, и обратно пропорциональна расстояниюмежду слоями
(формула 5.6.27):
(5.6.27)
где Д – коэффициент диффузии (коэффициент пропорциональности). Коэффициент диффузии численно равен массе вещества, которое
диффундирует в единицу времени через единицу площади при градиенте концентрации, равном 1 (физический смысл величины D).
Коэффициент диффузии сферических частиц определяют по уравнению Эйнштейна (формула 5.6.28):
(5.6.28)
где NА – число Авогадро;
R – универсальная газовая постоянная; Т – температура, К;
η – вязкость дисперсионной среды, Н∙с/м2; r – размер диффундирующей частицы, м.
Уравнение Энштейна является одним из основных в коллоидной химии для определения размеров коллоидных частиц и молекулярной массы полимеров по величине D.
Молекулярную массу вещества определяют по формуле 5.6.29:
(5.6.29)
где ρ – плотность вещества дисперсной фазы (полимера)
Осмос происходит при разделении двух растворов различной концентрации или раствора и чистого растворителя полупроницаемой мембраной.
Наблюдается движение растворителя из раствора с меньшей концентрацией в раствор с большей концентрацией.
Этот процесс в термодинамической трактовке обусловлен ростом энтропии системы, а в кинетической – избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора.

1021
Как и в истинных растворах, Росм. коллоидных растворов пропорционально концентрации их растворов (формула 5.6.30):
(5.6.30)
где Cv - частичная концентрация (число коллоидных частиц в единице объема).
Частичная концентрация определяется отношением массы дисперсной фазы mд.ф. в объеме Vpacтвopa к массе m коллоидной частицы (формула
5.6.31):
(5.6.31)
Коллоидные растворы имеют низкое Росм.
Например, Росм. 1% раствора золя золота при 20°С равно 0,045 кПа, Росм. 1% раствора сахарозы при тех же условиях составляет 72,5 кПа
(формула 5.6.32).
(5.6.32)
где r – размер коллоидных частиц.
↑ размера частиц в 2 раза - ↓ Росм. в 8 раз.
-Непостоянство величины Росм. во времени. Это объясняется агрегацией коллоидных частиц, в результате которой размер частиц возрастает, а суммарное число их - уменьшается.
-Молекулярно-кинетические свойства присущи не только истинным растворам, но и коллоидным.
Нет качественных различий в их молекулярно-кинетических свойствах. Различия только количественные, обусловленные различием размера частиц.
Седиментация - это процесс оседания частиц дисперсной фазы в
дисперсионной среде под действием силы тяжести.
На частицы дисперсной фазы в растворе действуют:
-сила тяжести;
-сила трения.
Сила тяжести по закону Архимеда (формула 5.6.33):
(5.6.33)
где Fm – сила тяжести, кг∙м/с2;
r – радиус частицы дисперсной фазы, м; ρ и ρ0 – плотность частиц д.ф. и д.с., кг/м3;

1022
g – ускорение силы тяжести (9,8 м/с2).
Сила трения (Fтр.), действующая на сферическуючастицу, согласно
закону Стокса:
Fтр = 6 ∙ π ∙ r ∙ η ∙ υ
где η – вязкость дисперсионной среды, Па∙с; υ – скорость движения частицы, м/с;
r – радиус частицы дисперсной фазы, м.
Если Fm = FТP, то седиментация частиц дисперсной фазы происходит с постоянной скоростью (формула 5.6.34):
|
(5.6.34) |
Способность к седиментации часто выражают через константу |
|
седиментации (Ксед) (формула 5.6.35): |
|
Ксед = υ/g |
(5.6.35) |
1/Ксед. – это мера кинетической устойчивости дисперсной
системы.
Седиментации противодействует диффузия, которая стремится выравнять концентрацию частиц дисперсной фазы по всему объему дисперсионной среды.
Состояние, при котором скорость диффузии равна скорости оседания,
называется седиментационно-диффузионным равновесием.
Если при установлении седиментационного равновесия основная масса частиц дисперсной фазы за небольшое время окажется в осадке, то систему
считают седиментационно-неустойчивой. |
|
||
Коллоидные |
растворы |
– |
седиментационно-относительно |
устойчивые.
Скорость седиментации коллоидных частиц сильно увеличивается,
если использовать центрифуги и ультрацентрифуги.
В ультрацентрифугах центробежная сила в сотни тысяч + млн. раз больше g.
Центральной частью центрифуги является ротор с частотой вращения
60000 об/мин. и выше.
Спомощью центрифугирования можно определять размер коллоидных частиц; разделять смесь белков, нуклеиновых кислот, полисахаридов и гормонов; выделять из растений и биосред организма биологически активные вещества.
Оптические свойства дисперсных систем. Свет, проходя через дисперснуюсистему, может:
- преломляться,

1023
-отражаться,
-поглощаться или рассеиваться.
Зависит это от соотношения между размером частиц дисперсной фазы и длиной волн (λ) падающего света (белый свет имеет длины волн (3,6 ÷7,6∙10-7 м).
В истинных растворах частицы растворенного вещества имеют размеры меньше, чем длины волн видимого света, поэтому они пропускают свет (оптически пусты) и являются прозрачными.
Грубодисперсные системы, размеры частиц в которых больше 10-6 м, т.е. значительно превышают λ видимого света, отражают свет и поэтому мутные.
Размер коллоидных частиц ≈ λ падающего света.
Поэтому для коллоидов характерно дифракционное рассеяние света. Световая волна изгибает коллоидную частицу. Свет рассеивается, и частица становится вторичным источником света. Рассеяние света можно наблюдать при боковом освещении коллоидного раствора: в случае точечного источника света – в виде светящегося конуса (эффект Фарадея-Тиндаля), а при обычном боковом освещении – в виде голубоватой опалесценции раствора. По конусу легко отличить коллоидные растворы от истинных
(рисунок 5.6.26).
Рисунок 5.6.26 – Эффект Фарадея-Тиндаля.
1)источник света;
2)коллоидный раствор;
3)направление наблюдения
Закон светорассеяния: (Рэлей) Интенсивность рассеянного света (J) прямо пропорциональна интенсивности падающего света (JO), частичной концентрации золя (СV), квадрату объема коллоидной частицы (V) и обратно пропорциональна длине волны падающего света (λ) в четвертой степени
(формула 5.6.36):
(5.6.36)
где К – константа.

1024
К зависит от соотношения показателей преломления дисперсной фазы (n1) и дисперсионной среды (n0) (формула 5.6.37):
(5.6.37)
Интенсивность рассеянного света тем больше, чем больше различаются показатели преломления коллоидной частицы и среды (при равенстве показателей преломления рассеяние света может отсутствовать).
Уравнение Рэлея справедливо при условиях:
-частицы имеют сферическую форму и не поглощают свет, т.е. бесцветны;
-коллоидный раствор является разбавленным (расстояние между частицами больше длин волн падающего света).
Из уравнения Рэлея видно:
-Чем ↓ λ, тем ↑ рассеяние. (Поэтому сильнее рассеиваются короткие волны (голубая часть спектра). Этим объясняется голубоватая окраска многих бесцветных золей при наблюдении сбоку и желтовато-красная - в проходящем свете.
Явление рассеяния света коллоидными частицами использовано в приборах ультрамикроскопах. У них pазрешающая способность, как в обычных микроскопах, но используется боковое освещение и темный фон. В результате дифракции света коллоидные частицы обнаруживаются в виде светящихся точек. Интенсивность рассеянного света зависит от концентрации золя, размеров и формы коллоидных частиц.
Ультрамикроскопию применяют при исследовании крови, лимфы, вакцин, для контроля чистоты инъекционных растворов, воды и воздушной среды, можно определить форму и размер коллоидных частиц.
Более точно о форме и размерах коллоидных частиц можно судить с помощью электронного микроскопа. В нем используются не лучи света, а поток электронов. Источником электронов служит вольфрамовая проволока, которая при накаливании испускает электроны. Стеклянные линзы заменены магнитными или электрическими полями. Микроскоп дает увеличение до 900 000 раз.
-Чем ↓ размер частиц, тем ↑ поглощаются короткие волны. Этим определяется различный цвет окрашенных золей (золота, рубина и др.).
-Белые золи не поглощают свет.
Определение формы и размеров коллоидных частиц.
Форму коллоидных частиц можно определить при помощи ультрамикроскопа. Если частицы ассиметричны, то они обладают переменной яркостью. Шарообразные частицы обладают постоянной яркостью.
Размеры коллоидных частиц можно определить:

1025
-по коэффициенту диффузии (по уравнению Эйнштейна);
-с помощью ультрамикроскопа: в определенном объеме (V) поля зрения микроскопа подсчитывают число частиц (n), равное числу светящихся точек.
-нефелометрически. Метод основан на сравнении светорассеяния стандартного коллоидного раствора (с известным радиусом частиц) и исследуемого золя той же массовой концентрации.
-ультрацентрифугированием;
Скорость седиментации частиц в ультрацентрифуге рассчитывают по уравнению (5.6.38):
(5.6.38)
заменив в нем g на w2x, где w – угловая скорость вращения ротора центрифуги;
х – расстояние от частицы до оси вращения.
- на молекулярных ситах – метод гельфильтрации.
5.6.7 Коллоидно-химические основы охраны природной среды
При рассмотрении проблем охраны атмосферы от загрязнений встречаем следующие коллоидно-химичесие процессы:
1)конденсационное формирование частиц твердой (дымы, аэрозоли) и жидкой дисперсной фазы (туманы, капли жидкости) и совместного формирования частиц, насыщенных жидкой фазой (смог);
2)агрегативную и кинетическую устойчивость аэродисперсных систем (осаждение облаков дисперсиями галогенидов серебра или твердой углекислоты, частые дожди в загрязненной атмосфере больших городов, очистка отходящих газов от твердых частиц методом нарушения устойчивости при электрокоагуляции);
3)диспергационные загрязнения атмосферы твердыми загрязнениями (пыльные бури, эрозия почвы);
4)коллоидные свойства твердых и жидких загрязнителей атмосферы – аэрозолей (диффузия, броуновское движение, светорассеяние в аэродисперсных системах, загрязняющих атмосферу); особая опасность коллоидно-дисперсных аэрозолей – взрывоопасность аэрозолей (муки, сахара, угля и др.); высокая кинетическая устойчивость аэрозоля ртути способствует длительному времени сохранения способности отравлять людей;
5)пылеподавление на угольных шахтах и предприятиях, перерабатывающих минеральное сырье – избирательное смачивание, регулируемое с помощью поверхностно-активных веществ;
6)снижение токсичности выхлопных газов – каталитическое дожигание загрязняющих остатков топлива на специальных катализаторах,
1026
процесс связанный с адсорбцией и кинетикой геторогенных процессов на специальных катализаторах;
7) образование окислов азота и серы при сжигании различных видов топлива приводит к возникновению кислотных дождей (для снижения вероятности образования таких осадков, оказывающих вредное влияние на биосферу, в первую очередь на растительный мир, проводят очистку отходящих газов от оксидов серы и азота сорбционными методами).
Большая проблема в общей системе охранных мероприятий – защита подземных вод от загрязнений, выбрасываемых промышленными предприятиями. Очень часто промышленные загрязнения из прохудившихся подземных или заглубленных резервуаров или трубопроводов поступают через фильтрующий слой почвы в подземные водоемы.
Проблема защиты окружающей среды от протечки из емкостей сточных вод и попадания их в подземные природные резервуары чистой пресной воды заставляет искать эффективные антифильтрационные материалы. Большой урон природе наносят также протечки из ирригационных и магистральных каналов, приводящие к заболачиванию и засолению почвы вблизи них.
На магистральных каналах чаще всего применяют монолитные и сборные железобетонные лотки, изготовленные заводским способом или выполненные путем пневмонанесения бетона непосредственно на русло каналов. Железобетонные защитные покрытия обычно укладывают в местах проведения каналов через грунты с высокой фильтрующей способностью. Толщина таких покрытий составляет от 8 до 20 см и зависит от условий работы каналов, поэтому стоимость этого вида защиты от фильтрации высока и не всегда оправдывает себя в связи с несовершенством гидроизоляции швов на стыках железобетонных конструкций. Через возникающие трещины фильтрация воды достигает значительных размеров, сводя на нет эффект от применения железобетонных защитных противофильтрационных покрытий.
Экономически целесообразны и технически легко выполнимы коллоидно-химические методы обработки грунтов и использование некоторых природных высокодисперсных глин, поверхностно-активных веществ и водорастворимых полимерных соединений для механической и физико-химической кольматации почвы в руслах каналов и в прудах, куда сбрасываются сточные воды. Под термином «кольматация» понимается такая обработка грунта, в результате которой происходит потеря фильтрующей способности при набухании глинистых частиц.
Тонкодисперсные частицы глинистых материалов способны проникать в поры между крупными частицами грунта, где возможна их коагуляция, в результате чего резко понижается водопроницаемость грунта. В поровом пространстве формируется внутригрунтовой противофильтрационный слой мощностью 20-30 см в песчаных грунтах и до 10 см - в суглинках. Такой способ кольматации позволяет снизить на 95-98% фильтрационные потери на
1027
гидротехнических земляных сооружениях - прудах, водоемах сельскохозяйственного и промышленного назначения. Способность гидрофильных частиц глин к набуханию при смачивании водой приводит к снижению эффективного пористого пространства между частицами и подавляет фильтрацию воды через почву, кольматированную таким способом.
Глобальная проблема - загрязнение водного бассейна (морей, океанов, озер и рек) нефтью и нефтепродуктами – стоит на одном из первых мест в негативном воздействии промышленной деятельности человека на гидросферу. Ежегодно в воду попадает несколько миллионов тонн нефти и продуктов её переработки. Это происходит в результате катастроф нефтеналивных судов, перевозящих нефть из районов нефтедобычи в районы потребления, при аварийных ситуациях на морских нефтепромыслах, при нарушении целостности нефтепроводов и при сливе балластных и промывочных вод танкерами.
Вероятность загрязнения водного бассейна постоянно растет в связи с развитием нефтепромыслов на шельфе и повышением грузоподъемности и скорости нефтеналивных судов.
Коллоидная химия позволяет решить две из возможных проблем глобального загрязнения водного бассейна нефтепродуктами.
Таким образом, даже при кратком рассмотрении экологических проблем гидросферы и охраны водного бассейна можно отметить их тесную связь с коллоидно-химическими процессами:
-седиментация осадков естественного происхождения (минеральных и органических взвесей) и искусственных (производственные загрязнения различной химической природы, весьма разнообразной формы и размеров); следовательно, надо знать закономерности седиментации;
-коагуляция и флокуляция частиц или капель дисперсной фазы с целью их укрупнения и облегчения седиментации (поскольку речь идет о коагуляции, то возникает связь с нарушением агрегативной и кинетической устойчивости дисперсных систем и необходимо знать теорию стабилизации и коагуляции);
-удаление растворенных веществ осуществляется методом адсорбции на различных адсорбентах или пузырьках воздуха (здесь проявляется связь с теорией адсорбции из растворов на твердых адсорбентах и на поверхности раствора с воздухом или с другой жидкостью, а также с теорией и практикой эмульгирования, пенообразования и пенной сепарации).
Структура почвы считается оптимальной, если в ней преобладают водопрочные частицы размером 0,25-10 мм у чернозема и 0,25-3 мм у подзолистых почв. В природных условиях чаще всего встречаются агрегаты тонкодисперсных частиц различной степени агрегирования и распределения по размерам. Это приводит к тому, что при высыхании грунтов агрегаты частиц распадаются на единичные частицы и при воздействии ветра происходит эрозия почвы. Орошаемое земледелие также имеет свои
1028
недостатки – излишняя вода, попадая на поля, может приводить к их заболачиванию. В связи с этим возникает проблема структурирования почвы и изменения фильтрационных свойств и эта проблема теснейшим образом связана с разделом коллоидной химии, называемым физико-химическая механика и реология дисперсных систем.
При рассмотрении проблем защиты литосферы можно отметить связь со следующими коллоидно-химическими процессами:
-образовании коагуляционной структуры в почвах с целью снижения содержания тонкодисперсной фракции (менее 0,05-0,1 мм); при этом проявляются все закономерности структурообразования в дисперсных системах;
-создании антифильтрационных дамб из структурированных солеустойчивых глинистых систем с добавками водорастворимых адсорбированных полимеров для предотвращения заболачивания почвы вдоль оросительных каналов и полей вблизи прудов-испарителей сточной воды;
-укреплении прочности структуры грунта при бурении скважин с целью предотвращения проникновения (фильтрации) воды из водоносных горизонтов в нефтеносные;
-снижении прочности структуры и накопления внутренних напряжений при наложении механических полей на пласты угля и пустой породы при подземных разработках полезных ископаемых.
1029
5.7 ВЫСОКОМОЛЕКУЛЯРНЫЕ СОЕДИНЕНИЯ И ИХ РАСТВОРЫ
ПЛАН
5.7.1 Строение и свойства высокомолекулярных соединений (ВМС).
5.7.1.1Понятие о растворах высокомолекулярных соединений (ВМС). Биополимеры.
5.7.1.2Сравнительная характеристика растворов высокомолекулярных соединений, истинных и коллоидных растворов.
5.7.1.3Краткая структура белка.
5.7.1.4Белки, как высокомолекулярные электролиты. Изоэлектрическая точка белка и методы ее определения.
5.7.1.5Устойчивость растворов высокомолекулярных соединений. Методы осаждения биополимеров: высаливание, коацервация и их биологическое значение.
5.7.1.6Вязкость растворов ВМС. Вязкость крови.
5.7.1.7Коллоидно-осмотическое давление в растворах ВМС. Мембранное равновесие Доннана.
5.7.1.8Набухание и растворение ВМС. Механизм набухания. Факторы, влияющие на набухание. Биологическое значение набухания.
5.7.1.9Застудневание растворов ВМС. Факторы, влияющие на застудневание. Тиксотропия. Синерезис. Биологическое значение этих процессов.
5.7.1.1 Понятие о растворах высокомолекулярных соединений (ВМС). Биополимеры
Высокомолекулярные соединения (ВМС) – это вещества с большой молекулярной массой порядка 104–106 а.е.м. Макромолекулы построены из большого числа повторяющихся звеньев.
ВМС (или полимеры) получаются в результате полимеризации или поликонденсации. Все полимеры делятся на природные (белки, нуклеиновые кислоты и др.), синтетические (нейлон, полиэтилен и др.) и искусственные, которые получаются в результате химической обработки природных полимеров (например, целлофан, нитроклетчатка и др.)
Синтетические полимеры находят широкое применение в медицине (аппарат «искусственная почка», плазма крови, эндопротезирование и много др.).
Биополимеры являются структурной основой всех живых организмов. К ним относятся, прежде всего нуклеиновые кислоты, белки и их производные: нуклепротеиды, гликопротеиды, липопротеиды и т.д., а ткже гликоген. Эти соединения являются основным строительным материалом для протоплазмы и ядерного вещества клеток и содержатся во многих биологических жидкостях.
1030
Нуклеиновые кислоты являются полимерами, содержащими от десятков до сотен тысяч нуклеотидов. Они являются важнейшим классом биополимеров, выполняя генетические функции и определяя весь ход развития живого организма.
Полисахариды (крахмал, гликоген и др.) являются полимерами глюкозы. Они выполняют структурную функцию и являются запасной формой питательных веществ.
Белки являются природными полимерами, которые образуются в результате реакции поликонденсации аминокислот. Значение белков, нуклеиновых кислот, полисахаридов и их производных чрезвычайно велико, оно подробно рассматривается в курсе биохимии.
5.7.1.2Сравнительная характеристика растворов высокомолекулярных соединений, истинных и коллоидных растворов
Высокомолекулярные соединения образуют растворы, обладающие свойствами как коллоидных, так и истинных растворов.
Свойства растворов ВМС, характерные для коллоидных растворов:
- размер частиц (молекул ВМС) соответствует размеру коллоидных частиц (10–7 – 10–9 м);
- растворы ВМС не проходят через полупроницаемые мембраны; - явление светорассеивания (размытый конус Тиндаля); - способность к коагуляции; - медленно диффундируют.
Свойства растворов ВМС, характерные для истинных растворов:
- гомогенность; - термодинамическая устойчивость;
- самопроизвольность образования (растворяются в определенных жидкостях, не требуя стабилизаторов); - обратимость коагуляции.
ВМС имеют и специфические свойства – они набухают, их растворы обладают высокой вязкостью и способностью желатинироваться. По современной классификации растворы ВМС относят к гомогенным растворам, имеющим ряд свойств коллоидов и специфические свойства.
5.7.1.3Краткая структура белка
Белки бывают простые и сложные. Простой белок – продукт поликонденсации 20 α-аминокислот. Сложные белки состоят из простого белка и небелковых компонентов.
Различают 4 структуры белка.
Первичная структура белка – это последовательность аминокислот в полипептидной цепи, связанных ковалентной пептидной связью.
Структура полипептидной цепи:

1031
Вторичная структура белка является пространственной структурой, образуется за счет ближнего взаимодействия водородных и дисульфидных связей. Это приводит к образованию α-спиралей и β-структур.
Третичная структура белка образуется за счет дальнего взаимодействия между макромолекулами. Это межмолекулярные, гидрофобные взаимодействия, а также водородные связи. Каждый белок имеет свою специфическую структуру, называемую конформацией.
Четвертичная структура белка образуется из двух и более полипептидных цепей (например, гемоглобин). Объединение таких субъединиц происходит за счет водородных, дисульфидных, гидрофобных связей, сил Ван-дер-Ваальса.
Все белки подразделяются на глобулярные и фириллярные.
Глобулярные белки имеют сферическую или эллипсидную форму, например гемоглобин. Глобулярный белок может содержать неаминокислотный фрагмент – простетическую группу. В гемоглобине – гем.
Фибриллярные белки содержат одну или более полипептидных цепей, молекулы их вытянуты, длина во много раз превышает диаметр. Это структурные белки соединительных, эластичных и сократительных тканей, белки волос и кожи.
5.7.1.4 Белки, как высокомолекулярные электролиты. Изоэлектрическая точка белка и методы ее определения
Молекула белка имеет электрический заряд, обусловленный диссоциацией ионогенных групп (– СООН) и (– NH2): эти группы принадлежат концевым аминокислотам, а также дикарбоновым и диаминовым аминокислотам, расположенным в середине полипептидной цепи. В результате диссоциации образуется биполярный ион (амфиион), имеющий положительный и отрицательный заряд. Схематически диссоциацию можно представить так:
Преобладание в молекуле белка групп – СООН сообщает ему отрицательный заряд, белок проявляет свойства слабой кислоты. Преобладание групп – NH2 сообщает белку положительный заряд и основные свойства.

1032
В зависимости от реакции среды молекула белка заряжается следующим образом:
а) в кислой среде – положительно:
б) в щелочной среде – отрицательно:
Таким образом, заряд белка зависит от реакции среды, соотношения количества карбоксильных групп и степени их диссоциации.
Биполярный ион или амфион принято называть цвиттер-ионом. Значение рН, при котором белок находится в изоэлектрическом
состоянии, т.е. в состоянии, при котором число положительных и отрицательных зарядов одинаково, общий заряд равен нулю, называется
изоэлектрической точкой белка (ИЭТ).
Изоэлектрическая точка является важной характеристикой белков. Каждый белок имеет свою индивидуальную ИЭТ.
Существуют следующие методы ее определения:
1.По электрофоретической подвижности. При проведении электрофореза белок при значении рН, равному ИЭТ, не перемещается в электрическом поле.
2.По степени коагуляции (высаливания). В ИЭТ наблюдается наибольшее помутнение раствора и белок выпадает в осадок.
3.По скорости желатинирования. Желатинирование (или застудневание) происходит быстрее всего в ИЭТ.
4.По величине набухания. Наименьшее набухание белка происходит в пробирке, где рН ближе к ИЭТ.
5.7.1.5 Устойчивость растворов высокомолекулярных соединений. Методы осаждения биополимеров: высаливание, коацервация и их биологическое значение
Основным фактором термодинамической устойчивости растворов биополимеров (ВМС) является их высокая гидрофильность, которая обусловлена наличием таких гидрофильных групп, как – NH2, – COOH, –
OH, – SH, – CO – NH –, пептидные связи и др.
В результате вокруг макромолекулы образуется монослой растворителя, называемый сольватной или гидратной оболочкой. Дополнительным фактором устойчивости является наличие заряда на молекуле белка, обусловленное ионогенными группами. Растворы ВМС самопроизвольно не осаждаются.

1033
Чтобы лишить высокомолекулярные частицы устойчивости, необходимо удалить гидратную оболочку и снять электрический заряд.
Одним из методов осаждения белков является высаливание.
ВЫСАЛИВАНИЕ:
Высаливание – это процесс осаждения белков с помощью концентрированных растворов солей. Для высаливания чаще всего используют соли Na2SO4, (NH4)2SO4, фосфаты.
Высаливание наиболее эффективно в ИЭТ белка, что и используется для её определения. Учитывая механизм осаждающего действия электролитов и других водоотнимающих средств, немецкий биохимик Кройт предложил общую схему высаливания.
Схема высаливания по Кройту:
Из схемы видно, что необходимо удалить гидратную оболочку (спиртом или ацетоном) и снять заряд электролитом. Последовательность этих действий не имеет значения. Для осаждения многих белков достаточно большой концентрации одного электролита, особенно сульфатов, которые обеспечивают снятие и заряда, и дегидратацию частицы.
Высаливающее действие электролитов зависит от способности их ионов гидратироваться. Ученый Гофмейстер установил последовательность высаливающего действия анионов и катионов.
Лиотропный ряд анионов:
SO42– > F– > (цитрат)3– > (тартрат)2– > (ацетат)– > Сl– > NO3– > Br– > CNS–
Лиотропный ряд катионов:
Li+ > Na+ > K+ > Rb+ > Cs+ > Mg2+ > Ca2+ > Sr2+ > Be2+
Процесс высаливания используется для приготовления некоторых лечебных сывороток и противокоревого α-глобулина, а также для разделения белков на фракции при биологических исследованиях.
КОАЦЕРВАЦИЯ:
При снижении растворимости в растворах ВМС наблюдается коацервация – слияние гидратных оболочек нескольких частиц без объединения самих частиц.
Схема коацервации:

1034
Капли или слои, образующиеся в результате коацервации, называются коацервантами. В теории происхождения жизни на Земле, разработанной академиком А.И. Опариным, большое значение придается возникновению белковых коацервантов из белковых молекул.
5.7.1.6 Вязкость растворов ВМС. Вязкость крови
Одним из особых свойств растворов ВМС является вязкость. Вязкость (внутреннее трение) – мера сопротивления среды движению.
Растворы ВМС не подчиняются основным законам вязкого течения – законам Ньютона и Туазейля, обнаруживая так называемую аномальную вязкость. Вязкость растворов ВМС очень высока в сравнении с растворами низкомолекулярных веществ. Большая вязкость растворов ВМС обусловлена их высокой гидрофильностью, макромолекулы прочно связаны с молекулами растворителя. На вязкость также влияет форма молекул. Если длинные макромолекулы расположены перпендикулярно потоку, то эффект сопротивления наибольший, если вдоль потока – сопротивление наименьшее.
При увеличении давления частицы ориентируются вдоль потока и вязкость уменьшается. В более концентрированных растворах полимеров образуются пространственные структурные сетки, увеличивающие вязкость растворов.
Вязкость растворов ВМС зависит от концентрации раствора. Для низкомолекулярных веществ эта зависимость выражается уравнением Эйнштейна: η = η0 ( 1 + α С ), где η – вязкость раствора, η0 – вязкость растворителя, α – коэффициент, зависящий от формы частиц, С – концентрация раствора полимера. Увеличение вязкости, связанное с изменением концентрации при растворении полимера характеризуют удельной вязкостью (формула 5.7.1):
(5.7.1)
Штаудингер установил следующую зависимость удельной вязкости от молекулярной массы полимера (формула 5.7.2):
(5.7.2)
К - константа, характерная для полимергомологического ряда, М – молекулярная масса, С – концентрация вещества в растворе.
Уравнение Штаудингера используют для определения молекулярной массы биополимеров. Вязкость растворов белков зависит от величины рН.

1035
Наименьшей вязкостью растворы белков обладают в области изоэлектрическойточки, так как макромолекулы свернуты в плотные клубки, оказывающие наименьшее сопротивление течению жидкости.
ВЯЗКОСТЬ КРОВИ.
Вязкость воды при t° = 20°C составляет 1 мПа × с, а вязкость крови в норме – 4-5 мПа × с. При различных патологиях значения вязкости крови могут изменяться от 1,7 до 22,9 мПа × с. Неоднородность структуры крови, специфика строения и разветвления кровеносных сосудов приводит к сложному распределению вязкости крови, движущейся по сосудистой системе. Вязкость крови зависит от многих факторов: температуры, наличия тромбоцитов и белых кровяных телец (не только при патологии).
Вязкость увеличивается при сгущении крови, т.е. при потере воды. У больных с хроническими формами ишемической болезни сердца вязкость крови повышены, при физических нагрузках она уменьшается.
В последние годы в медицинской практике измерение вязкости крови используется для изучения ее реологических свойств при тяжелых интоксикациях.
Для измерения вязкости используют специальные приборы – вискозиметры.
5.7.1.7 Коллоидно-осмотическое давление в растворах ВМС. Мембранное равновесие Доннана
Осмотическое давление, как свойство коллигативное, зависит от числа частиц в единице объема системы. Осмотическое давление в растворах собственно коллоидов очень низкое, так как низкая концентрация частиц в растворе из-за их большого размера в сравнении с молекулами.
Так, осмотическое давление 1% раствора сахарозы равно 79,46 кПа, а 1% раствор золя сульфида мышьяка – 0,0034 кПа. Осмотическое давление в растворах белков и других высокомолекулярных соединений значительно выше, чем в коллоидах. Так, 1% раствор желатины имеет давление, равное 1,02 кПа. Для очень разбавленных растворов полимеров осмотическое давление подчиняется уравнению Вант-Гоффа:
C повышением концентрации осмотическое давление полимеров подчиняется более сложному уравнению (5.7.3):
(5.7.3)
где, С – массовая концентрация ВМС, М – молекулярная масса, К – константа, зависящая от свойств растворителя. Данное уравнение используется для определения молекулярной массы полимеров.
Осмотическое давление в растворах белков оказывает существенное влияние на ряд процессов в организме. Часть осмотического давления крови,

1036
обусловленная белками, называется онкотическим давлением. Оно невелико и составляет 0,5% (3,5-3,9 кПа) от общего осмотического давления крови.
Онкотическое давление играет определённую роль в жизнедеятельности организма. При отклонении его от нормы возникают отёки. При понижении белка в крови вследствие голодания или потери белка с мочой при заболевании почек возникает разница онкотического давления в крови и в соединительной ткани, вода из русла крови попадает в соединительную ткань и образуются отеки.
Изучение осмотических свойств организма показало, что внутри клетки осмотическое давление всегда выше, чем во внеклеточной жидкости.
Присутствие в организме солей белков, отделенных мембранной от растворов электролитов приводит к перераспределению электролитов и, таким образом, влияет на осмотическое давление по обе стороны мембраны.
Перераспределение электролитов подчиняется выведенному Доннаном уравнением мембранного равновесия (формула 5.7.4):
(5.7.4)
где Х – количество ионов, перешедших в клетку, Свн – концентрация ионов во внеклеточной жидкости, Скл – концентрация ионов в клетке.
Анализ уравнения показывает:
1. Если до начала перераспределения Свн >> Скл, то в знаменателе уравнения можно пренебречь слагаемым Скл. Тогда получим выражение
(5.7.5):
(5.7.5)
т.е. во внутрь клетки переходит половина ионов из внешней среды.
2.Если до начала перераспределения Скл >> Свн, то числитель будет малой величиной, а Х ещё меньше. И в этом случае внутрь клетки перейдет какое-то количество ионов, зависящее от соотношения Скл и Свн.
3.Если Скл = Свн, то уравнение имеет вид выражения (5.7.6):
(5.7.6)
В этом случае перейдет в клетку третья часть ионов из внешнего раствора.
Таким образом, внутри клетки количество ионов всегда больше, чем снаружи. Этим объясняется повышенное осмотическое давление клетки по

1037
сравнению с давлением окружающей клетки жидкости. Это обстоятельство поддерживает тургор клеток.
Эффект Доннана (т.е. неравномерное распределение электролитов между клетками и омывающей их жидкостью) оказывает большое влияние на жизнедеятельность клеток, на величину биопотенциалов, распределение электролитов и пр. наряду с физиологическими механизмами.
5.7.1.8 Набухание и растворение ВМС. Механизм набухания. Факторы, влияющие на набухание. Биологическое значение набухания
Процесс растворения ВМС является самопроизвольным, но проходит через стадию набухания. Набухание – это увеличение объема полимера в результате избирательного поглощения низкомолекулярного растворителя. Этот процесс характеризуется степенью набухания (α) (формула 5.7.7):
(5.7.7)
где m0 – масса полимера до набухания, m – масса полимера после набухания.
Теория растворов ВМС рассматривает набухание и растворение полимеров как процесс смешения двух жидкостей. Молекулы низкомолекулярного растворителя проникают в полимер, раздвигают звенья цепи и ослабляют межмолекулярное взаимодействие, поэтому полимер увеличивается в массе и объеме. Процесс набухания проходит в две стадии. Первая стадия – поглощение небольшого количества растворителя, которое идет на образование сольватной оболочки. На I стадии выделяется теплота, называемая теплотой набухания. На I стадии происходит уменьшение суммарного объема полимера и растворителя. Растворитель в сольватной оболочке изменяет свои физико-химические свойства (плотность, температура замерзания и др.). На II стадии поглощается много жидкости без выделения тепла. На этой стадии наблюдается увеличение объема системы, которое может заканчиваться полным растворением.
Набухание может быть ограниченным и неограниченным. Неограниченное набухание – это набухание, заканчивающееся
полным растворением. Процесс сопровождается увеличением энтропии системы.
Ограниченное набухание – это набухание, не переходящее в растворение. Оно заканчивается образованием эластичного студня.
Примером неограниченного набухания являются альбумины, желатина в горячей воде. Ограниченно набухает желатина в воде при комнатной температуре.
На процесс набухания влияют ряд факторов: температура, рН среды, наличие электролитов. В области ИЭТ белка набухание минимальное.
Температура ускоряет процесс набухания. По влиянию на процесс набухания белков анионы располагаются в лиотропный ряд: CNS– > I– > Br– > Cl– > ClO4– > SO2–.
1038
Процесс набухания играет важную роль в физиологии организма. Соединительная ткань способна вследствие набухания воспринимать излишек воды или отдавать его клеткам и крови, т.е. является регулятором водного обмена между кровью и клетками.
5.7.1.9 Застудневание растворов ВМС. Факторы, влияющие на застудневание. Тиксотропия. Синерезис. Биологическое значение этих процессов
Большинство растворов ВМС, таких как агар-агар, желатина, а также коллоидные растворы типа гидроксида железа (III) или кремниевые кислоты, способны при определенных условиях переходить в твердое состояние без видимого разделения фаз. Этот процесс носит название застудневание или желатинирование. А продукты, образовавшиеся в результате этих процессов, называются студнями или гелями.
Студни или гели – это дисперсные системы, у которых частицы дисперсной фазы не движутся свободно, а связаны между собой, т.е. это золи, потерявшие агрегативную устойчивость, но сохранившие кинетическую устойчивость.
Гели могут быть естественного и искусственного происхождения. К числу естественных относятся цитоплазма живых клеток, кожа, хрусталик глаза и т.д. Искусственные гели можно приготовить из желатины, агар-агара, каучука. Многие продукты питания представляют собой студни (хлеб, сыр, джемы и т.д.).
Причиной застудневания является возникновение связей между молекулами ВМС. Связи могут быть гидрофобные, водородные, ионные. Они зависят от природы вещества и условий застудневания. Застудневание можно определить, как процесс образования и упрочнения пространственной сетки.
Наличие у студней пространственной сетки подтверждается результатами исследования скорости диффузии. В студнях невысоких концентраций диффузия низкомолекулярных веществ происходит почти с такой же скоростью, как и в чистом растворителе. С увеличением концентрации студня скорость диффузии уменьшается. На этих свойствах основано приготовление полупроницаемых мембран, используемых для диализа. Диффузия в гелях и студнях лежит в основе разделения молекул по размеру – гель-фильтрация.
Процесс застудневания зависит от следующих факторов: формы и природы ВМС, концентрации, температуры, наличия электролитов, рН среды. Лучше всего застудневание происходит в ИЭТ. Ионы, увеличивающие набухание, замедляют застудневание. Лиотропный ряд анионов следующий: SO42– > (цитрат)3– > (тартрат)2– > (ацетат)– > Сl– >
NO3– > Br– > I– > CNS–.
Понижение температуры способствует застудневанию.
1039
Студни под влиянием механических воздействий способны разжижаться, переходить в золи, а затем при хранении снова застудневать. Такое явление получило название тиксотропии. Тиксотропия – одно из доказательств того, что структурообразование в гелях происходит за счет межмолекулярных взаимодействий.
Застудневание системы, происходящее самопроизвольно, не всегда является конечной стадией. Студни со временем меняют свои свойства, т.е. стареют. Происходит разделение студня на две фазы: уплотнённый гель и разведённый золь. Этот процесс называется синерезисом. Структурная сетка геля стягивается и выжимает из себя растворитель. У белков синерезис зависит от рН и активнее всего в ИЭТ.
Биологическое значение процессов старения студней очень важно, так как при этом происходит их уплотнение, что отражается на проницаемости клеточных мембран и цитоплазмы. Снижение проницаемости нарушает обмен веществ между клеткой и окружающей средой. Появление у тканей с увеличением возраста организма таких качеств, как большая жесткость и меньшая эластичность, объясняется процессами синерезиса и дегидратации.

1040
ПРАКТИЧЕСКИЙ РАЗДЕЛ
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ ЛАБОРАТОРНЫХ ЗАНЯТИЙ
РАЗДЕЛ ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОБЩЕЙ ХИМИИ. ХИМИЯ ПРОСТЫХ ВЕЩЕСТВ И СОЕДИНЕНИЙ ЭЛЕМЕНТОВ
Лабораторное занятие № 1 (4 ЧАСА)
Введение. Основные понятия и законы химии
ЦЕЛЬ: ознакомиться с техникой безопасности в лаборатории неорганической химии. Изучить основные стехиометрические законы. Закон сохранения массы веществ в химических реакциях. Закон постоянства состава вещества. Закон эквивалентов. Газовые законы: закон объемных отношений, закон Авогадро, объединенный газовый закон, закон парциальных давлений. Современное содержание стехиометрических законов, их применимость к веществам с различной структурой.
ОБОРУДОВАНИЕ: инженерный калькулятор. ПЛАН
1.Техника безопасности в химической лаборатории.
2.Основные стехиометрические законы.
3.Газовые законы.
4.Разбор и решение задач по теме: «Стехиометрические законы».
5.Индивидуальные задания для самостоятельной работы.
Лабораторное занятие № 2 (4 ЧАСА)
Основные классы неорганических соединений
ЦЕЛЬ: ознакомиться со свойствами и методами получения оксидов, кислот, солей, оснований, а также проследить генетическую связь между классами неорганических соединений.
ОБОРУДОВАНИЕ: штатив с пробирками, промывалка, спиртовка. РЕАКТИВЫ: оксид цинка, гранулы Zn, порошок гашеной извести
Ca(OH)2, водные |
растворы NaOH, ZnSO4, AICl3, |
FeCl3, HCl, |
H2SO4 универсальная |
индикаторная бумага, раствор |
фенолфталеина, |
метилоранжа, дистиллированная вода. |
|
|
ПЛАН |
|
|
1.Получение и свойства оксидов и гидроксидов.
2.Получение и свойства гидроксидов.
3.Получение солей.
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
Лабораторное занятие № 3 (2 ЧАСА)
Строение атома
ЦЕЛЬ: ознакомиться с основными положениями современной теории
1041
строения атома. Изучить состав атомных ядер. Нуклиды и изотопы. Явление радиоактивности.
ПЛАН
1.Строение электронных оболочек атомов.
2.Принцип Паули и максимальная емкость электронных оболочек.
3.Правило Хунда.
4.Электронные конфигурации и электронно-графические формулы
атомов.
5.Перечень вопросов для самоподготовки.
Лабораторное занятие № 4 (2 ЧАСА)
Периодический закон и периодическая система элементов
ЦЕЛЬ: Изучить особенности заполнения атомных орбиталей электронами и формирование периодов, s-, p-, d-, f- элементы, их расположение в периодической системе.
ПЛАН
1.Структура периодической системы и ее современные графические
формы.
2.Положение металлов и неметаллов в периодической системе.
3.Основные факторы, определяющие характер изменения свойств химических элементов.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 5 (2 ЧАСА)
Химическая связь и строение вещества
ЦЕЛЬ: изучить основные типы химической связи: ковалентная, ионная и металлическая. Количественные характеристики химической связи: длина, энергия.
ПЛАН
1.Ковалентная химическая связь.
2.Свойства ковалентной связи.
3.Основы метода молекулярных орбиталей (МО).
4.Ионная и металлическая связь.
5.Водородная связь.
6.Перечень вопросов для самоподготовки.
Лабораторное занятие № 6 (4 ЧАСА)
Скорость химических реакций
ЦЕЛЬ: изучить зависимость скорости химической реакции от концентраций реагирующих веществ, влияние температуры на скорость химической реакции, влияние размера поверхности реагирующих веществ на скорость химической реакции, влияние катализатора на скорость химической реакции, смещение химического равновесия при изменениях концентраций
1042
участвующих в реакции веществ, смещение химического равновесия при изменении среды.
ОБОРУДОВАНИЕ: секундомер, ступка с пестиком, стеклянная палочка, пробирки, стакан на 200 мл.
РЕАКТИВЫ: хлорид железа (III), иодид калия, тиосульфат натрия, гидроксид натрия, серная кислота свежеприготовленный раствор крахмала, раствор пероксида водорода, кристаллический нитрат свинца, кристаллический иодид калия, дистиллированная вода.
ПЛАН
1.Зависимость скорости химической реакции от концентрации реагирующих веществ.
2.Влияние температуры на скорость химической реакции.
3.Влияние размера поверхности реагирующих веществ на скорость химической реакции
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
Лабораторное занятие № 7 (2 ЧАСА)
Химическое равновесие
ЦЕЛЬ: ознакомиться с обратимыми и необратимыми химическими реакциями. Состоянием химического равновесия. Константой химического равновесия. Факторами, влияющими на величину константы равновесия: природа реагентов и температура.
ПЛАН
1.Обратимые и необратимые химические реакции.
2.Константа химического равновесия.
3.Факторы, влияющие на величину константы равновесия: природа реагентов и температура.
4.Влияние изменения концентрации, давления и температуры на положение химического равновесия.
5.Принцип Ле-Шателье.
6.Перечень вопросов для самоподготовки.
Лабораторное занятие № 8 (2 ЧАСА)
Основы химической термодинамики
ЦЕЛЬ: изучить основные термодинамические характеристики. Внутреннюю энергию системы и ее изменение в ходе химических превращений. Энтальпию. Стандартную энтальпию образования вещества. Изменение энтальпии в системах в ходе химических превращений. Тепловой эффект химических реакций. Экзо- и эндотермические процессы. Закон Гесса.
ОБОРУДОВАНИЕ: инженерный калькулятор. ПЛАН 1. Внутренняя энергия системы
1043
2.Энтальпия.
3.Экзо- и эндотермические процессы
4.Закон Гесса
5.Разбор и решение задач по теме: «Термохимические расчеты»
6.Индивидуальные задания для самостоятельной работы.
Лабораторное занятие № 9 (4 ЧАСА)
Состав растворов. приготовление и определение концентрации раствора
ЦЕЛЬ: изучить основные способы приготовления растворов и определения их концентрации.
ОБОРУДОВАНИЕ: весы, микрокалькулятор, ареометр жидкостей тяжелее воды, термометр на 100ºС, фарфоровая ступка с пестиком, мерная колба емкостью 250 мл, мерные цилиндры емкостью 50 и 250 мл, цилиндр высокий и узкий, стаканы емкостью 100мл и 300 мл, воронка, склянки и банки для сливания растворов, стеклянная палочка, ложки.
РЕАКТИВЫ: Хлорид бария BaCl2*2H2O, карбонат натрия кристаллический Na2CO3*10H2O, серная кислота H2SO4, соляная кислота HCI (p = 1.19 г/см), гидроксид натрия NaOH (40%), хлорид натрия NaCI (20% и
5%).
ПЛАН
1.Приготовление растворов с заданной массовой долей вещества в
растворе.
2.Приготовление растворов определенной молярной и нормальной концентрации
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 10 (4 ЧАСА)
Диссоциация электролитов. Понятие буферные растворы
ЦЕЛЬ: приготовить буферные растворы с различным значением рН. Определить влияние разбавления, добавления сильных электролитов на значение рН буферных растворов. Определить потенциометрически изменение рН буферных растворов с различным соотношением кислоты и соли при добавлении сильной кислоты или сильного основания. Опредить буферную ёмкость раствора.
ОБОРУДОВАНИЕ: рН-метр, колбы, пипетки, воронка, склянки и банки для сливания растворов, стеклянная палочка, ложки.
РЕАКТИВЫ: 0,1 М растворы уксусной кислоты, ацетата натрия, гидро- и дигидрофосфатов натрия, аммиака и хлорида аммония, дистиллированная вода.
ПЛАН
1.Приготовление буферных растворов.
2.Влияние разбавления на рН буферных растворов
3.Оформление отчета лабораторной работы.
1044
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 11 (4 ЧАСА)
Гидролиз солей
ЦЕЛЬ: ознакомиться с явлениями гидролиза солей и практическими следствиями этого явления.
ОБОРУДОВАНИЕ: колбы, пипетки, пробирки, стеклянная палочка. РЕАКТИВЫ: раствор хлорида аммония, ацетата натрия, хлорида
натрия, карбоната натрия, воды, универсального индикатора, раствор сульфата цинка, раствор гидроксида калия, хлорида железа (III).
ПЛАН
1.Различные случаи гидролиза солей.
2.Влияние концентрации раствора на степень гидролиза соли.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 12 (2 ЧАСА)
Произведение растворимости водородный показатель
ЦЕЛЬ: ознакомиться с константой диссоциации, ионным произведением воды, водородным показателям (рН).
ОБОРУДОВАНИЕ: инженерный калькулятор. ПЛАН
1.Ионное произведение воды.
2.Водородный показатель (рН).
3.Константа диссоциации.
4.Разбор и решение задач по теме: «Ионное произведение воды. Водородный показатель (рН)»
5.Индивидуальные задания для самостоятельной работы.
Лабораторное занятие № 13 (4 ЧАСА)
Окислительно–восстановительные процессы
ЦЕЛЬ: научиться оценивать условия протекания окислительновосстановительных реакций.
ОБОРУДОВАНИЕ: штатив с пробирками.
РЕАКТИВЫ: растворы пероксида водорода, перманганата калия, иодида калия (или натрия), нитрита калия (или натрия), серной кислоты (разб), гидроксида калия (конц), бромида калия (или натрия), хлорида железа (III); иод кристаллический.
ПЛАН
1.Окислительно-восстановительная двойственность пероксида водорода и нитритов.
2.Зависимость характера продуктов окислительновосстановительной реакции от рН среды.
3.Оформление отчета лабораторной работы.
1045
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 14 (2 ЧАСА)
Электрохимические процессы
ЦЕЛЬ: определить направления протекания окислительновосстановительных реакций, влияние рН среды на величину окислительновосстановительного потенциала и состав образующихся продуктов.
ПЛАН
1.Электродные потенциалы.
2.Влияние рН среды.
3.Электролиз.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 15 (4 ЧАСА)
Комплексные соединения
ЦЕЛЬ: экспериментальное ознакомление с методами получения комплексных соединений, а также изучение их свойств.
ОБОРУДОВАНИЕ: штатив с пробирками.
РЕАКТИВЫ: раствор сульфата меди (II), раствор аммиака, раствор гексацианоферрата (II) калия, сульфата никеля (II), хлорида железа (III), раствор перманганата калия.
ПЛАН
1.Получение соединения с комплексным анионом и катионом.
2.Исследование прочности комплексных ионов.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 16 (2 ЧАСА)
Водород и элементы VII А группы
ЦЕЛЬ: ознакомление с физическими и химическими свойствами элементов VII А группы; решение задач.
ПЛАН
1.Общая характеристика элементов группы VIIA.
2.Природные ресурсы, физические и химические свойства галогенов.
3.Соединения галогенов с водородом.
4.Биологическая роль и применение соединений элементов группы
VII A.
5.Перечень вопросов для самоподготовки.
Лабораторное занятие № 17 (4 ЧАСА)
Химия простых веществ и соединений неметаллов
ЦЕЛЬ: экспериментальное ознакомление с химическими свойствами соединений неметаллов.
1046
ОБОРУДОВАНИЕ: штатив с пробирками.
РЕАКТИВЫ: порошок серы, концентрированная азотная кислота, раствор хлорида бария, раствор перманганата калия, концентрированная серная кислота, порошок сульфита натрия, магниевая стружка, гранулы цинка, медная проволока, порошок гидроксида натрия, концентрированная соляная кислота, раствор дихромата калия, раствор аммиака, раствора нитрита натрия, раствор йодида калия, раствор карбоната натрия, раствор хлорида кальция, раствор силиката натрия, раствор хлорида олова (II), раствор нитрата свинца (II), кристаллы олова, кристаллы свинца.
ПЛАН
1.Восстановительные свойства серы.
2.Изучение свойств соединений серы (IV).
3.Изучение свойств серной кислоты.
4.Получение и обнаружение аммиака.
5.Восстановительные свойства аммиака.
6.Окислительные свойства нитритов.
7.Взаимодействие азотной кислоты с металлами.
8.Получение малорастворимых карбонатов.
9.Получение кремниевой кислоты.
10.Получение олова и свинца.
11.Оформление отчета лабораторной работы.
12.Перечень вопросов для самоподготовки.
Лабораторное занятие № 18 (4 ЧАСА)
Химические свойства металлов
ЦЕЛЬ: экспериментальное ознакомление с химическими свойствами соединений металлов.
ОБОРУДОВАНИЕ: штатив с пробирками.
РЕАКТИВЫ: растворы Na2CO3, NaHCO3 и K2CO3, кусочек магниевой ленты, фенолфталеин, раствор хромата калия, раствор дихромата калия, раствор хлорида бария, раствор серной кислоты, раствор щелочи, порошок сульфита натрия порошок сульфата железа (II).
ПЛАН
1.Гидролиз карбонатов и гидрокарбонатов щелочных металлов.
2.Взаимодействие магния с водой.
3.Соединения хрома (VI).
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
1047
РАЗДЕЛ ОРГАНИЧЕСКАЯ ХИМИЯ
I. ВВЕДЕНИЕ. ОБЩИЕ ПРЕДСТАВЛЕНИЯ
Лабораторное занятие № 1 (2 ЧАСА)
Предмет органической химии. Строение органических соединений
ЦЕЛЬ: техника безопасности в лаборатории органической химии; дать представление о составе органических веществ, рассмотреть многообразие органических веществ; рассмотреть основные типы структурных фрагментов органических молекул: простые и кратные связи, углеродные цепи и циклы, функциональные группы; структурные формулы как средство отображения строения органических соединений.
ОБОРУДОВАНИЕ: инженерный калькулятор. ПЛАН
1.Техника безопасности в химической лаборатории.
2.Состав органических веществ.
3.Основные положения теории строения органических соединений.
4.Разбор и решение задач по теме: «Вывод структурных формул».
5.Индивидуальные задания для самостоятельной работы.
Лабораторное занятие № 2 (1 ЧАС)
Классификация органических соединений
ЦЕЛЬ: рассмотреть основные признаки классификации: скелет молекулы, степень насыщенности, наличие функциональных групп; дать представление об основных классах органических веществ.
ПЛАН
1.Основные признаки классификации органических соединений.
2.Основные классы органических веществ.
3.Перечень вопросов для самоподготовки.
Лабораторное занятие № 3 (1 ЧАС)
Основы номенклатуры орагических соединений
ЦЕЛЬ: дать представление о тривиальных и систематических названиях органических соединений, о заместительной номенклатуре IUPAC; рассмотреть основные принципы построения названий органических соединений; дать понятие о родоначальной структуре, о характеристических группах; закрепить названия функциональных групп, нефункциональных заместителей, насыщенных и ненасыщенных углеводородных групп; дать представление о старшинстве функциональных групп и о принципах радикало-функциональной номенклатуры.
ПЛАН
1.Номенклатура органических соединений.
2.Названия функциональных групп, нефункциональных заместителей, насыщенных и ненасыщенных углеводородных групп.
1048
3.Принципы радикало-функциональной номенклатуры.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 4 (2 ЧАСА)
Изомерия органических соединений
ЦЕЛЬ: дать представление о типах изомерии: структурная и пространственная и способах изображения пространственного строения молекул, а также пространственную изомерию алкенов: цис-, транс- и Z-, E- номенклатуры.
ПЛАН
1.Изомерия органических соединений.
2.Стериоизомерия и пространственная изомерия органических соединений.
3.Перечень вопросов для самоподготовки.
Лабораторное занятие № 5 (6 ЧАСОВ)
Методы выделения, очистки и идентификации органических соединений
ЦЕЛЬ: ознакомиться с основными методами выделения и очистки органических веществ; определить качественный состав органических веществ, используя методы качественного элементного анализа органических соединений.
ОБОРУДОВАНИЕ: набор пробирок, пробиркодержатель, спиртовка, круглодонная колба на 100 мл, стакан на 100 мл, обратный холодильник, «кипелки», стеклянная палочка, баня, плитка, воронка Бюхнера, колба Бунзена, фильтровальная, газоотводные трубки с пробками для пробирок, вата, спички, пинцеты, пипетки, медная проволока.
РЕАКТИВЫ: твердое термоустойчивое вещество, набор растворителей (вода, этанол, ацетон, хлороформ, четырехлористый углерод, бензол, толуол, гексан, диэтиловый эфир, петролейный эфир, этилацетат, диоксан, ледяная уксусная кислота); сахароза, оксид меди (ІІ), известковая вода; безводный сульфат меди (ІІ), мочевина, тиомочевина, металлический натрий, этиловый спирт, 5% раствор сульфата железа (ІІ), 1% раствор хлорида железа (ІІІ), 10% соляная кислота, спиртовой раствор фенолфталеина, 2% раствор ацетата свинца, 2 н раствор гидроксид натрия, 2% раствор нитропруссида натрия, 10% уксусная кислота, йодоформ или хлороформ, концентрированная азотная кислота, 1% раствор нитрата серебра
ПЛАН
1.Освоить и применить основные методы очистки, выделения и идентификации органических соединений.
2.Провести качественный элементный анализ органических
соединений.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
1049
II. УГЛЕВОДОРОДЫ
Лабораторное занятие № 6 (10 ЧАСОВ)
Алканы. Алкены. Алкины. Алициклические углеводороды
ЦЕЛЬ: познакомиться с лабораторными способами получения некоторых представителей гомологических рядов предельных, этиленовых и ацетиленовых углеводородов и изучить их свойства. Сравнить реакционную способность алканов, алкенов и алкинов.
ОБОРУДОВАНИЕ: ступка, пестик, газоотводная трубка с пробкой, стеклянная лопатка, набор пробирок в штативе, спиртовка, вытяжной шкаф.
РЕАКТИВЫ: обезвоженный ацетат натрия; натронная известь, насыщенный раствор бромной воды, 1% раствор перманганата калия, 5% раствор брома в четыреххлористом углероде, концентрированные кислоты: соляная, серная, азотная, концентрированный раствор аммиака, 1 н раствор карбоната натрия, 0,2 н раствор нитрата серебра, аммиачный раствор хлорида меди (I), 1% спиртовой раствор фенолфталеина, лакмусовая бумага синяя, пентан (гексан, гептан), жидкий непредельный углеводород, керосин, жидкий ацетиленовый углеводород (фенилацетилен), песок.
ПЛАН
1.Химические свойства алканов, алкенов, алкинов.
2.Получение и изучение свойств углеводородов.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 7 (6 ЧАСА)
Ароматические углеводороды (арены)
ЦЕЛЬ: познакомиться с лабораторным способом получения бензола. Изучить некоторые физические и химические свойства бензола и его гомологов. Сравнить реакционную способность бензола и толуола. Познакомиться со свойствами полиядерных ароматических соединений на примере нафталина.
ОБОРУДОВАНИЕ: газоотводная трубка, набор пробирок, выпарительная чаша, стаканы объемом 100 мл, спиртовка.
РЕАКТИВЫ: бензол, толуол, ксилол, нафталин, хлорбензол, хлористый бензил, концентрированные кислоты: серная, азотная, соляная, 10% раствор брома в четыреххлористом углероде, бромная вода, 1% раствор перманганата калия,0,2 н раствор нитрата серебра, натронная известь, лакмусовая бумага, лед.
ПЛАН
1.Химические и физические свойства бензола и его гомологов.
2.Получение и изучение свойств бензола.
3.Изучение свойств нафталина.
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
1050
III. ГОМОФУНКЦИОНАЛЬНЫЕ СОЕДИНЕНИЯ
Лабораторное занятие № 8 (4 ЧАСА)
Галогенпроизводные углеводородов
ЦЕЛЬ: ознакомиться со способом непрямого галогенирования спиртов, научиться выделять полученный продукт из реакционной смеси.
ОБОРУДОВАНИЕ: установка для синтеза, электрическая плитка, делительная воронка, воронка, мерный цилиндр (50 см3), мерный цилиндр (100 см3), ёмкость для отходов, капельница, штатив с пробирками (20 шт.), колба-приемник, фильтровальная бумага, пробка с хлоркальциевой трубкой.
РЕАКТИВЫ: спирт этиловый, 5% раствор азотной кислоты, концентрированная серная кислота, 10% раствор уксусной кислоты, 1 н раствор гидроксида натрия, калий бромистый (тв.), кальций хлористый безводный, 2% раствор нитрата серебра, иодид натрия (тв.), ацетон, лед, вода дистиллированная.
ПЛАН
1.Провести синтез бромэтана.
2.Качественные реакции на определение галогеналканов.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 9 (4 ЧАСА)
Спирты, фенолы, простые эфиры
ЦЕЛЬ: изучить некоторые физические и химические свойства предельных одноатомных и многоатомных спиртов и фенолов. Оценить взаимное влияние гидроксильной группы и бензольного ядра. Отметить качественные реакции на спирты и фенолы.
ОБОРУДОВАНИЕ: набор пробирок, пробка с газоотводной трубкой, стаканчик (100 мл), пипетки, водяная баня, спиртовка, предметное стекло, фарфоровая чашка, спички.
РЕАКТИВЫ: спирты: этиловый, изоамиловый, глицерин, металлический натрий; 1% спиртовой раствор фенолфталеина, безводный и 2 н раствор сульфата меди (II), концентрированный и 2 н раствор серной кислоты, концентрированный раствор азотной кислоты, 2 н раствора соляной кислоты, 2 н раствор гидроксида натрия, медная проволока, песок, фенол, пирокатехин, резорцин, гидрохинон, пирогаллол, бромная вода, синяя лакмусовая бумага.
ПЛАН
1.Химические свойства спиртов.
2.Физические и химические свойства фенолов.
3.Получение простого эфира.
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
1051
Лабораторное занятие № 10 (4 ЧАСА)
Алифатические и ароматические амины
ЦЕЛЬ: научиться получать амины жирного ряда и изучить свойства алифатических и ароматических аминов.
ОБОРУДОВАНИЕ: колбы Вюрца, лед, лучина, стеклянные палочки, холодильник, стаканы, термометр на 2000С, песочная баня, водоструйный насос, пробирки.
РЕАКТИВЫ: концентрированный раствор гидроксида натрия, 10% раствор гидроксида натрия, 1% раствор хлорида железа (III), бромная вода, хлорная известь, селедочный рассол, фенолфталеин, лакмус, кислоты: серная (конц., 50%, разб.), соляная (конц.); анилин, хлороформ, формалин (конц.).
ПЛАН
1.Получение и изучение свойств аминов жирного ряда.
2.Изучение свойств ароматических аминов.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
Лабораторное занятие № 11 (4 ЧАСА)
Карбонильные соединения. Альдегиды и кетоны
ЦЕЛЬ: получить лабораторным способом ацетальдегид и ацетон. Изучить некоторые физические и химические свойства алифатических и ароматических альдегидов, ацетона. Сравнить восстановительную способность альдегидов и кетонов. Познакомиться с характерными реакциями на альдегиды и кетоны.
ОБОРУДОВАНИЕ: набор пробирок, пробка с газоотводной трубкой, стаканы, спиртовка, пробиркодержатель, фильтровальная бумага.
РЕАКТИВЫ: карбид кальция (тв.); 10% раствор серной кислоты; концентрированный раствор аммиака;10% раствор гидроксида натрия; 0,2 н раствор сульфата меди (II); 0,1 н раствор нитрата серебра; оксид ртути (II); дихромат калия (тв.); 40% водный раствор формальдегида; бензальдегид; фуксинсернистая кислота; ацетон; диэтилкетон; этиловый спирт; обезвоженный ацетат натрия; 1% раствор йода в йодистом калии, раствор брома.
ПЛАН
1.Строение и химические свойства альдегидов и кетонов.
2.Получение ацетальдегида.
3.Получение ацетона.
4.Оформление отчета лабораторной работы.
5.Перечень вопросов для самоподготовки.
1052
Лабораторное занятие № 12 (4 ЧАСА)
Карбоновые кислоты и их производные
ЦЕЛЬ: изучить некоторые физические и химические свойства одно- и многоосновных карбоновых кислот, и их функциональных производных: ангидридов кислот, сложных эфиров.
ОБОРУДОВАНИЕ: набор пробирок, пробка с газоотводной трубкой, химические стаканы (100 мл), стеклянная палочка, изогнутая стекляная трубка, пробиркодержатель, спиртовка, спички, водяная баня, «кипелки», вата.
РЕАКТИВЫ: 2 н раствор уксусной кислоты, ледяная уксусная кислота, 2 н раствор муравьиной кислоты, бензойная кислота (кр.), 2 н раствор щавелевой кислоты, щавелевой кислота (кр.), концентрированный раствор соляной кислоты, 2 н раствор соляной кислоты, концентрированный раствор серной кислоты, 2 н раствор серной кислоты, 10 % раствор хлорида железа (III), карбонат натрия (порошок); безводный ацетат натрия; 1 % раствор нитрата серебра, 10 % раствор гидроксида натрия, 5 % раствор аммиака 15 % спиртовой раствор гидроксида натрия; насыщенный водный раствор гидроксида кальция (или бария); глицерин, этиловый и изоамиловый спирты; растворы индикаторов: лакмус, метиловый оранжевый, фенолфталеин; уксусный ангидрид; бромная вода; раствора перманганата калия, магний (стружка), насыщенный раствор мыла, лёд.
ПЛАН
1.Изучить физические и химические свойства одно- и многоосновных карбоновых кислот, и их функциональных производных.
2.Оформление отчета лабораторной работы.
3.Перечень вопросов для самоподготовки.
Лабораторное занятие № 13 (4 ЧАСА)
Углеводы. Полисахариды
ЦЕЛЬ: доказать строение альдоз и кетоз, проведя качественные реакции на углеводы. Изучить кислотный гидролиз ди- и полисахаридов.
ОБОРУДОВАНИЕ: фарфоровая ступка с пестиком, набор пробирок, химические стаканы (100 мл); асбестовая сетка, спиртовка, плитка.
РЕАКТИВЫ: 5% растворы глюкозы, фруктозы, лактозы и сахарозы; концентрированные и 2 н растворы соляной и серной кислот; 10% раствор гидроксида натрия; концентрированный раствор аммиака; 0,2 н раствор нитрата серебра; 10% растворы хлорида кальция и сульфата меди (II); 1% раствор крахмала; раствор йода в йодистом калии; вата или фильтровальная бумага.
ПЛАН
1.Опытным путем доказать строение альдоз и кетоз.
2.Изучить кислотный гидролиз ди- и полисахаридов.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
1053
Лабораторное занятие № 14 (4 ЧАСА)
Аминокислоты
ЦЕЛЬ: изучить способности аминокислот как гетерофункциональных соединений, являющихся структурными компонентам пептидов и белков; научиться проводить качественные реакции на аминокислоты и белки.
ОБОРУДОВАНИЕ: штатив с пробирками, спиртовка, спички. РЕАКТИВЫ: 1% раствор глицина, медный купорос кристаллический,
ацетат натрия кристаллический, 0,2% раствор метилового красного, формалин, 10% раствор гидроксида натрия, 4% раствор белка, 0,1% раствор нингидрина, 1% раствор СuSO4, 3% раствор фенола, концентрированная HNO3; яичный белок, 5% раствор сахарозы; концентрированная H2SO4, ледяная CH3COOH, 2% раствор желатина, 10% раствор ацетата свинца.
ПЛАН
1.Исследовать способности аминокислот.
2.Провести качественные реакции на аминокислоты и белки.
3.Оформление отчета лабораторной работы.
4.Перечень вопросов для самоподготовки.
