Биометрия методичка

Двухвыборочный F-тест для дисперсий

Если значения средних выборочных в двух или нескольких выборках близки, то применение критерия Стьюдента становится затруднительным. Проверку гипотезы о принадлежности каждой из выборок к разным генеральным совокупностям можно сделать из анализа выборочных дисперсий. Для этого применяют двухвыборочный F-тест для дисперсий. Предварительно нужно убедиться в том, что в каждой выборке распределение признака близко к нормальному.

Пример. Были сформированы две группы уток одной породы по 23 единицы в каждой группе. Утки первой (контрольной) группы получали основной рацион, а утки второй (опытной) группы получали специальную кормовую добавку.

В Таблице 5.6 приведены результаты взвешивания уток на 45-е сутки. Необходимо установить достоверность различия живой массы уток 1-й и 2-й групп вследствие разных условий откорма.

Таблица 5.6 – Результаты взвешивания уток

31

Решение. Открываем новую книгу или новый рабочий лист в Ms Excel и копируем Таблицу 5.6. Сделаем предварительную статистическую обработку данных с помощью ин-

струмента Описательная статистика.

Результаты приведены на Рис. 5.2.

Рис. 5.2 – Результаты применения инструмента «Описательная статистика»

Таблицы итоговой статистики показывают, что средние выборочные значения массы в двух группах уток очень близки по значению (1872,652 г и 1901,455 г соответственно), а дисперсии отличаются почти в два раза.

Асимметрия и эксцесс в каждой группе имеют небольшие значения, что в первом приближении указывает на то, что распределение живой массы уток в каждой группе близко к нормальному.

32

Применение t-критерия Стьюдента не представляется возможным ввиду близости двух средних выборочных. Поэтому применим двухвыборочный F-тест для дисперсий. Выполняем команды Данные / Анализ данных / Двухвыборочный F-тест длядисперсий.

Появляется диалоговое окно, показанное на Рис. 5.3.

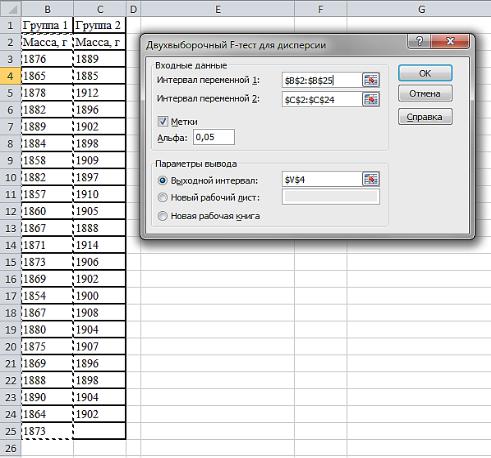
Рис. 5.3 – Диалоговое окно инструмента «Двухвыборочный F-тест для дисперсий»

Сначала в окошко «Интервал переменной 1» вводим значения живой массы уток 1-й группы (обводим курсором ячейки B2 : B25). В этой группе дисперсия больше, поэтому эти данные вводятся первыми. Потом в окошко «Интервал переменной 2» вводим значения живой массы уток 2-й группы (обводим курсором ячейки C2 : C24). В окошке «Альфа» указываем максимально допустимый уровень значимости различий «0,05». Далее указываем ячейку выходного интервала (например, V4). После этого нажимаем «ОК».

33

Результаты вычислений приведены на Рис. 5.4.

Рис. 5.4 – Двухвыборочный F-тест для дисперсии

На Рис. 5.4 обозначения «Средние» и «Дисперсия» указывают:

значения средних выборочных масс уток и отклонения для каждой из групп;

«Наблюдения» – объемы выборок;

«df» – число степеней свободы (объем выборки: –1);

«F» – фактическое значение F-критерия;

«P (F <= f) одностороннее» – реальный уровень значимости критерия;

«F критическое» – табличное значение F-критерия на уровне значимости р= 0,05.

Данные Рис. 5.4 свидетельствуют о том, что распределения живой массы уток в двух группах на 45-е сутки опыта достоверно не отличаются (уровень значимости р = 0,079926627, что больше, чем 0,05 ).

Задания Задание 1. Были проведены исследования по влиянию

органо-минерального удобрения на площадь листовой пластинки земляники садовой. Для этого были сформированы два варианта растений земляники сорта Сальса по 25 единиц в каждой группе. В стандартном варианте удобрения вносили по традиционной схеме, в опытном варианте вносили дополнительно органо-минеральное удобрение.

34

В Таблице 5.7 приведены результаты измерения листовой пластинки земляники садовой в период плодоношения.

Необходимо убедиться в достоверности различий средних значений опытного и стандартного вариантов.

Таблица 5.7 – Результаты измерений площади листовой пластинки земляники садовой

Задание 2. На свиноферме зарегистрировано 64 опороса свиноматок. При этом от каждой свиноматки получено следующее количество живых поросят (Таблица 5.8):

Таблица 5.8 – Результаты опороса свиноматок

35

Рассчитать:

1)среднюю арифметическую, размах, моду и медиану, коэффициент вариации, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение. Расчеты произвести с помощью статистических функций Microsoft Excel: СРЗНАЧ, МАКС, МИН, МЕДИАНА, МОДА.ОДН, СРОТКЛ, ДИСПА, СТАНДОТКЛОНА.

2)Рассчитать среднюю квадратическую ошибку для генеральной средней (стандартную ошибку), коэффициент Стьюдента, определить интервал для генеральной средней. Расчеты произвести с помощью статистических функций Microsoft Excel: СТАНДОТКЛОНПА, ДОВЕРИТ.НОРМ, СТЬЮДЕНТ.ОБР.

3)Рассчитать с помощью статистических функций КВАРТИЛЬ.ВКЛ и ПЕРСЕНТИЛЬ.ВКЛ 1,3 квартили и 25, 50

и70 перцентили. Рассчитать асимметрию и эксцесс. Проверить результаты спомощью статистических функций СКОС

иЭКСЦЕСС. Сделать вывод о нормальности распределения экспериментальныхданных.

Задание 3. Измерили рост 55 студенток III курса биотехнологического факультета (Таблица 5.9).

Таблица 5.9 – Рост студенток III курса биотехнологического факультета (в см)

Рассчитать:

1)среднюю арифметическую, размах, моду и медиану, коэффициент вариации, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение. Расчеты произвести с помощью статистических функций Microsoft

36

Excel: СРЗНАЧ, МАКС, МИН, МЕДИАНА, МОДА.ОДН, СРОТКЛ, ДИСПА, СТАНДОТКЛОНА.

2)Рассчитать среднюю квадратическую ошибку для генеральной средней (стандартную ошибку), коэффициент Стьюдента, определить интервал для генеральной средней. Расчеты произвести с помощью статистических функций Microsoft Excel: СТАНДОТКЛОНПА, ДОВЕРИТ.НОРМ, СТЬЮДЕНТ.ОБР.

3)Рассчитать с помощью статистических функций КВАРТИЛЬ.ВКЛ и ПЕРСЕНТИЛЬ.ВКЛ 1,3 квартили и 25, 50 и 70 перцентили. Рассчитать асимметрию и эксцесс. Проверить результаты с помощью статистических функций СКОС и ЭКСЦЕСС. Сделать вывод о нормальности распределения экспериментальных данных.

Задание 4. Взвешивание 35 взрослых кроликов дало следующие результаты (Таблица 5.10):

Таблица 5.10 – Результаты взвешивание взрослых кроликов (кг)

Рассчитать:

1)среднюю арифметическую, размах, моду и медиану, коэффициент вариации, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение. Расчеты произвести с помощью статистических функций Microsoft Excel: СРЗНАЧ, МАКС, МИН, МЕДИАНА, МОДА.ОДН, СРОТКЛ, ДИСПА, СТАНДОТКЛОНА.

2)Рассчитать среднюю квадратическую ошибку для генеральной средней (стандартную ошибку), коэффициент Стьюдента, определить интервал для генеральной средней. Расчеты произвести с помощью статистических функций Microsoft Excel: СТАНДОТКЛОНПА, ДОВЕРИТ.НОРМ, СТЬЮДЕНТ.ОБР.

37

3)Рассчитать с помощью статистических функций КВАРТИЛЬ.ВКЛ и ПЕРСЕНТИЛЬ.ВКЛ 1,3 квартили и 25, 50 и 70 перцентили. Рассчитать асимметрию и эксцесс. Проверить результаты спомощью статистических функций СКОС и ЭКСЦЕСС. Сделать вывод о нормальности распределения экспериментальныхданных.

38

Лабораторная работа № 6 Однофакторный дисперсионный анализ

Когда выборочных совокупностей, которые сравнивают между собой, много (более трех), то применение двухвыборочных t- и F-тестов попарного сравнения становится громоздким и сложным. Если известно, что различия между группами обусловлены влиянием только одного определяющего фактора (время, условия содержания, температура, доза препарата и пр.), то применяют однофакторный дисперсионный анализ (ОДА). Суть ОДА заключается в сравнении межгрупповой и внутригрупповой дисперсий. ОДА может определить достоверность и силу влияния фактора. Отметим, что перед применением ОДА нужно убедиться в том, что в каждой выборке распределение признака является близким к нормальному.

Пример. Изучали отличия в урожайности четырех сортов яровой пшеницы. Исследования проводили в пятикратной повторности. Результаты исследований приведены в Таблице 6.1.

Необходимо установить достоверность и силу влияния фактора – влияние сортовых особенностей яровой пшеницы на урожайность.

Таблица 6.1 – Урожайность сортов яровой пшеницы

Решение. Открываем новую книгу (или новый рабочий лист) в ППП Excel и копируем Таблицу 6.1. Эта таблица называется дисперсионным комплексом. Сначала проверим гипотезу о близости распределения признака – прироста живой массы поросят в каждой группе к нормальному распределению. Для этого применим инструмент Описательная статистика.

Результаты приведены на Рис. 6.1.

39

Рис. 6.1 – Результаты применения инструмента «Описательная статистика»

По значениям асимметрии и эксцесса рассчитаем коэффициентыКАи КЕпоформулам(6.1) и(6.2):

где А – асимметрия; Е – эксцесс из Рис. 6.1;

n – объем каждой выборки (n = 5).

Результаты приведены в Таблице6.2. Из данных Таблицы6.2 видно, что все значения коэффициентов меньше 3, поэтому в первом приближении принимаем гипотезу о близости распределения приростов живой массы поросят в каждой группек нормальному.

40