Лабораторная работа 3

1) S(x₃x₂x₁x₀) = x₂x₁x₀ x₃

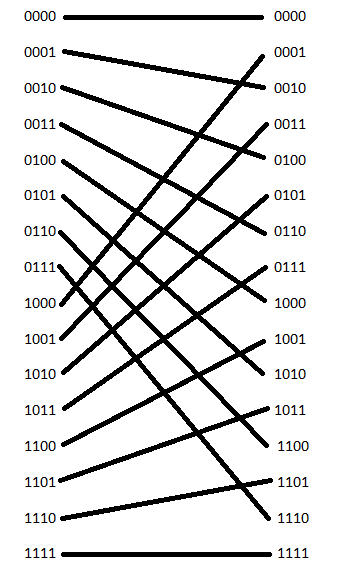
2) N = ∑2^k , где k = 0…n, n – количество уровней в дереве

N = 1 + 2 + … + 2ⁿ = 2ⁿ⁺¹ - 1

N+1 = 2ⁿ⁺¹

2ⁿ = (N+1)/2

n = log₂((N+1)/2)

D в бинарном дереве будет равно удвоенному расстоянию от узла на самом нижнем уровне до корня дерева, то есть, 2n, отсюда:

D = 2log₂((N+1)/2)

d равно 2 для корня дерева, 1 для листьев дерева и 3 для узлов, не являющихся ни листьями, ни корнем.

I = ∑2^k , где k = 1…n, n – количество уровней в дереве

I = N-1, поскольку с каждым новым уровнем в сеть добавляется 2ⁿ каналов, где n – номер добавляемого уровня

B = 1, поскольку разрез любого из двух каналов, идущих от корня дерева, разделит дерево примерно пополам.

С₁ = 2 (2 выходных канала)

С_N+1-x … C_N = 1 (1 входной канал), x = 1…2ⁿ, n – количество уровней в дереве

Для остальных узлов C_x = 3 (1 входной, 2 выходных)

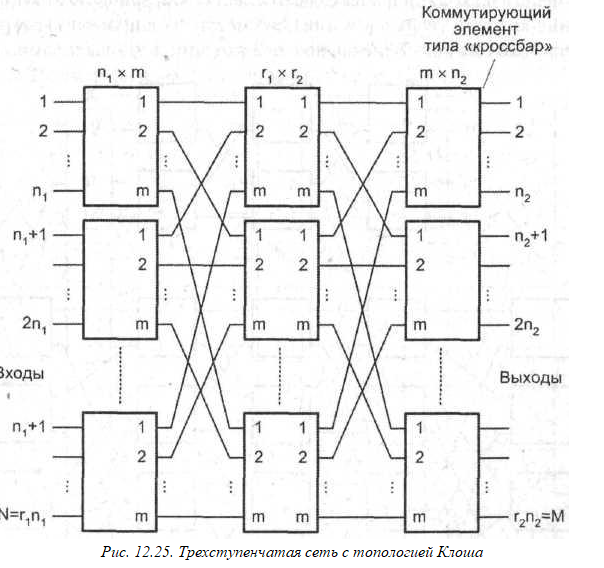
3) Примером строго неблокирующей сети может служить сеть Клоша, поскольку при выполнении условия m >= n₁ + n₂ – 1, потому что из любого входящего КЭ есть путь до исходящего КЭ через промежуточную ступень

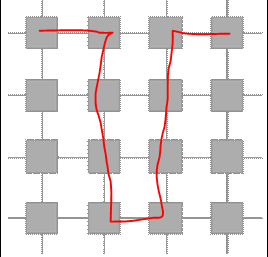
Примером неблокирующей сети в широком смысле может служить матричная сеть, поскольку в матричной сети необходимо прокладывать маршрут соединений таким образом, чтобы одни соединения не создавали блокировки для других. На рисунке приведен пример соединения, создающего блокировку для остальных пар входов и выходов.