1.4.2. Топология сети вычислительных кластеров

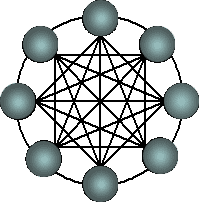
Для построения кластерной системы во многих случаях используют коммутатор (switch), через который процессоры кластера соединяются между собой. В этом случае топология сети кластера представляет собой полный граф (рис. 1.7), в соответствии с которым передача данных может быть организована между любыми двумя процессорами сети. При этом, однако, одновременность выполнения нескольких коммуникационных операций является ограниченной – в любой момент времени каждый процессор может принимать участие только в одной операции приема-передачи данных. Как результат, параллельно могут выполняться только те коммуникационные операции, в которых взаимодействующие пары процессоров не пересекаются между собой.

1.4.3. Характеристики топологии сети

В качестве основных характеристик топологии сети передачи данных наиболее широко используется следующий ряд показателей:

• диаметр – показатель, определяемый как максимальное расстояние между двумя процессорами сети (под расстоянием обычно понимается величина кратчайшего пути между процессорами). Эта величина может характеризовать максимально необходимое время для передачи данных между процессорами, поскольку время передачи обычно прямо пропорционально длине пути;

• связность (connectivity) – показатель, характеризующий наличие разных маршрутов передачи данных между процессорами сети. Конкретный вид данного показателя может быть определен, например, как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области;

• ширина бинарного деления (bisection width) – показатель, определяемый как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области одинакового размера;

• стоимость – показатель, который может быть определен, например, как общее количество линий передачи данных в многопроцессорной вычислительной системе.

Для сравнения в таблице 1 приводятся значения перечисленных показателей для различных топологий сети передачи данных.

Таблица 1.1. Характеристики топологий сети передачи данных (p – количество процессоров)

Топология	Диаметр	Ширина	Связность бисекции	Стоимость
Полный граф	1	p2/4	p–1	p(p–1)/2
Звезда	2	1	1	p–1
Полное двоичное дерево	2log((p+1)/2)	1	1	p–1
Линейка	p–1	1	1	p–1
Кольцо	[p/2]	2	2	p
Решетка N=2			2
Решетка-тор N=2			4	2p
Гиперкуб	log p	p/2	log p	(p log p)/2

Проблемы выполнения сети связи процессоров в кластерной системе

Архитектура кластерной системы (способ соединения процессоров друг с другом) в большей степени определяет ее производительность, чем тип используемых в ней процессоров. Критическим параметром, влияющим на величину производительности такой системы, является расстояние между процессорами. Так, соединив вместе 10 персональ­ных компьютеров, мы получим систему для проведения высокопроизводительных вычислений. Проблема, однако, будет состоять в поиске наиболее эффективного способа соединения стандартных средств друг с другом, поскольку при увеличении производительности каждого процессора в 10 раз производительность системы в целом в 10 раз не увеличится.

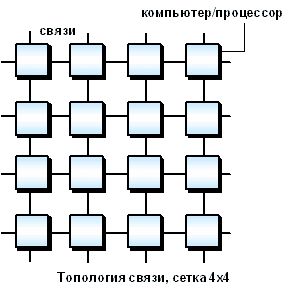
Рассмотрим для примера задачу построения симметричной 16-процессорной системы, в которой все процессоры были бы равноправны. Наиболее естественным представляется соединение в виде плоской решетки, где внешние концы используются для подсоединения внешних устройств.

Рис. 4.3. Схема соединения процессоров в виде плоской решетки

При таком типе соединения максимальное расстояние между процессорами окажется равным 6 (количество связей между процессорами, отделя­ющих самый ближний процессор от самого даль­него). Теория же показывает, что если в системе максимальное расстояние между процессорами больше 4, то такая система не может работать эффективно. Поэтому при соединении 16 процессоров друг с другом плоская схема является нецелесообразной. Для получения более компактной конфигурации необходимо решить задачу о нахождении фигуры, имеющей максимальный объем при минимальной площади поверхности. В трехмерном пространстве таким свойством обладает шар. Но поскольку нам необходимо построить узловую систему, вместо шара приходится использовать куб (если число процессоров равно 8) или гиперкуб, если число процессоров больше 8. Размерность гиперкуба будет определяться в зависимости от числа процессоров, которые необходимо соединить. Так, для соединения 16 процессоров потребуется четырехмерный гиперкуб. Для его построения следует взять обычный трехмерный куб, сдвинуть в нужном направлении и, соединив вершины, получить гиперкуб размером 4.

Рис. 4.4. Топология связи, 3-х мерный гиперкуб	Рис. 4.5. Топология связи, 4-х мерный гиперкуб
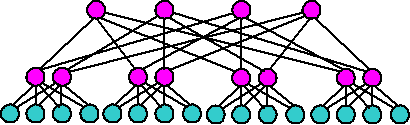
Рис. 4.6. Архитектура кольца с полной связью по хордам (Chordal Ring)		Рис. 4.7. Кластерная архитектура "Fat-tree"

Архитектура гиперкуба является второй по эффективности, но самой наглядной. Используются и другие топологии сетей связи: трехмерный тор, "кольцо", "звезда" и другие.

Рис. 4.8. Кластерная архитектура "Fat-tree" (вид сверху на предыдущую схему)

Наиболее эффективной является архитекту­ра с топологией "толстого дерева" (fat-tree). Архи­тектура "fat-tree" (hypertree) была предложена Лейзерсоном (Charles E. Leiserson) в 1985 году. Процессоры локализованы в листьях дерева, в то время как внутренние узлы дерева скомпонованы во внутреннюю сеть. Поддеревья могут общаться между собой, не затрагивая более высоких уровней сети.

Поскольку способ соединения процессоров друг с другом больше влияет на производитель­ность кластера, чем тип используемых в ней процессоров, то может оказаться более целесообразным создать систему из большего числа дешевых компьютеров, чем из меньшего числа дорогих. В кластерах, как правило, используются операционные системы, стандартные для рабочих станций, чаще всего свободно распространяемые (Linux, FreeBSD), вместе со специальными средствами поддержки параллельного программирования и балансировки нагрузки. При работе с кластерами, так же, как и с MPP-системами, используют так называемую Massive Passing Programming Paradigm – парадигму программирования с передачей данных (чаще всего – MPI). Умеренная цена подобных систем оборачивается большими накладными расходами на взаимодействие параллельных процессов между собой, что сильно сужает потенциальный класс решаемых задач.

8