Топология коммуникационных сетей мультипроцессорных систем
Топология коммуникационной сети определяет схему размещения линий связи и коммутаторов (это может быть, например, кольцо или решетка). Топологию сетей принято изображать в виде графов, в которых дуги соответствуют линиям связи, а узлы – коммутаторам. С каждым узлом в сети (или в соответствующем графе) связан определенный набор линий связи. Математики называют число линий степенью узла, инженеры – коэффициентом разветвления. Чем больше степень, тем больше вариантов маршрута и тем выше отказоустойчивость. Если каждый узел содержит k дуг и связи выполнены правильно, можно построить коммуникационную сеть так, чтобы она оставалась полносвязной, даже если повреждены k – 1 линий.
Следующая характеристика коммуникационной сети – ее диаметр. Если расстоянием между двумя узлами мы будем считать число дуг, которые нужно пройти, чтобы попасть из одного узла в другой, то диаметром графа является расстояние между двумя узлами, расположенными дальше всех друг от друга. Диаметр сети определяет самую большую задержку при передаче пакетов от одного процессора к другому или от процессора к памяти, поскольку каждая пересылка через линию связи занимает определенное время. Чем меньше диаметр, тем выше производительность. Также имеет большое значение среднее расстояние между парой узлов, поскольку от него зависит среднее время передачи пакета.
Еще одна важная характеристика коммуникационной сети – ее пропускная способность, то есть объем данных, которые она способна передавать в секунду. Наиболее полезной метрикой пропускной способности является пропускная способность сечения. Чтобы вычислить это значение, нужно мысленно разделить коммуникационную сеть на две равные (с точки зрения числа узлов) несвязанные части путем удаления ряда дуг из графа, а затем посчитать общую пропускную способность удаленных дуг. Пропускная способность сечения – это минимальная (для всех доступных вариантов) пропускная способность. Например, пропускная способность сечения, равная 800 бит/с, означает, что если между двумя частями сети много связей, общая пропускная способность в худшем случае составит только 800 бит/с. По мнению многих разработчиков, пропускная способность сечения – самая важная характеристика коммуникационной сети. Часто основная цель, которую ставят разработчики коммуникационной сети, – добиться максимальной пропускной способности сечения.
Коммуникационные сети можно характеризовать по их размерности. Размерность определяется числом возможных вариантов перехода от источника к приемнику. Если выбора нет (то есть существует только один путь от каждого источника к каждому приемнику), то сеть нульмерная. Если есть два возможных варианта (например, либо на восток, либо на запад), то сеть одномерная. Если есть две оси, и пакет может направиться на восток или на запад либо на север или на юг, то говорят, что такая сеть двухмерная, и т.д.
На рис.1 показано несколько топологий. Здесь изображены только линии связи и коммутаторы (в виде точек). Модули памяти и процессоры (они на рисунке не показаны) соединяются с коммутаторами через интерфейсы. На рис.1,а изображена нульмерная конфигурация звезда, в которой процессоры и модули памяти подключаются к внешним узлам, а переключение совершает центральный узел. Такая схема очень проста, но в большой системе центральный коммутатор окажется узким местом системы. С точки зрения отказоустойчивости это тоже очень неудачная схема, поскольку отказ одного центрального коммутатора вызывает крах всей системы.
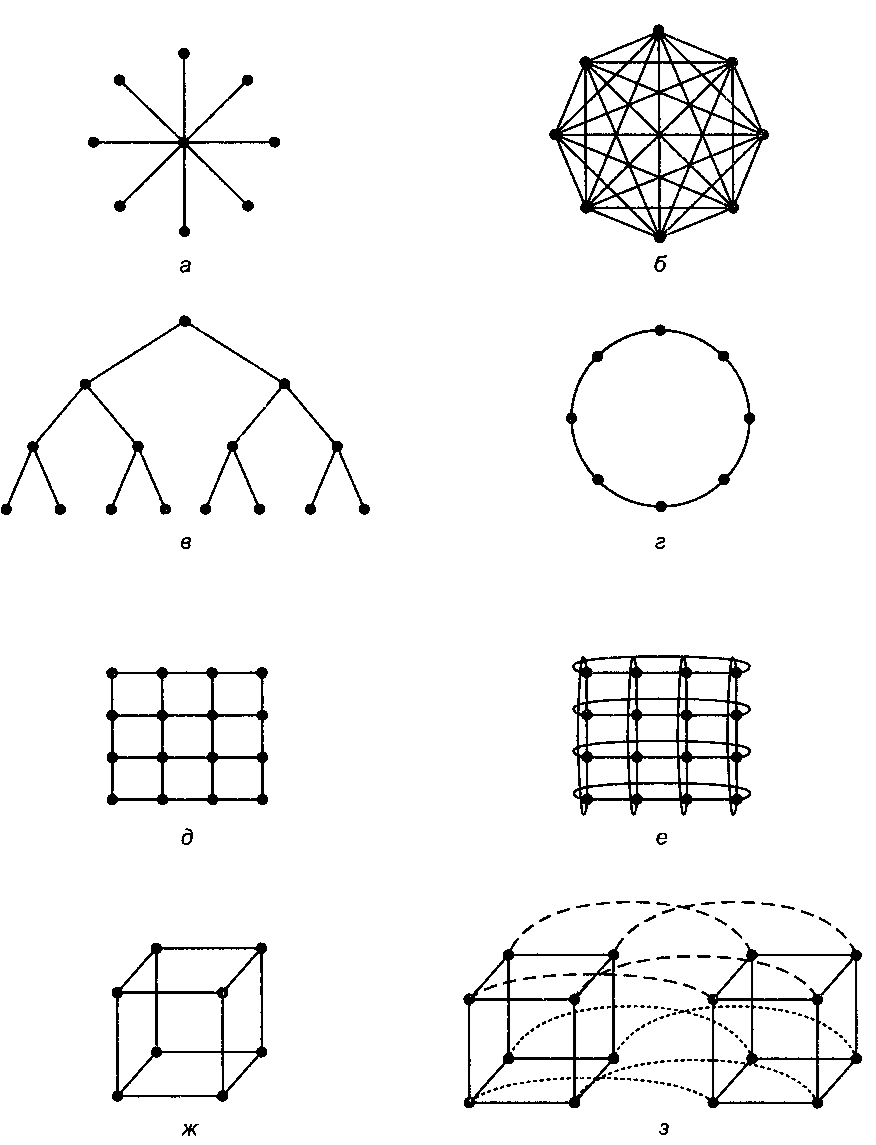
На рис.1,б изображена другая нульмерная топология – полная взаимосвязь. Здесь каждый узел непосредственно связан со всеми остальными. В такой схеме пропускная способность сечения максимальна, диаметр минимален, а отказоустойчивость очень высока (даже при утрате шести линий связи система все равно остается полносвязной). Однако для k узлов требуется k(k–1)/2 каналов, а это совершенно неприемлемо для больших значений k.
Следующая топология – дерево (рис.1,в). Здесь основная проблема состоит в том, что пропускная способность сечения равна пропускной способности линии связи. Обычно основной трафик наблюдается у верхушки дерева, поэтому верхние узлы становятся узким местом всей системы. Чтобы разрешить эту проблему, нужно увеличить пропускную способность сечения путем увеличения пропускной способности верхних линий связи. Например, самые нижние линии могут иметь пропускную способность b, следующий уровень – 2b, а каждая линия верхнего уровня – 4b. Такая схема, названная толстым деревом (fat tree), применялась в коммерческих мультикомпьютерах Thinking Machines СМ-5.
Кольцо (рис.1,г) - это одномерная топология, поскольку каждый отправленный пакет может пойти направо или налево. Решетка, или сетка (рис.1,д), – это двухмерная топология, которая применяется во многих коммерческих системах. Она отличается регулярностью и легко масштабируется в сторону увеличения, а ее диаметр составляет квадратный корень от числа узлов (то есть при масштабировании системы диаметр увеличивается незначительно). Двойной тор (рис.1,е) является разновидностью решетки, у которой края соединены. Эта топология характеризуется более высокой отказоустойчивостью и меньшим диаметром, чем обычная решетка, поскольку в ней между двумя противоположными узлами всего два хопа.
Еще одна популярная топология – трехмерный тор. Эта топология описывается трехмерной структурой, узлы которой находятся в точках (i, j, k), а все координаты являются целыми в пределах от (1, 1, 1) до (l, m, n). У каждого узла есть шесть соседей, по два вдоль каждой оси координат, а крайние узлы на противоположных краях связаны друг с другом, как и в двухмерных торах.
Куб (рис.1,ж) - это регулярная трехмерная топология. На рисунке изображен куб размером 2*2*2, но в общем случае это может быть куб размером k * k * k. На рис.1,з показан четырехмерный куб, полученный из двух трехмерных кубов, которые связаны между собой. Можно сделать пятимерный куб, соединив вместе 4 четырехмерных куба. Чтобы получить 6 измерений, нужно продублировать блок из 4 кубов и соединить соответствующие узлы и т.д. Гиперкубом называется n-мерный куб (рис.1,з). Эта топология используется во многих параллельных компьютерных архитектурах, поскольку ее диаметр линейно зависит от размерности. Другими словами, диаметр – это логарифм по основанию 2 от числа узлов, поэтому 10-мерный гиперкуб имеет 1024 узла, но диаметр равен всего 10, что дает очень незначительные задержки при передаче данных. Отметим, что решетка размером 32 х 32, которая также содержит 1024 узла, имеет диаметр 62, что более чем в шесть раз больше, чем у гиперкуба. Цена, которую приходится платить за меньший диаметр гиперкуба, - увеличение числа разветвлений и, следовательно, линий связи. Тем не менее, гиперкуб – основное решение для высокопроизводительных систем.