
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ КОРАБЛЕБУДУВАННЯ
ім. адмірала Макарова
Д.Ю. Шарейко, І.С. Білюк, О.В. Савченко, А.М. Фоменко
ПРАКТИКУМ З КУРСУ
"ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ"
частина 1
ПЕРЕДАТОЧНА ФУНКЦІЯ
Миколаїв |
9 |
УДК 681.5
Автори:
Д.Ю. Шарейко, кандидат технічних наук;
І.С. Білюк, кандидат технічних наук;
О.В. Савченко, аспірант;
А.М. Фоменко, доцент НУК.
Рецензент:
Р.А.Ставинський, к.т.н. доцент.
Шарейко Д.Ю.
Практикум з курсу "Теорія автоматичного керування" Ч.1, передаточна функція / Д.Ю. Шарейко, І.С. Білюк, О.В. Савченко, А.М. Фоменко. –
Миколаїв: НУК, 2019 – 27 с
Кафедра автоматики У практикумі наведені приклади отримання передаточних функції для
активних та пасивних чотирьохполюсників. Розглянуто алгебру передаточної функції з прикладами для отримання її для складних схем на підставі розвинення цих схем на окремі чотирьохполюсники та згортки структурної схеми. Також додаються від 18 до 24 варіантів різних задач, котрі можна використовувати як для модульного контролю так і для самостійної проробки. Практикум призначений для студентів зі спеціальності 141
«Електроенергетика, електротехніка та електромеханіка».
УДК 681.5
©Шарейко Д.Ю., Білюк І.С., Савченко О.В., Фоменко А.М.. 2019
©Національний університет кораблебудування імені адмірала Макарова, 2019
Зміст
1 Отримання передаточних функцій активних та пасивних чотирьохполюсників………………………………………………………3
1.1Приклад знаходження передаточної функції пасивного чотирьохполюсника…………………………………………………6
1.2Приклад знаходження передаточної функції активного
чотирьохполюсника…………………………………………………8 2 Алгебра передаточної функції………………………………………….15
2.1Приклад застосування алгебри передаточної функції………………………………………………………..……20
Література……………………………………………………………………27

1Отримання передаточних функцій активних та пасивних чотирьохполюсників
Після складання диференційного рівняння (д. р.) системи з урахуванням вилучення всіх проміжних координат, та формалізації цього рівняння [1-4] отримаємо наступне:
a |
d n X |
вих |
|
a |
d n-1 X |
вих |
a |
d n-2 X |
вих |
... a |
X |
|
|
|
||||||||
|
dtn |
|
dtn-1 |
|
dtn-2 |
|
|
|||||||||||||||
0 |
|
1 |
|
2 |
|
|
n |
|
|
вих |
|
|||||||||||
b |
|
|
d m Xвх |
b |
|
d m-1 Xвх |
b |
d m-2 Xвх |
... b |
|
X |
|
(1) |
|||||||||
|
|
|
|
|
|
|||||||||||||||||
0 |
|
dtm |
1 |
|
dtm-1 |
2 |
|
dtm-2 |
|
m |
|
|
вих |
|
||||||||
де a0 – an , b0 – bm , lby, динамічні коефіцієнти, що отримані в результаті формалізації.
Ліва частина рівняння відповідає внутрішнім властивостям системи, права частина – зовнішнім впливам. Враховуючи теореми диференціювання та інтегрування оригіналу з розділу математики «Операційне обчислення» отримуемо:
|
х(t) X p , |
|
|
|
|
||
x(t) |
|
X(p), |
|
|
|
|
|
|
dх(t) |
p X p c, |
|||||
|
dt |
||||||
|
|
|
|
|
|
|
|
|
d n х(t) |
pn X |
|
p |
|
c, |
|
|
|
||||||
|
dtn |
|
|
|
|
||
х(t)dt 1p X p c,
Де х(t) – орігінал, Х(р) – зображення
Перетворимо за Лапласом д. р. (1) при нульових початкових умовах, коли відсутня стала інтегрування с.
Xвх p a0 pn a1 pn 1 a2 pn 2 ... an |
|
b0 pm b1 pm 1 b2 pm 2 ... bm Xвх р |
(2) |
Xвих p |
|
b |
pm b |
pm-1 |
b |
pm-2 |
... b |
(3) |
Xвх p |
a |
pn a |
pn-1 |
a |
pn-2 |
... a |
||
|
|
0 |
1 |
|
2 |
|
m |
|
|
|
0 |
1 |
|
2 |
|
n |
|
Рівняння (3) є передаточна функція W(p) .
Передаточна функція – це відношення вихідної координати, що перетворена за Лапласом при початкових нульових умовах, до вхідної координати, що перетворена за Лапласом при початкових нульових умовах [1].
Властивості передаточної функції:
1.Передаточна функція завжди дрібно раціональна, відносно оператору р. Це стосується реальних систем: n m.
m.
2.Коефіцієнти передаточної функції є дійсні величини, тому що вони є комбінаціями реальних параметрів елементів схеми.
3.Корені характеристичного рівняння, тобто знаменника передаточної функції, завжди або комплексно спряжені з від`ємними дійсними частинами, або дійсні від`ємні.
Пропонується знаходити передаточні функції на прикладі електричних схем чотирьохполюсників. Адже будь яку електричну, електромеханічну схеми можна розвинути на окремі чотирьохполюсники. Для знаходження передаточної функції складної схеми можна використовувати алгебру передаточної функції.
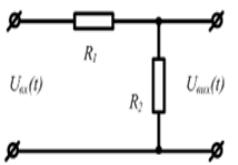
Пасивні чотирьохполюсники – це технічні елементи, що зв`язують вхідну та вихідну координати, вони не потребують залучення зовнішньої додаткової енергії (Рис.1).
Активні чотирьохполюсники – містять хоча б один елемент, що потребує присутність джерела живлення. На рисунку 2 наведений активний чотирьохполюсник на якому контакти живлення операційного підсилювача не вказані.
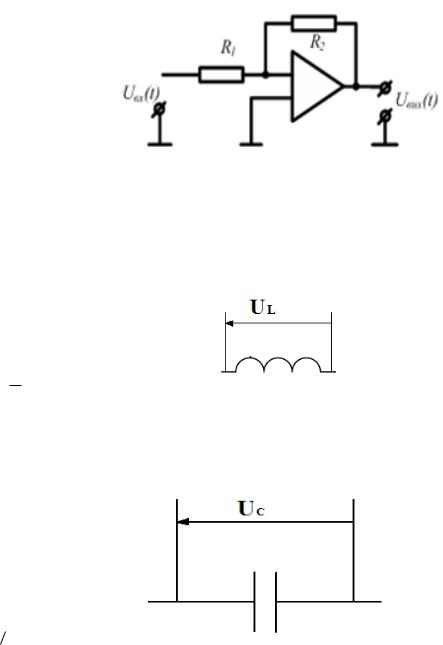
Рис. 1– Пасивний чотирьохполюсник
Рис. 2 –Активний чотирьохполюсник
При отриманні передаточної функції електричних схем необхідно враховувати наступні визначення падіння напруг на реактивних елементах
(рис.3,4).
UL=L dtdi
Рис. 3– Падіння напруги на індуктивності
Uc 1 C idt
Рис. 4– Падіння напруги на ємності
Зв`язок вхідної та вихідної координати чотирьохполюсника повинен відбуватися за допомогою фізичних параметрів схеми. Ніяких проміжних координат не може бути.
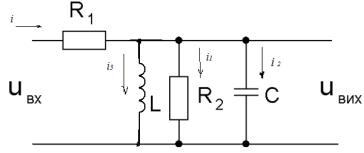
1.1 Приклад знаходження передаточної функції пасивного чотирьохполюсника
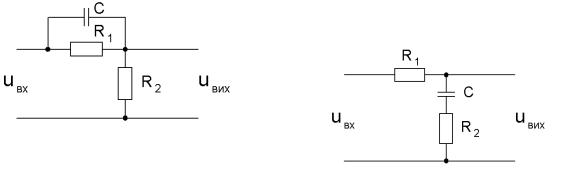
На рисунку 5 наведено пасивний чотирьохполюсник на прикладі якого буде знайдена передаточна функція.
Рис. 5 – Схема прикладу на основі пасивного чотирьохполюсника
|
|
|
i =i1 +i2 +i3. |
|
|
|
|
(4) |
||||||||
|
|
|
i =(Uвх –Uвих)/R1. |
|
|
(5) |
||||||||||
|
U |
|
|
|
|
1 |
i2 dt |
; i |
|
c dUвих . |
(6) |
|||||
|
вих |
|
|
|
||||||||||||
|
|
|
|
С |
|
|
|
2 |
|
|
dt |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U |
вих |
L |
di3 |
; |
i |
|
|
1 |
U |
|
dt . |
(7) |
||||
|
|
|
|
|
|
|||||||||||
|
|
|
dt |
|
3 |
|
L |
|
вих |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
Підставимо рівняня 5,6,7 у 4.
Uвх - Uвих |
|
Uвих |
c dUвих |
1 |
U |
|
dt . |
|
|
|
вих |
||||
R1 |
R2 |
dt |
L |
|
|||
|
|
|
|||||
Враховуючи, що передаточну функцію отримують нульових умовах, позбудемося інтегралу у рівнянні диференціювання.
(8)
при початкових 8 за рахунок
1 |
|
dUвх |
|
1 |
|
dUвих |
|
1 dUвих |
c d 2Uвих |
1 |
Uвих . (9) |
|||
|
|
|
|
|
|
|
|
|
||||||
R1 dt |
R1 dt |
R2 dt |
dt2 |
L |
|
|||||||||
Застосовуємо разом два етапи формалізації диференційного рівняння (9), а саме: перший – розділення зміняних, ліворуч розташовуємо всі вихідні координати з їх похідними, праворуч вхідні координати з їх похідними; другий – розташування координат за порядком більшості похідних.
c d 2Uвих |
R1 R2 |
|
dUвих |
|
1 |
Uвих |
1 |
|
dUвх |
. |
(10) |
|
|
|
|
|
|||||||
dt2 |
R1R2 dt |
L |
R1 dt |
|
|||||||
Третій етап формалізації – позбуваємося коефіцієнта, який знаходиться біля нульової похідної вихідної координати Uвих .
LC d 2Uвих |
L |
|
R1 R2 |
|
dUвих |
Uвих |
L |
|
dUвх |
. |
(11) |
|
|
|
|
|
|||||||
dt2 |
R1 R2 |
|
dt |
R1 dt |
|
||||||
Четвертий етап формалізації д.р. – заміна фізичних параметрів |
|||||||||||
динамічними коефіцієнтами. |
|
|
|
|
|
|
|
|
|||
T1 = L/R1 [c]; T2 = CR1 [c]; k = (R1 + R2 )/ R2.
Характерно, що наприкінці формалізації д.р. розмірності правої його частині має відповідати розмірність лівої частини. Отже маємо:
T 1T 2 d 2Uвих T 1k |
dUвих |
|
Uвих T 1 |
dUвх |
. |
(12) |
|
|
|||||
dt2 |
dt |
|
dt |
|
||
Перетворюємо диференційне рівняння 12 за Лапласом при початкових нульових умовах враховуючи теорему диференціювання оригіналу.
(T1 T2p2+ T1kp +1)Uвих(p) = T1p Uвх(p).
Нарешті знаходимо передаточну функцію:
W ( p) |
Uвих(p) |
|
T1p |
|
|
|
. |
||
U |
|
|||
|
вх(p) |
|
T1T2p2 T1kp 1 |
|
|
|
|
||
1.2 Приклад знаходження передаточної функції активного чотирьохполюсника
На рисунку 6 наведено активний чотирьохполюсник на прикладі якого буде знайдена передаточна функція.
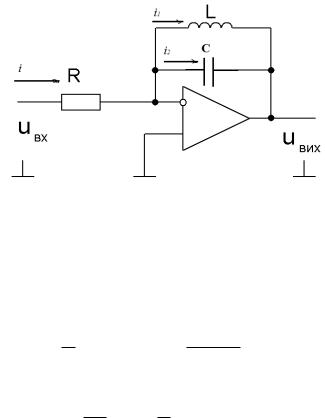
Рис. 6 – Схема прикладу на основі активного чотирьохполюсника
i =i1 +i2.
i =Uвх /R.
Uвих С1 i2 dt ; i2 c dUdtвих .
Uвих L ddti1 ; i1 L1 Uвихdt .
Підставимо рівняня 16,15,14 у 13.
Uвх |
c dUвих |
1 |
U |
|
dt . |
|
|
вих |
|||
R |
dt |
L |
|
||
|
|
|
|||
(13)
(14)
(15)
(16)
(17)
Позбудемося інтегралу аналогічно рівнянню 9, а також аналогічно проведемо два перших етапи формалізації.
|
1 |
|
dUвх |
c d 2Uвих |
1 |
Uвих . |
(18) |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
R dt |
|
dt2 |
|
L |
|
|
|
|
|
|
|
|
|
||||||
|
c d 2Uвих |
|
1 |
Uвих |
|
|
1 |
|
|
dUвх |
. |
|
(19) |
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dt2 |
|
L |
|
|
R |
|
|
dt |
|
||||||||
Позбуваємося коефіцієнта, який знаходиться біля нульової похідної |
||||||||||||||||||||
вихідної координати Uвих . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
d 2U |
вих Uвих |
|
|
L dUвх |
|
||||||||||
|
|
|
LC |
|
|
|
|
|
. |
(20) |
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
dt2 |
|
|
|
|
|
|
R1 dt |
|
|||||||
Заміняємо фізичні параметри динамічними коефіцієнтами.
T1 = L/R1 [c]; T2 = CR1 [c].
|
d 2U |
dUвх |
|
|
|
T1T 2 |
вих |
Uвих T1 |
|
. |
(21) |
|
|
||||
|
dt2 |
dt |
|
|
|
Перетворюємо диференційне рівняння 21 за Лапласом при початкових нульових умовах враховуючи теорему диференціювання оригіналу.
(T1 T2p2+ 1)Uвих(p) = T1p Uвх(p).
Знаходимо передаточну функцію:
W ( p) |
Uвих(p) |
|
T1p |
|
|
|
. |
||
U |
|
|||
|
вх(p) |
|
T1T2p2 1 |
|
|
|
|
||
В таблиці 1 наведені початкові умови 18 варіантів пасивних та активних чотирьохполюсників для знаходження передаточної функції.
Таблиця 1 – Варианта для самостійної роботи
Вариант №1 |
|
Вариант №2 |
|
Скласти диференціальне |
рівняння, |
Скласти диференціальне |
рівняння, |
формалізувати його та |
отримати |
формалізувати його та |
отримати |
передаточну функцію. |
|
передаточну функцію. |
|
|
|
|
|
|
|
|
|
