4.3 Мостовые измерительные схемы с логометрами.

Измерительную цепь с мостовой схемой и логометром представлена на рисунке(рис.6).

где: R₁, R₂, R₃, R_X — сопротивления плеч моста, причем последнее плечо — измерительное; R_P — сопротивление рамок логометра, R₅—сопротивление полудиагонали.

Отклонение подвижной системы логометра является функцией отношения сила токов в рамках, т.е.

.

Но отношение сил токов зависит от параметров схемы

или, если положить R₁=R₃,

. (21)

По формуле (21) при заданных значениях сопротивлений моста можно найти отношения сил токов в рамках логометра, а следовательно, и угол  отклонения подвижной системы.

В приборах с логометрическими указателями сопротивление полудиагонали R₅ обычно выбирают из условий компенсации температурных погрешностей, выз­ванных влиянием температуры T окружающей среды на рамки логометра. Сопротивление R₅ в этом случае выполняется из двух частей: R₅=R₅^’+R_T первое из которых с нулевым температурным коэффициентом, а второе — с положитель­ным температурным коэффициентом, например, медное.

Выберем величину сопротивления R_T из условия независимости отношения токов (21) от температуры T окружающей среды.

Положим, что

,

где а — температурный коэффициент сопротивлений.

Подставляя значения R_P и R_T в (21) и считая, что остальные сопротивле­ния не зависят от температуры окружающей среды, получим

, (22)

где

(23)

Если параметры моста выбрать из условия

, (24)

то отношение токов не будет зависеть от температуры T окружающей среды. В самом деле, исключая, например, B₁ из формулы (22), при помощи (24) получим

. (25)

Подставляя значения A₁, A₂, B₁, B₂ в (24), найдем

. (26)

Отсюда следует, что полная температурная компенсация, т. е. точное удовлетворение условию (24), возможна только тогда, когда сумма сопротивлений R₂+R_X постоянна, т. е. когда сопротивления R₂и R_X меняются взаимно.

В схеме двойного моста (рис.7, б) рамки логометра с одной стороны соединяются вместе, а с другой — через сопротивление R₅.

Если условно считать, что одна из рамок отсутствует, то для второй рамки при условиях R₁=R₃ и R₂=R_X мост оказывается разбалансированным (вслед­ствие того, что R₅0) в одну сторону, а для первой рамки при отсутствии второй — в другую сторону. Это обстоятельство позволяет повысить чувствительность измерительной схемы.

Полученные здесь зависимости для мостов постоянного тока целиком спра­ведливы для мостов переменного тока, состоящих из чисто активных сопротивлений. Эти зависимости справедливы также в общем случае, если в полученных выражениях активные сопротивления заменить полными сопротивлениями.

4.4 Измерительные схемы статического уравновешивания.

Измерительные цепи со статическим уравновешиванием выполняются в виде компенсационных схем с обратной связью (рис.7).

Измеряемая величина х преобразуется с помощью первичного преобразователя ПП в величину F_X, уравновешиваемую величиной F_Y, получаемой от обратного преобразователя ОП. Входной величиной обратного преобразователя является выходная величина I, формируемая в прямой цепи, состоящей из преобразователя неравновесия ПН, модулятора М, усилителя Ус и демодулятора ДМ. На вход преобразователя ПН поступает сигнал рассогласования F=F_X-F_Y.

Измерительная цепь статического уравновешивания состоит из прямой цепи с преобразованием FI и коэффициентом преобразования (передачи) К и цепи обратной связи с преобразованием IF и коэффициентом преобразования (передачи) .

Важной особенностью цепей уравновешивания является обратный преобразователь, который выполняет функцию преобразования выходной величины I в сигнал F_Y, однородный с сигналом F_X (напряжение — напряжение, сила тока — сила тока, сила — сила, момент—момент).

Из схемы (см. рис.8) видно, что К=I/F; =F_Y/I; F_Y/F=K — глубина уравновешивания; F/F_X= — относительное неравновесие; F_Y/F_X=λ — относительная глубина уравновешивания.

Пользуясь этими обозначениями, можем написать

Чувствительность измерительной цепи уравновешивания

. (27)

Отсюда следует, что чувствительность цепи уравновешивания, в 1 + K раз меньше чувствительности K прямой цепи. Уменьшение чувствительности окупается тем, что в такое же число раз уменьшается погрешность преобразования F_XI.

Погрешность измерительной цепи складывается из мультипликативной составляющей _S, обусловленной изменением чувствительности S, и аддитивной составляющей _a, возникающей в цепях K и . Для получения мультипликативной погрешности найдем связь между приращениями чувствительностей S, K и , воспользовавшись выражением (27):

Разделив последнее выражение на (27), получим

,

или, наконец,

, (28)

где .

Аддитивная погрешность (рассматриваем случайную составляющую) цепей К и , обусловленная шумами, дрейфом, наводками и нестабильностью и приведенная по входу измерительной цепи, будет

, (29)

где _K и _ абсолютные погрешности цепей K и .

Результирующая погрешность равна сумме аддитивной и мультипликативной погрешностей:

. (30)

Рассматриваем только случайные погрешности. Обычно составляющие _K, _, _K и _ не коррелированы между собой, поэтому

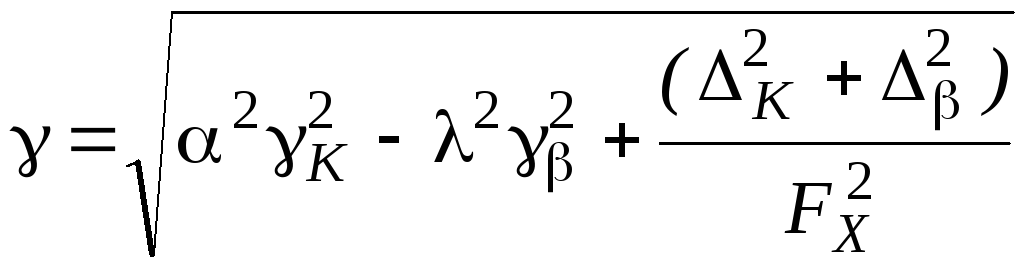
или, так как =F/F, то

. (31)

Отсюда следует, что при повышении глубины уравновешивания K величины  и λ будут соответственно α0 и λ 1, поэтому погрешности _K, _K и _ измерительной цепи уравновешивания уменьшаются в =1/(1+K) раз, тогда как мультипликативная погрешность цепи обратной связи (обратного преобразователя) _ остается неизменной. Для повышения точности измерительной цепи необходимо уменьшать _, т. е. выбирать ОП с высокостабильными параметрами. Заметим, что уменьшение погрешностей _K, _ и _K за счет обратного преобразователя в =1/(1+K) раз приводит к такому же уменьшению чувствительности S измерительной цепи статического уравновешивания.

При статическом уравновешивании для поддержания определенного значения выходной величины I необходимо на вход цепи К подавать сигнал рассогласования F=F_X-F_Y. Поскольку F=F_X и =1/(1+K), то величина F составляет постоянную часть от F_х и может быть учтена при градуировке. Приборы, содержащие измерительные цепи статического уравновешивания, имеют широкий диапазон измерения, достигающий D=10⁶. Приборы этого типа имеют большое быстродействие. Однако погрешности их вследствие того, что указатель не охвачен обратной связью, не всегда достаточно малы. При большой глубине обратной связи в приборе возможно нарушение устойчивости.

Для оценки динамических характеристик измерительных цепей статического уравновешивания следует рассматривать передаточную функцию

, (32)

где k₁(p) и k₂(p) —коэффициенты передачи первичного преобразования и указателя.