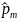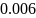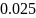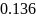- •1. По заданной функции корреляции исходного сообщения:
- •4. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе l-ичного дискретного канала связи(дкс):
- •6. Полагая, что для передачи икм сигнала по непрерывному каналу связи нкс используется гармонический переносчик:
- •График нормированного спектра сигнала дискретной модуляции
- •График фпв суммы сигнала и шума
- •8. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:
- •9. Рассматривая отклик детектора пру как случайный дискретный сигнал на выходе l-ичного дкс:
- •Закон распределения вероятностей отклика декодера
- •10. Полагая фнч на выходе цап приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:
- •Список использованной литературы.
9. Рассматривая отклик детектора пру как случайный дискретный сигнал на выходе l-ичного дкс:
а) рассчитать распределение вероятностей дискретного сигнала на выходе детектора, скорость передачи информации по L- ичному ДКС, относительные потери в скорости передачи информации по L- ичному ДКС;
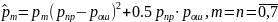 ,
где
,
где
 вероятность ошибки в двоичном симметричном
ДКС;
вероятность ошибки в двоичном симметричном
ДКС;
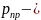 вероятность
правильного приема двоичного символа,
вероятность
правильного приема двоичного символа,
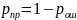
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
Для определения скорости передачи
информации
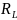 по
L — ичному ДКС воспользуемся соотношением:
по
L — ичному ДКС воспользуемся соотношением:
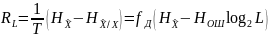
Энтропия ошибочных решений:

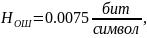
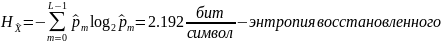
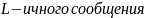 .
.

Зная производительность
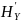 L — ичного источника(скорость ввода
информации в ДКС) и скорость передаваемой
по ДКС информации
находим
величину относительных потерь в скорости:
L — ичного источника(скорость ввода
информации в ДКС) и скорость передаваемой
по ДКС информации
находим
величину относительных потерь в скорости:
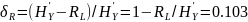
б) построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.
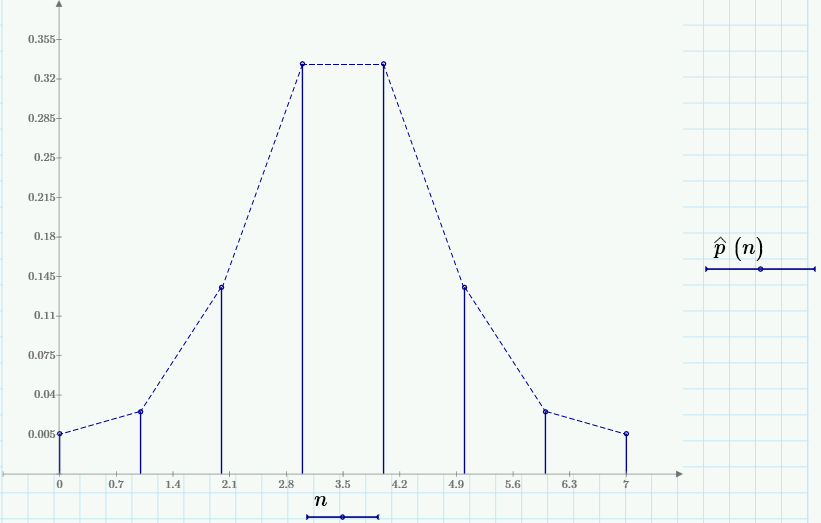
Закон распределения вероятностей отклика декодера
10. Полагая фнч на выходе цап приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:
а) рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП) суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП);
Дисперсия случайных импульсов шума передачи на выходе интерполятора ЦАП определяется:
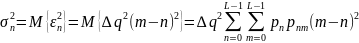
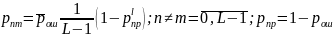
Где
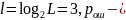 вероятность
ошибки в двоичном симметричном ДКС.
вероятность
ошибки в двоичном симметричном ДКС.
Найдем СКПП:

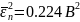
В
виду того, что погрешность фильтрации
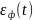 шум квантования
шум квантования
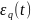 и шум передачи
и шум передачи
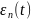 - независимые случайные процессы, то
суммарная СКП восстановления непрерывного
сообщения
- независимые случайные процессы, то
суммарная СКП восстановления непрерывного
сообщения
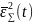 будет равна сумме СКП указанных
процессов:
будет равна сумме СКП указанных
процессов:
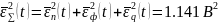
Тогда относительная суммарная СКП восстановленного сообщения, очевидно будет равна:
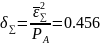
11. В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления.
Относительная суммарная СКП восстановленного сообщения, очевидно будет равна:
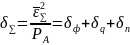
Не трудно показать, что относительные
СКП фильтрации
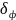 ,
квантования
,
квантования
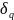 и передачи
и передачи
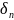 зависят от энергетической ширины спектра
сообщения
зависят от энергетической ширины спектра
сообщения
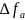 различным образом:
различным образом:
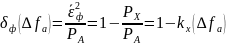
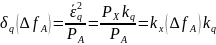

Где
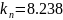 ;
;
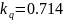

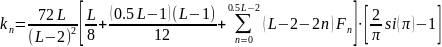
Где
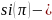 интегральный
синус:
интегральный
синус:
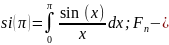 интегральный закон распределения
интегральный закон распределения
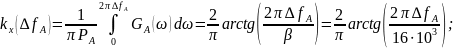
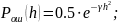
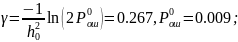

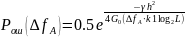
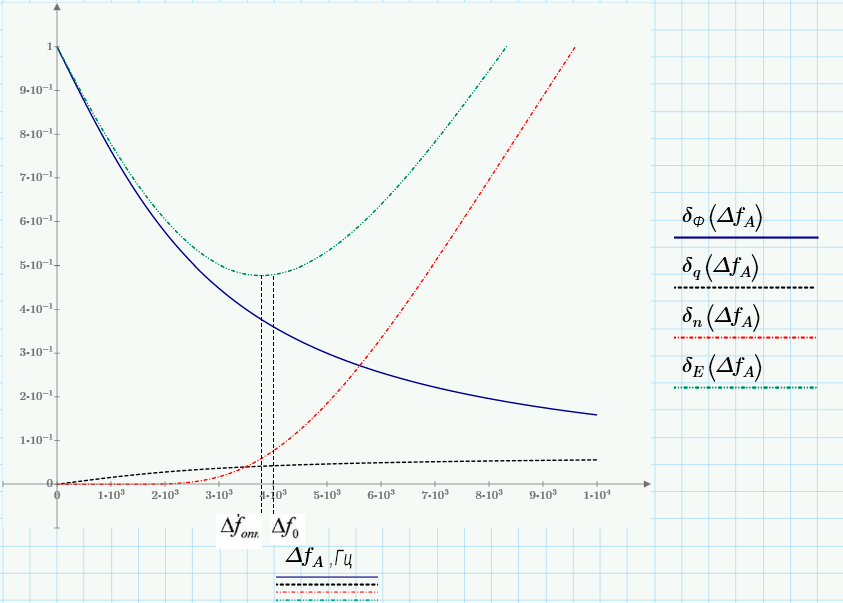
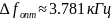
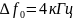
Суммарная величина относительной СКП имеет минимум при оптимально выбранной энергетической ширине спектра исходного сообщения.
Список использованной литературы.
1.В.Г.Санников-Методические рекомендации по выполнению курсовой работы-М.:1996.
2.А.Г.Зюко, Д.Д.Кловский. ТЭС:Учебник для вузов - М.:Радио и связь.1998
3.Конспект лекций.