
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение
высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра Информатики
Лабораторная работа №20а
по дисциплине «Общая теория связи»
по теме:
«Эффективное кодирование»
Вариант 1
Выполнили: студенты группы БИН220*
*
Проверила:
Доцент Кудряшова А.Ю.
Москва 2024
1. Задан дискретный источник двоичных сообщений, который производит слова, состоящие из двух букв А и М. Всего возможно четыре различных сообщения, слова : АА. AM, МА, ММ. Рассчитайте вероятность каждого слова р(АА), р(АМ), р(МА), р(ММ), если заданы (см. таблицу А) безусловные вероятности р(А), р(М) и условные вероятности. (р(А/М) - вероятность буквы A, если первой в слове была буква М; остальные обозначения аналогичны).
2.Рассчитайте энтропию источника Н и его избыточность R.
3.Закодируйте слова четверичным кодом и рассчитайте его энтропию и избыточность.
4.Закодируйте четыре слова безызбыточным кодом с префиксными свойствами, построив кодовое дерево. Рассчитайте энтропию нового двоичного кода, его избыточность и среднюю длину кодовой комбинации.
5.Запишите выражения, соответствующие передаче нуля и единицы с помощью двоичной фазовой модуляции. Запишите выражения, соответствующие передаче различных комбинаций из двух символов, «дибитов», с помощью четырехпозиционной ФМ. Нарисуйте временные диаграммы сигналов двоичной и четырехпозиционной ФМ.
Определите максимальное значение энтропии для m=2 и m=4.
Таблица А.


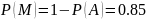
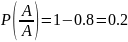
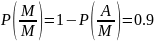
1.Рассчитаем вероятность каждого слова p(АА), p(AM), p(MA) и p(MM).

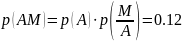
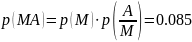
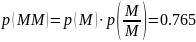
2.Рассчитаем энтропию источника H и его избыточность R
Энтропия:
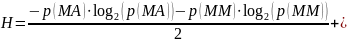

Избыточность:
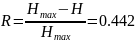

Закодируем слова четверичным кодом и рассчитаем его энтропию и избыточность
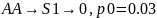
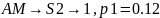
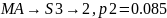

Вычислить энтропию источника:
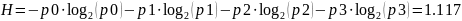
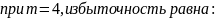
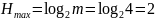
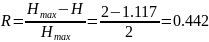
4.Закодируем четыре слова безызбыточным кодом с префиксными свойствами, построив кодовое дерево, а также рассчитаем энтропию нового двоичного кода, его избыточность и среднюю длину кодовой комбинации.
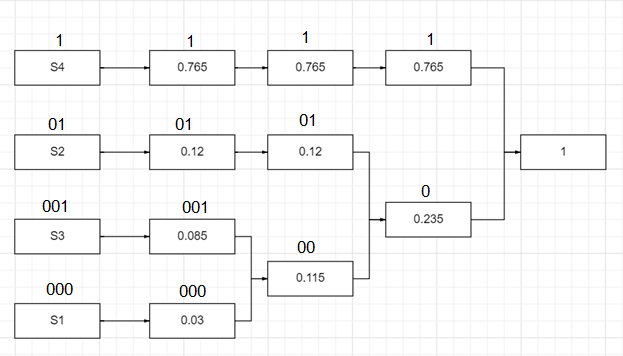
Рис.1
Закодируем исходные сообщения новым кодом. Для нашего примера получим следующие комбинации.
S4 – 1. S2 – 01. S3 – 001. S1 – 000
Энтропия нового двоичного кода рассчитывается следующим образом. Пусть слова исходного источника S1, S2, S3. S4 имеют вероятности и закодированы как в нашем примере. Из 100 среднестатистических сообщений будем иметь S1 - 3 сообщения; S2 – 12 сообщений; S3 - 9 сообщений; S4 - 76 сообщений. В соответствии с новым кодом имеем:
S1 - 3 сообщения т.e 9 символов “0”;
S2 - 12 сообщений т.e 12 символов “0” и 12 символов “1”;
S3 - 9 сообщений т.e 18 символов “0” и 9 символов “1”;
S4 - 76 сообщения т.e 76 символов “1”;
Таким образом среднестатистические сообщений содержат:
символов 0: 9 +12 + 18 = 39
символов 1: 76 + 9 + 12 = 97
Вероятность появления 0 равна: P0 = N0/(N0+N1) = 0.287
Вероятность появления 1 равна: P0 = N1/(N0+N1) = 0.713
Вычислим значение энтропии H:

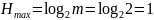

Вычислим
среднюю длину кодовой комбинации
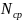

5.Запишите выражения, соответствующие передачу нуля и единицы с помощью двоичной фазовой модуляции. Запишите выражения, соответствующие передаче различных комбинаций из двух символов, «дибитов», с помощью четырехпозиционной ФМ. Нарисуйте временные диаграммы сигналов двоичной и четырех позиционной ФМ
Выражения, соответствующие передаче нуля и единицы с помощью ДФМ.
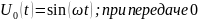
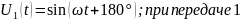
Выражения, соответствующие передаче различных из двух символов, «дибитов», с помощью четырехпозиционной ФМ.
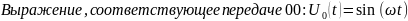
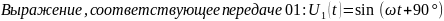


Временные диаграммы:

Рис.2
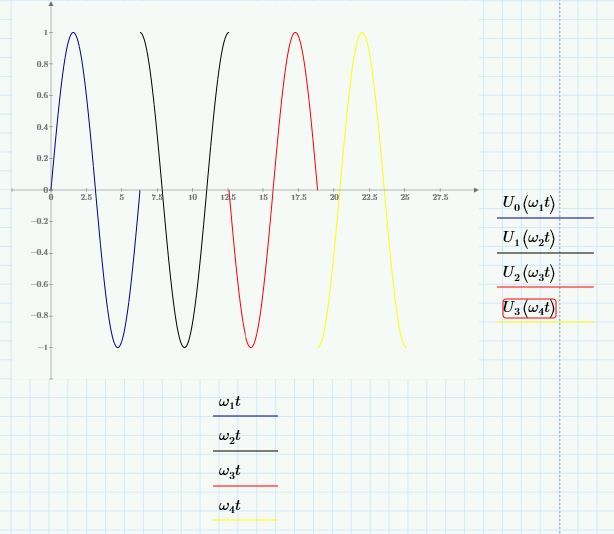
Рис.3
