
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение
высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра Информатики
Лабораторная работа №3
по дисциплине «Численные методы»
по теме:
«Аппроксимация функций»
Вариант 4
Выполнил: студент группы БИН220*
*
Проверил:
Старший преподаватель
Юсков Игорь Олегович
Москва 2024
1.Задание
Выбрать индивидуальное задание из табл. 3-1 и табл. 3-2 для решения задачи аппроксимации методом наименьших квадратов: значения функции табл. 2-2 в узлах, указанных в табл. 2-1.
Выполнить линейную аппроксимацию:
составить систему нормальных уравнений и решить её;
вычислить значения аппроксимирующих функций в узловых точках и сравнить их со значениями исходной функции;
Вычислить среднеквадратичную погрешность (СКО).
С использованием математического пакета получить аппрокси-мирующие полиномы МНК 1, 2, 3, 4, 5 степеней и соответствующие СКО. Построить графики полученных полиномов.
Проанализировать результаты.
Индивидуальный вариант
-
N варианта
Функция из табл. 3-2
Номера узлов из табл. 3-2
3
F1
4,6,8,10,12,14
-
 -номер
узла
-номер
узла


4
-1.2
0,88
2,44
6
-1.0
1,266
2,366
8
-0.8
0,286
1,006
10
-0.6
-1,06
-0,64
12
-0.4
-1,406
-1,206
14
-0.2
-0,386
-0,326
Выполнение задания
Задание для решения задачи аппроксимации
Для решения задачи аппроксимации методом наименьших квадратов выберем функцию y(x), заданную следующей таблицей:
-
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2

-0,386
-1,406
-1,06
0,286
1,266
0,88
2.Линейная аппроксимация:
Вычислим и запишем в табл. 3-3 элементы матрицы Грамма и столбец свободных членов:
-

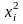
0
-0.2
-0,386
0.077
0.04
1
-0.4
-1,406
0.562
0.16
2
-0.6
-1,06
0.636
0.36
3
-0.8
0,286
-0.229
0.64
4
-1.0
1,266
-1.266
1
5
-1.2
0,88
-1.056
1.44

-4.2
-0.42
-1.276
3.64
4.табл. 3-3
Составим системы нормальных уравнений: для линейной функции P1(x) = А0+А1*x система нормальных уравнений примет вид (линейная аппроксимация):
6*А0-4.2*А1 = -0.42
-4.2*А0+3.64А1 = -1.276
решить систему уравнений: получим коэффициенты А0 = -1.64 и А1 = -2.243, тогда полином первой степени будет таким: P1(x) = -1.64-2.242*x
-
-0.4
-0.6
-0.8
-1.0
-1.2
-1,406
-1,06
0,286
1,266
0,88

-0.743
-0.294
0.154
0.603
1.051

-0.663
-0.766
0.132
0.663
-0.171
Рассчитаем
СКО:

3.Аппроксимация с помощью математического пакета
Осуществить аппроксимацию таблично заданной функции многочленом 1, 2, 3, 4 и 5-й степени.
В этом примере рассмотрено использование функции linfit(x,y,f), где x,y- соответственно векторы значений аргументов и функции, а f – символьный вектор базисных функций. Использование этой функции позволяет определить вектор коэффициентов аппроксимации методом наименьших квадратов и далее невязку - среднеквадратическую погрешность приближения исходных точек к аппроксимирующей функции (сkо). Степень аппроксимирующего многочлена задается при описании символьного вектора f. В примере представлена аппроксимация таблично заданной функции многочленом 1, 2, 3, 4, 5-й степени, . Вектор s представляет собой набор аппроксимирующих коэффициентов, что позволяет получить аппроксимирующую функцию в явном виде.
Следует построить графики для полиномов 1, 2 и 5 степени.
П роанализировать
изменение СКО в зависимости от степени
полинома.
роанализировать
изменение СКО в зависимости от степени
полинома.
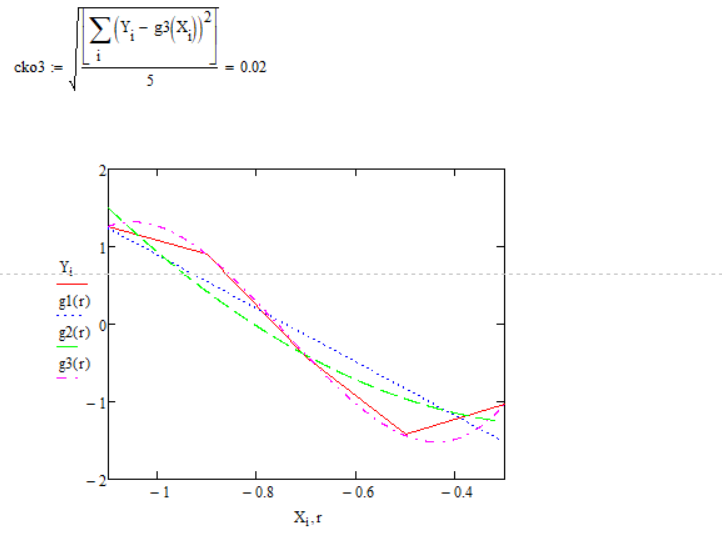
Вывод: Среднеквадратическая погрешность аппроксимации функции полиномом n-ой степени на заданном интервале зависит от свойств функции и распределения узлов интерполяции
В частности, если функция является достаточно гладкой и узлы интерполяции равномерно распределены на заданном интервале, то среднеквадратическая погрешность может быть близка к нулю при увеличении степени полинома. Однако, если функция имеет разрывы или особенности, то даже высокостепенный полином может не дать достаточно точного приближения.
Таким образом, среднеквадратическая погрешность аппроксимации полиномом 5-ой степени зависит от свойств функции и распределения узлов интерполяции, и не всегда бывает близка к нулю. В общем случае необходимо оценивать погрешность для конкретной функции и распределения узлов интерполяции.
