
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение
высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра Информатики
Лабораторная работа №2
по дисциплине «Численные методы»
по теме:
«Интерполяция функций»
Вариант 4
Выполнил: студент группы БИН220*
*
Проверил:
Старший преподаватель
Юсков Игорь Олегович
Москва 2024
I. ЗАДАНИЕ
Общее задание к работе
1. Выбрать индивидуальное задание из табл.:
точку интерполяции x = a для интерполяции многочленом Ньютона;
точку интерполяции x = b для интерполяции многочленом Лагранжа;
2. Для интерполяции в точке x = a выбрать из таблицы с интерполируемой функцией 4 подходящих узла для построения многочленов 1, 2 и 3-ей степени.
3. Перенумеровать узлы интерполяции для каждого из методов
интерполяции. Занести перенумерованные узлы в таблицы.
4. Выполнить вручную интерполяцию по заданной формуле заданной точке
x = a или x = b многочленами 1–й, 2–й и 3–й степени:
заполнить таблицу конечных разностей (для интерполяционной формулы Ньютона);
записать интерполяционные формулы для 1, 2 и 3-ей степени многочлена;
выполнить расчеты по интерполяционным формулам для каждой степени многочлена; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
занести полученные результаты в таблицу; для многочленов 1–й и 2–й степени вычислить и занести в таблицы и оценки погрешности интерполяции: модули разности между текущим Pk(x) (Lk(x)) и следующим Pk+1(x) (Lk+1(x))
значением многочлена.
5. Решить задачу интерполяции в точке с точностью 0.0001 на компьютере.
6. Объяснить полученные результаты и сделать выводы.
Индивидуальный вариант задания
-
№ вар
Вид интерполяционного многочлена
Мн-н
Ньютона
Мн-н
Лагранжа
Многочлен
Ньютона
Многочлен Лагранжа
x=a
x=b
4
0.21
0.58
На компьютере
Ручной расчёт
Рисунок 1 – Индивидуальный вариант №1
II. ВЫПОЛНЕНИЕ РАБОТЫ
1. Точка интерполяции для формулы Лагранжа b = 0.43.
Выбор и перенумерация узлов.
Для ручной интерполяции в точке x = b = 0.58 по формуле Лагранжа выбираем из таблицы 4 узла так, чтобы точка b = 0.58 оказалась в центре отрезка интерполяции: узлы с номерами с 9 по 12.
Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке с заданной точностью добавлять узлы симметрично относительно точки x.
№ узла |
Значение аргумента xi |
Значение функции yi |
9 |
0.5 |
-3.3250 |
10 |
0.55 |
-3.1385 |
11 |
0.6 |
-2.9280 |
12 |
0.65 |
-2.6920 |
Перенумеруем узлы интерполяции симметрично относительно точки х = b для использования их в интерполяционных формулах и занесем в таблицу вида:
k |
0 |
1 |
2 |
3 |
Xk |
0.55 |
0.6 |
0.5 |
0.65 |
Yk |
-3.1385 |
-2.9280 |
-3.3250 |
-2.6920 |
Ручной расчет по формуле Лагранжа.
Запишем интерполяционные многочлены Лагранжа 1–й, 2–й и 3–й
степени и вычислим их значения в точке x = b = 0.58:

Занесем результаты в таблицу и вычислим оценки погрешности
полученных значений для многочленов 1–й и 2–й степени:
Степень многочлена № |
|
Погрешность |
1 |
|
0.003 |
2 |
|
0 |
3 |
|
- |
Выражения для многочленов:
L1 = 4.21x – 5.454
L2=
![]()
L![]() 3
=
3
=
Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в т. а. Оценку погрешности проведём в соответствии с неравенством:
![]()
Можно утверждать, что разность между точным значением функции и
значением функции в т. x = 0.58 после 3-х итераций не превышает 0.001.
2. Точка интерполяции для формулы Ньютона a = 0.21.
Выбор и перенумерация узлов.
Для ручной интерполяции в точке x = a = 0.21 по 1 формуле Ньютона
выбираем 4 узла из таблицы так, чтобы точка a = 0.21 оказалась между
узлами с номерами с 0 по 1 и добавляем узлы вправо:
№ узла |
Значение аргумента xi |
Значение функции yi |
3 |
0.2 |
-4.0240 |
4 |
0.25 |
-3.9500 |
5 |
0.3 |
-3.8610 |
6 |
0.35 |
-3.7555 |
Занесем в более удобную таблицу:
k |
0 |
1 |
2 |
3 |
Xk |
0.2 |
0.25 |
0.3 |
0.35 |
Yk |
-4.0240 |
-3.9500 |
-3.8610 |
-3.7555 |
Блок
схема:

Код
программы и её вывод:

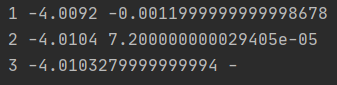
Вывод: Полученные выражения многочленов 1, 2 и 3-ей степени, а также их
значения в заданной точке b=0.21 совпадают до 2 знака после десятичной
точки.



