Вариант 3 / 1 Лабораторная

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра Информатики

Лабораторная работа №1

по дисциплине «Численные методы»

по теме:

«Методы решения нелинейных уравнений»

Вариант 3

Выполнил: студент группы БИН220*

*

Проверил:

Старший преподаватель

Юсков Игорь Олегович

Москва 2024

Задание

1. Выбрать индивидуальное задание по указанию преподавателя из табл. 1-1.

• нелинейное уравнение;

• методы решения нелинейного уравнения для выполнения 3-ч итераций;

2. Отделить корни заданного уравнения графическим и аналитическим методом;

3.  Провести исследование нелинейного уравнения для его решения.

• проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;

• выбрать начальное приближение;

• сформулировать условия этапа окончания утончения корня;

4. С использованием итерационной формулы 1-го заданного метода провести расчёт трёх итераций.

5. Оценить погрешность результата после 3-х итераций.

6. Для 2-го заданного метода выполнить решение уравнения с точность 10^-4, создав программу реализующую заданный метод. Произвести расчёт, результаты занести в таблицу 1-2.

7. Найти решение нелинейного уравнения на отделённом отрезке.

Индивидуальное задание

Вариант	Уравнение	1-ый метод	2-ой метод
3	ex-4e-x-1=0	Итерации	Хорд

Отделение корней

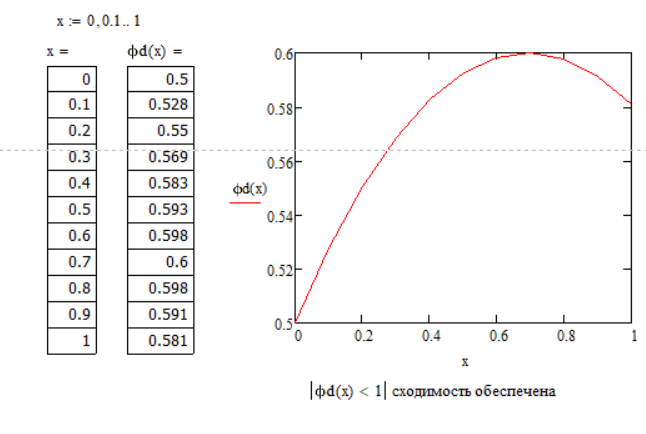
Произведем отделение корней при помощи программы Mathcad 15

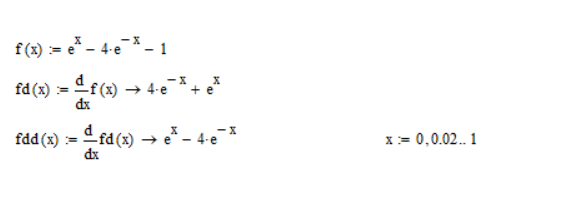
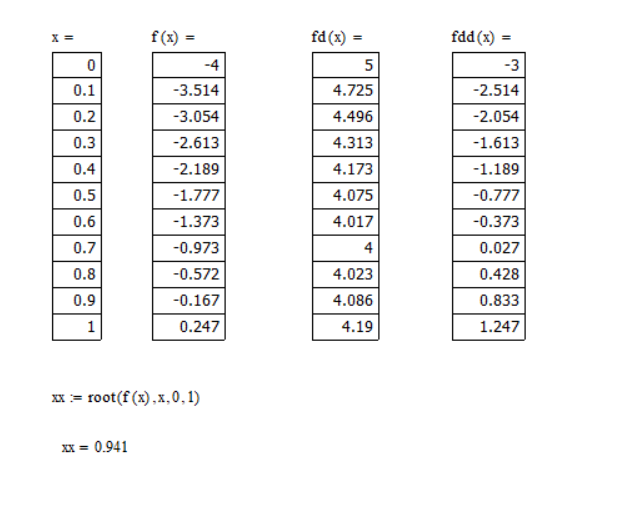
Вывод: на концах отрезка [0;1] функция имеет противоположные знаки, а 1-я производная знакопостоянна, следовательно, на этом отрезке уравнение e^x-4e^-x-1=0 имеет единственный корень.

Уточнение корней

Метод итераций

Так как привести уравнение e^x-4e^-x-1=0 к виду 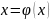напрямую нельзя, то воспользуемся формулой 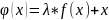, где параметр 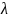определён правилом 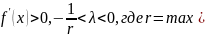. Для сходимости процесса итерации необходимо, чтобы .

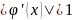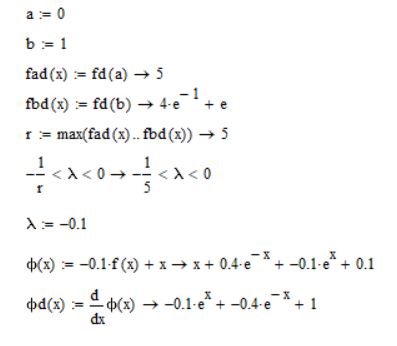
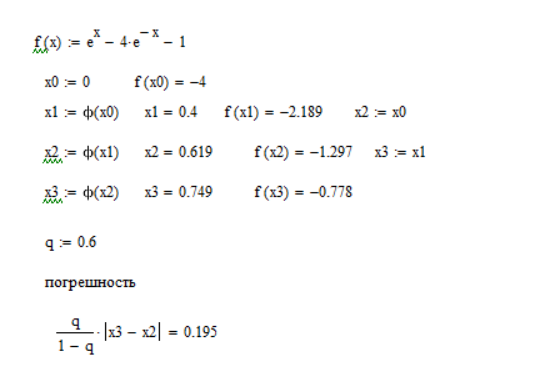
K	Xк	F(Xk)
0	0	-4
1	0.4	-2.189
2	0.619	-1.297
3	0.749	-0.778

Погрешность равна 0.195

Метод Хорд

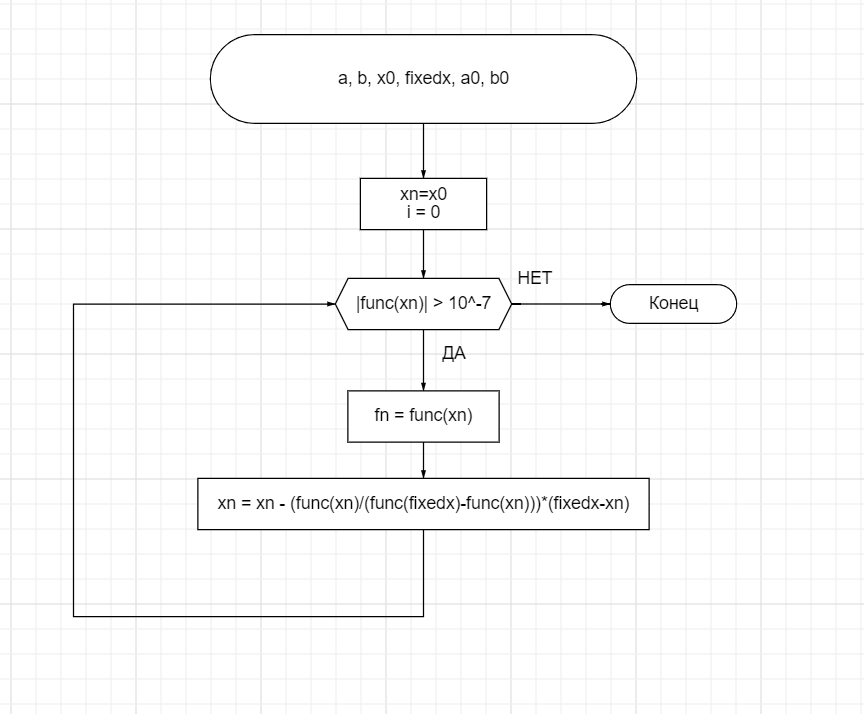
Проверка выполнения условий сходимости. Для сходимости метода необходимо знакопостоянство f(x) на отрезке [a;b].Выбор начального приближения. Вид рекуррентной формулы зависит оттого, какая из точек a или b является неподвижной. Неподвижен тот конецотрезка [a;b], для которого знак функции f(x)совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х0.Рекуррентная формула метода хорд в [1]:

f(x) − f(xn) Выше было показано, что для функции e^x-4e^-x-1=0 на отрезке[0,7;1] неподвижной точкой является точка x=b=1, так как

f(x) f 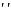(1)>0. Таким образом, полагая x0=a=0.7, получим сходящуюся последовательность приближений к корню. В рассматриваемой задаче

рекуррентная формула принимает следующий вид: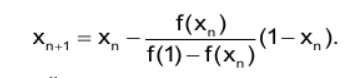

2. Расчет итераций и погрешности

Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:

N	Xn	F(Xn)
0	0.9392880936456048	-1
1	0.9406034092882514	-0.005464499380093413
2	0.9406135629938795	-4.219094105462062e-05
3	0.9406136414955502	-3.261926095898815e-07

Погрешность 2.1895708357282798e-7

Решение нелинейного уравнения: 0,941

Вывод: при помощи численных методов итераций и метода хорд был найден корень уравнение, приближение и погрешность.