МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра Информатики

Лабораторная работа №6

по дисциплине «Численные методы»

по теме:

«Одномерная оптимизация»

Вариант 17

Выполнил: студент группы БИН220*

*

Проверил:

Старший преподаватель

Юсков Игорь Олегович

Москва 2024

Задание

1. Выбрать индивидуальное задание по номеру варианта из табл. 1.6-1 для решения задачи одномерной оптимизации:

1. функцию f(x),минимум которой необходимо найти;

2. метод золотое сечение – четные номера п.3, нечетные –п.4

3. метод дихотомии - четные номера п.4, нечетные –п.3

2. Провести исследование индивидуального варианта задания:

1. построить график функции ;

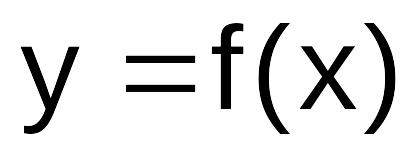2. выбрать начальный отрезок неопределенности (отрезок, содержащий точку минимума);

3. проверить выполнение аналитического условия унимодальности функции на выбранном отрезке.

3. Провести «ручной расчет» трех итераций и определить длину отрезка, содержащего точку минимума, после трех итераций.

4. Составить схему алгоритма, написать программу решения задачи оптимизации

указанным в задании методом для «расчета на ПК» и провести контрольное тестирование программы, воспользовавшись исходными данными и результатами рассмотренного примера.

5. Решить задачу оптимизации с точностью E = 10^-4с помощь написанной программы («расчета на ПК»).

6. Вычислить число итераций, необходимых, чтобы локализовать точку минимума с

точностью E1 = 10^-4, расчет сравнить с результатом, полученным на ПК.

Индивидуальный вариант:

Таблица 1

№ вар.	f(x)
17

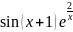
Выполнение задания

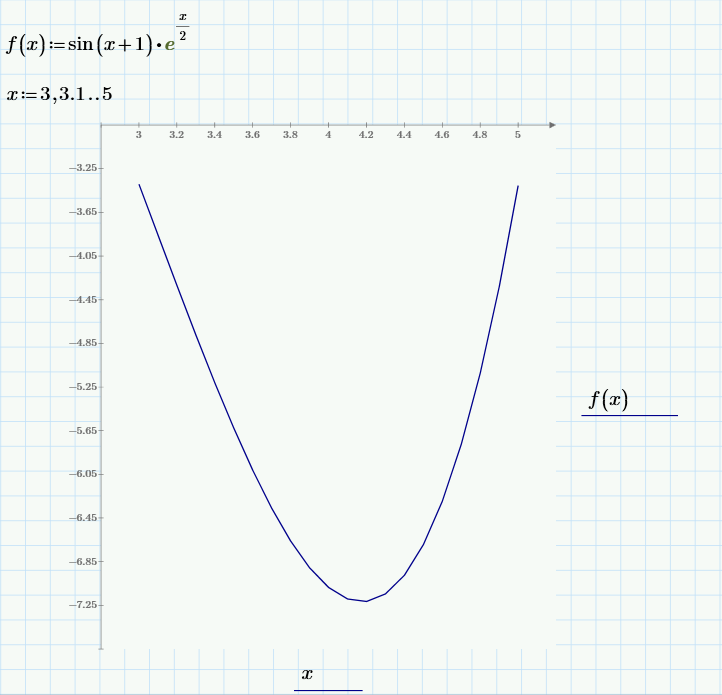
Рис.1 – График функции f(x)

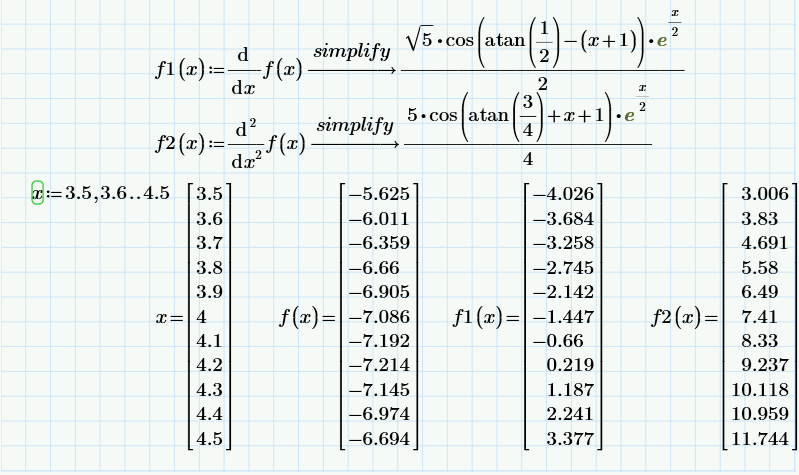
Рис.2 – Значения функции f(x) на промежутке [1;2]

На отрезке [3.5;4.5] функция f(x) дважды дифференцируема и f2(x) = fˈˈ(х*)>0 в любой точке этого отрезка, следовательно, функция f(x) унимодальная на этом отрезке.

Ручной расчёт методом дихотомии

Значение параметра метода дихотомии для ручного просчета равен d= =0.01

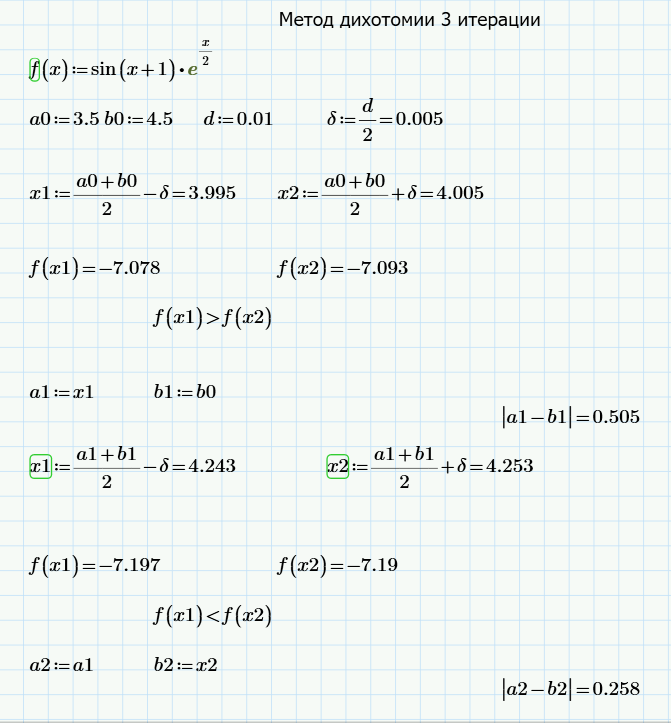
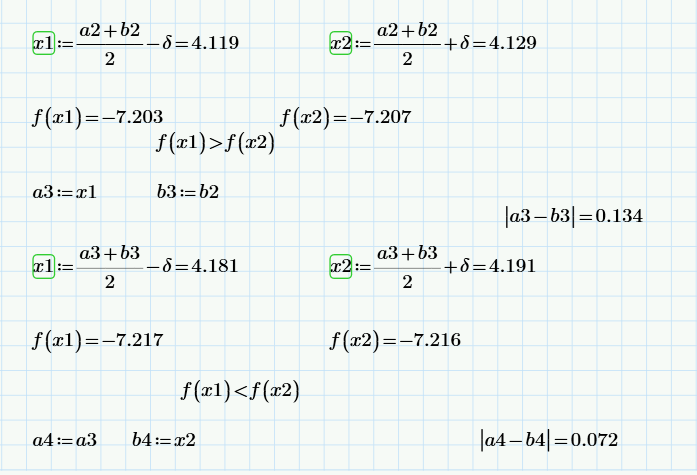
Рис.3 – расчёт 3 итераций в Mathcad

Занесём результаты расчёта в таблицу 2.

Таблица 2

N	a	b	X1	X2	F(X1)	F(X2)
1	3.5	4.5	3.995	4.005	-7.078	-7.093	0.505
2	3.995	4.5	4.243	4.253	-7.197	-7.19	0.258
3	3.995	4.253	4.119	4.129	-7.203	-7.207	0.134
4	4.119	4.191	4.181	4.191	-7.217	-7.216	0.072

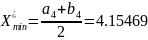, f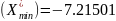

Для метода дихотомии длина отрезка неопределенности, содержащего точку минимума, после трёх итераций равна:

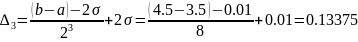
Расчёт на ПК методом золотого сечения

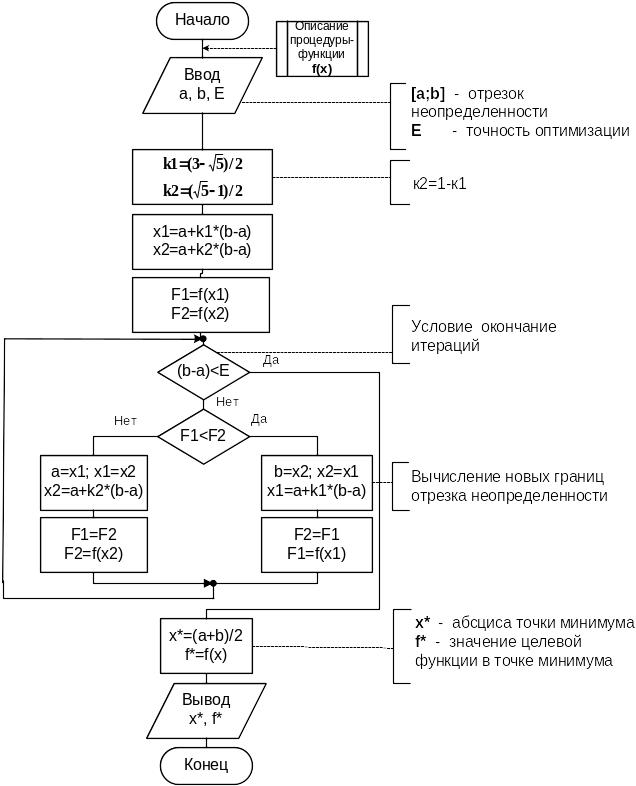
Рис. 4 – блок-схема алгоритма.

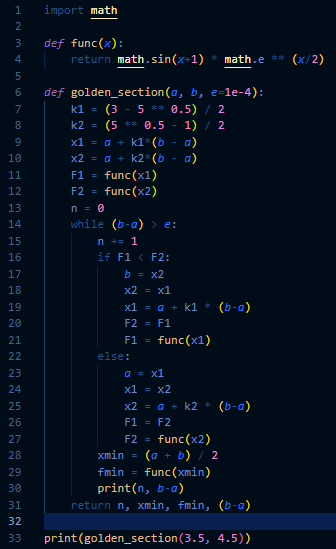
Рис.5 – код программы

Рис.6 – вывод программы

Число итераций, необходимых для локализации точки минимума:

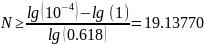
В программе при N=19 длина конечного отрезка равна 0.000106. Точность достигнута при N=20.