МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра Информатики

Лабораторная работа №5

по дисциплине «Численные методы»

по теме:

«Методы решения дифференциального уравнения»

Вариант 17

Выполнил: студент группы БИН220*

*

Проверил:

Старший преподаватель

Юсков Игорь Олегович

Москва 2024

Задание

1. Выбрать индивидуальное задание в табл. 4-1 для решения обыкновенных дифференциальных уравнений:

• дифференциальное уравнение ;

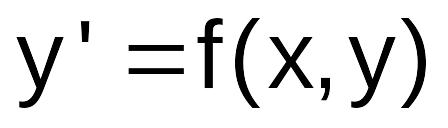• интервал [a;b] , где ищется решение дифференциального уравнения;

• начальные условия x₀, y₀;

• шаг интегрирования h_0.

2. Найти аналитическое решение 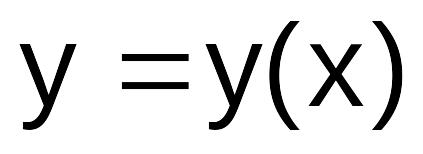заданного дифференциального уравнения, полагая его точным.

3. Вычислить значения полученного решения 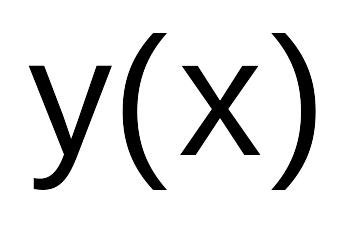на отрезке [a;b] с шагом h₀.

4. Найти численное решение дифференциального уравнения методом Эйлера - в точках отрезка [a;b] с шагом h₀ с помощью «ручного счета».

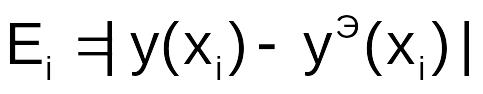5. Вычислить значения погрешностей для , , .

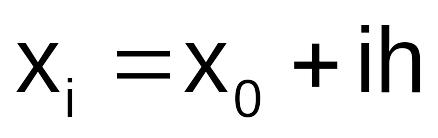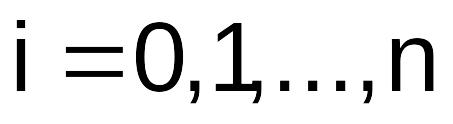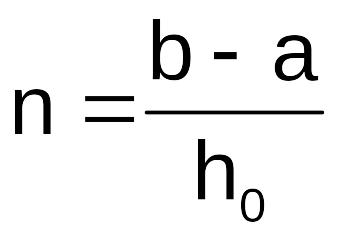6. Написать и выполнить программу, реализующую программу решения дифференциального уравнения методом Рунге-Кутта 4-го порядка yрк(х) в точках отрезка [a;b] с шагом h0, обеспечив с использованием метода автоматического выбора шага, точность 10^-4.

7. В ычислить значения погрешностей .

для x_i = x₀ + ih, i=0,1,…,n

8. Найти решение дифференциального уравнения y^s(x)

9. Графически проиллюстрировать решения .

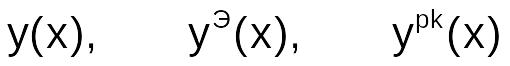Индивидуальное задание:

Таблица 1

№ вар	Уравнение	x0	y0	h0	a	b
17	y' = y2/(ex+4x)	0	-1	0.4	0	1.2

Аналитическое решение

Дифференциальное уравнение:

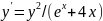
Интервал: [0; 1.2]

Начальные условия:

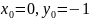
Шаг интегрирования:

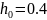
Решение ОДУ аналитическим методом:

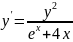
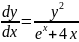
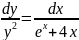
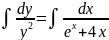
Общее решение дифференциального уравнения:

y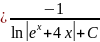

Из начальных условий , найдём константу С:

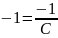
Частное решение дифференциального уравнения:

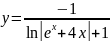
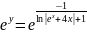
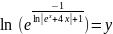
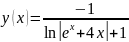
Значения точного решения ОДУ:

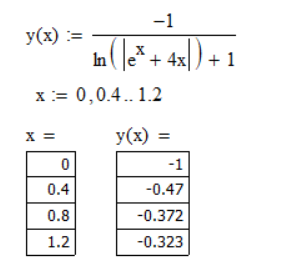
Рис. 1

Решение методом Эйлера(методом Рунге-Кутты 1-го порядка)

Рис. 2

Вычислим значения погрешностей

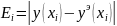для

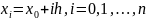
n=(b-a)/h=3

Таблица 2

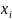
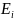
0	0
0.4	0.013
0.8	0.182
1.2	0.208

Схема алгоритма решения ОДУ с автоматическим выбором шага, обеспечивающего заданную точность

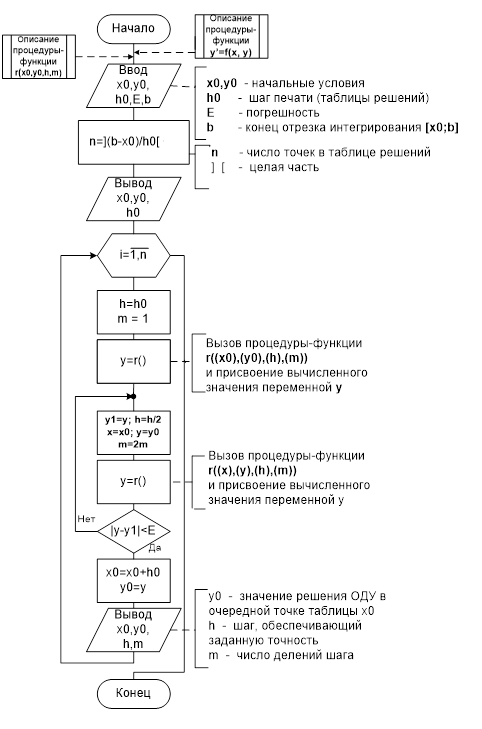
Рис.3

Программа решения ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага (Python)

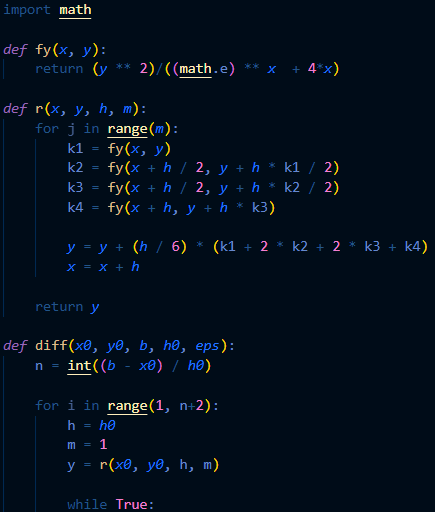
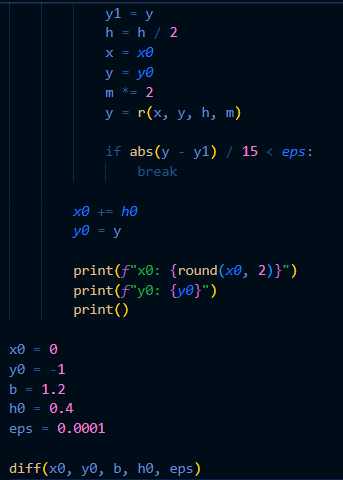
Рис.4 – код программы

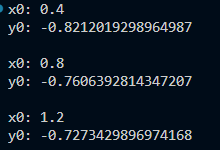
Рис.5 – Вывод программы

Таблица 3

0	-1
0.4	-0.8212019298964987
0.8	-0.7606392814347207
1.2	-0.7273429896974168

Значения погрешностей

Вычислим значения погрешностей ,

Таблица 4

0	0
0.4	0.2212
0.8	0.2072
1.2	0.1965

Все решения, полученные выше, сведем в таблицу результатов

Таблица 5

0	-1	-1	0	-1	0
0.4	-0.47	-0.6	0.013	-0.8212	0.2212
0.8	-0.372	-0.5534	0.182	-0.7606	0.2072
1.2	-0.323	-0.5308	0.208	-0.7273	0.1965

где

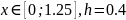
- аналитическое решение ОДУ,

- решение ОДУ, полученное методом Эйлера, ,

- решение ОДУ методом Рунге-Кутты 4-го порядка, .

Графическая иллюстрация решений , ,

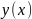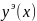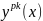
Рис.5 – графики функций