Вариант 17 / 1 / 1 Лабораторная Т

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ И МАССОВЫХ КОММУНИКАЦИЙ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра Информатики

Лабораторная работа №1

по дисциплине «Численные методы»

по теме:

«Методы решения нелинейных уравнений»

Вариант 17

Выполнил: студент группы БИН220*

*

Проверил:

Старший преподаватель

Юсков Игорь Олегович

Москва 2024

Задание

1. Выбрать индивидуальное задание по указанию преподавателя из табл. 1-1.

• нелинейное уравнение;

• методы решения нелинейного уравнения для выполнения 3-ч итераций;

2. Отделить корни заданного уравнения графическим и аналитическим методом;

3.  Провести исследование нелинейного уравнения для его решения.

• проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;

• выбрать начальное приближение;

• сформулировать условия этапа окончания утончения корня;

4. С использованием итерационной формулы 1-го заданного метода провести расчёт трёх итераций.

5. Оценить погрешность результата после 3-х итераций.

6. Для 2-го заданного метода выполнить решение уравнения с точность 10^-4, создав программу реализующую заданный метод. Произвести расчёт, результаты занести в таблицу 1-2.

7. Найти решение нелинейного уравнения на отделённом отрезке.

Индивидуальное задание

Таблица 1

Вариант	Уравнение	1-ый метод	2-ой метод
17	ex-e-x-2=0	Итерации	Половинного деления

Отделение корней

Произведем отделение корней при помощи программы Mathcad 15

Рис.1 – расчёт в Mathcad

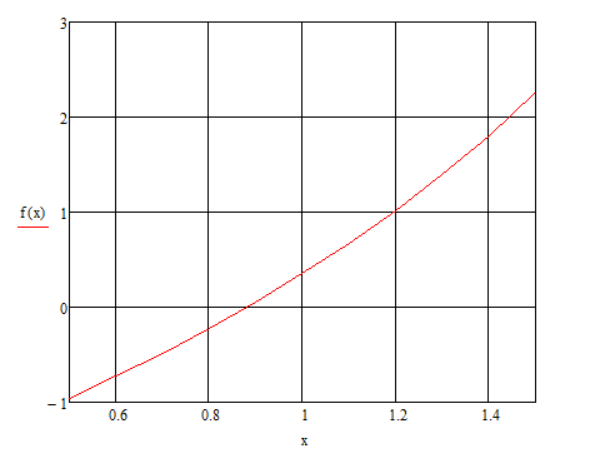
Рис.2 – график функции f(x)

Вывод: на концах отрезка [0.5;1.5] функция имеет противоположные знаки, а 1-я производная знакопостоянна, следовательно, на этом отрезке уравнение e^x-e^-x-2=0 имеет единственный корень.

Уточнение корней

Метод итераций

Так как привести уравнение e^x-e^-x-2=0 к виду 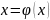напрямую нельзя, то воспользуемся формулой , где параметр определён правилом . Для сходимости процесса итерации необходимо, чтобы .

Рис. 3 – расчёт

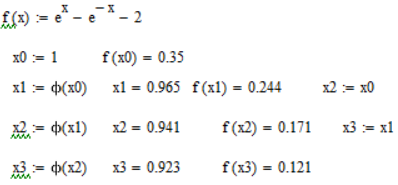
Рис.4

Таблица 2

K	Xк	F(Xk)
0	1	0.35
1	0.965	0.244
2	0.941	0.171
3	0.923	0.121

Рис.5 – расчёт погрешности

Метод Половинного деления

Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [0.5;1.5] функция f(x) = e^x-e^-x-2 меняет знак и монотонна f’(x) > 0, то условие сходимости выполняется. Начальным приближением является середина отрезка [0.5;1.5]: .

.

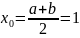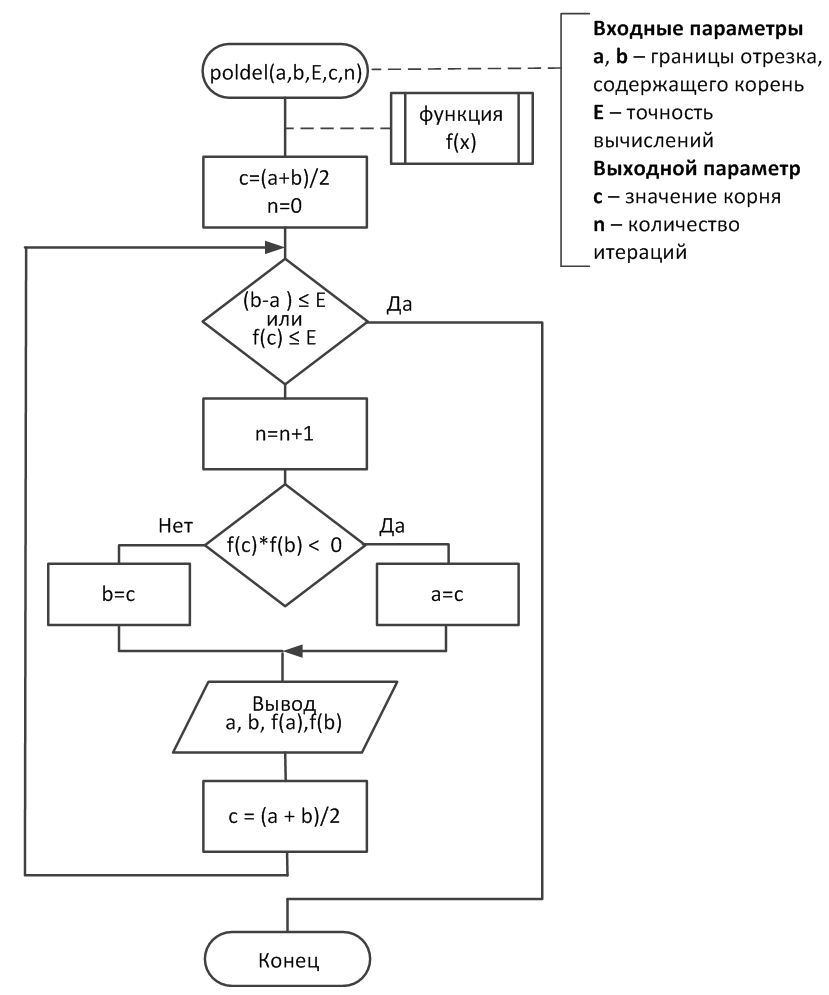
Рис.6 – блок-схема программы

Рис.7 – код программы

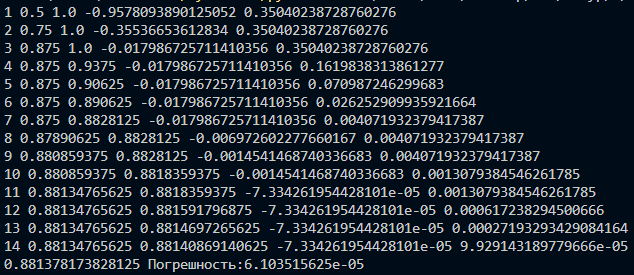
Рис.8 – вывод программы

Рис.8 – решение нелинейного уравнения

Решение нелинейного уравнения: 0,881

Вывод: при помощи численных методов половинного деления и метода итераций был найден корень уравнение, приближение и погрешность.