Семестр7 / Надійність та діагностика електрообладнання / Матеріали / Бабкін Г.В. -Надійність і діагностика електрообладнання

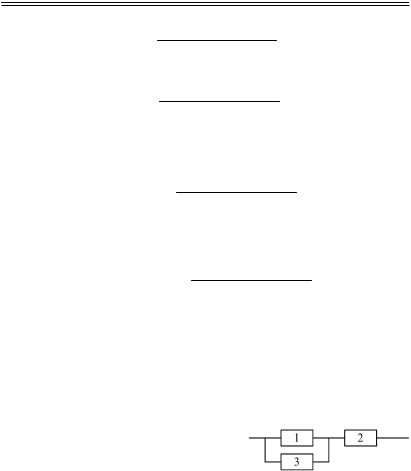
Надійність та діагностика електрообладнання

2

P1 2 2 2 2 ,

2 2

P2 2 2 2 2 .

Коефіцієнтготовностісистеми управліннядорівнює

2

Kг P0 2 2 2 2 .

Коефіцієнтпростою

2 2 2 Kп P1 P2 2 2 2 2 .

Підставляючи числовізначення,отримуємо:

Kп 10 2,

Kг 1 Kп 0,99.

Відомо також, що інтенсивність відмов блока 2 дуже

мала в порівнянні з інтенсивностями відмов і блоків 1

і3 (тобто ) іпристрій експлуатується в умовахобмеженого відновлення. Потрібно визначити коефіцієнти

91

Г.В. БАБКІН

готовності Kг і простою Kп. Інтенсивність відмов і відновлення пристрою рівнівідповідно і , причому .

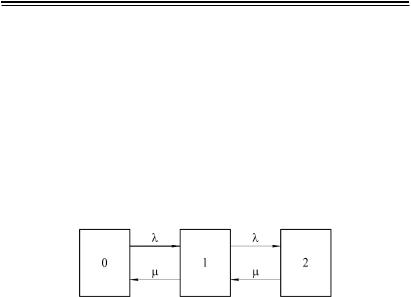
Розв’язання. Якщо припустити, що наявність у системі блока2непогіршуєїїнадійності,томожнавиділити наступні три стани, в яких може перебувати пристрій:

0 – блоки 1 і3 справніісистема керування працездатна; 1 – один з блоків (1 або 3) пошкоджений іремонтується,

асистема, якіраніше, зберігаєпрацездатність; 2–обидваблоки(1і3), аотже, ісистемав ціломунепра-

цездатна.

Схема перерахованих станів наведена на рис. 9.9.

Рис. 9.9

Позначимо ймовірності зазначених станів у певний момент часу t відповідно P0(t), P1(t) та P2(t).

Очевидно, що

Ясно, що Kг= P0+P1, оскільки перехід системи зістану0 встан 1(0 1)невідображаєтьсянаїїпрацездатності,аKп=P2

або Kп = 1+Kг, тому що P0+P1+P2 = 1.

Запишемо рівняння, що відповідають схемі станів пристрою. Відповідно до (9.5) ірис. 9.9,

P0 t P0 t P1 t ;

P1 t P0 t P1 t P2 t ;

P2 t P1 t P2 t .

92

Надійність та діагностика електрообладнання

Доповнивши систему рівнянь нормувальною умовою (9.7), при t маємо

P0 P1 0;

P0 P1 P2 0;

P1 P2 0;

P0 P1 P2 1.

Спільнерозв’язання1-го, 2-го і4-горівнянь системи дає наступнийрезультат:

2

P0 1 1,

P1 1 1,

1

P2 1 1,

де .

Оскільки за умовами задачі, то, підставивши це значення в формули ймовірностей станів системи,

отримаємо P0=P1=P2 = 0,3333, тому Kг = P0+P1=0,6666, Kп = P2=1–Kг = 0,3333.

Задача 9.4. Перетворювач складається з робочого блока іблокав ненавантаженомурезерві. Розподілчасів між відмовами і відновлення показові з параметрами 1/год та 1/год. Потрібно знайти значення коефіцієнтів простоюівскільки разівзменшуєтьсявеличинакоефіцієнтапростоюперетворювачапризастосуваннінеобмеженого відновлення в порівнянніз обмеженим.

93

Г.В. БАБКІН

Розв’язання. Для визначення значень коефіцієнтів простою длявипадків обмеженого інеобмеженого відновлення скористаємося відповідно виразами (9.8) і(9.9). Число можливихстанів дорівнює трьом.

Дляобмеженого відновлення

Для даноїзадачісправедливеспіввідношення , іотриманівиразиможуть бутиз достатньоюдляпрактикиточністю визначенінаближено:

2

Kп.о. 2 ,

2

Kп.н. 2 2 .

Такимчином,призастосуваннінеобмеженоговідновлення впорівняннізобмеженимвеличинакоефіцієнтапростоюзменшиласявдварази. Значенняцихкоефіцієнтів дорівнюють:

Kп.о. 10 4,

Kп.н. 0,5 10 4.

94

Надійність та діагностика електрообладнання

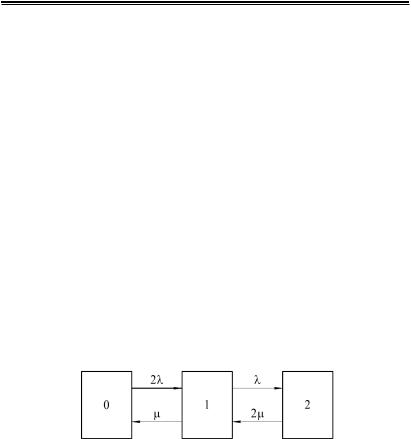
Задача9.5.Перетворювачелектропривода,щоскладається з робочого блока іблока в навантаженомурезерві, розрахований на безперервну цілодобовуроботу. Через три години післявключенняцей пристрій можеотримати командуна перебудовурежимуроботи.Інтенсивністьвідмовівідновленнякожногоблокарівні 1/год, 1/год. Єдвічерговіремонтнібригади. Визначити ймовірність застати перетворювач у непрацездатному стані через три години після включення(значенняфункціїпростою)ізначеннякоефіцієнта простою.

Розв’язання. Перетворювач електропривода в будь-який момент часуможе знаходитисяв одномуз наступнихстанів:

0 – обидва блоки працездатні;

1– один блок непрацездатний;

2– обидва блоки непрацездатні.

При знаходженні в станах 0 і 1 пристрій працездатний, устані2–пристрій непрацездатний. Схема станів пристрою з відповідними інтенсивностями переходів представлена на рис. 9.10.

Рис. 9.10

Системадиференціальнихрівнянь,складеназацієюсхемою, має вигляд

P0 t 2 P0 t P1 t ;

P1 t 2 P0 t P1 t 2 P2 t ;

P2 t P1 t 2 P2 t .

95

Г.В. БАБКІН

Длявизначенняфункціїпростоюрозв’яжемоцюсистему при початкових умовах P0(0)=1 та P1(0)=P2(0)=0. Переходячи до зображень,отримуємо системуалгебраїчнихрівнянь:

s 2 P0 s P1 s 1;

2 P0 s s P1 s 2 P2 s 0;

P1 s s 2 P2 s 0.

Для отримання величин Pi(s) використовуємо правило Крамера:

Pi s i ,

де – визначник, елементами якого є коефіцієнти при P0(s),

P1(s) та P2(s);

i –визначник, який утворюєтьсяз шляхом заміни i-го стовпцякоефіцієнтами правоїчастини системи.

Вданомувипадкупотрібно визначити функціюпростою, рівнуP2(t). Для цього запишемо визначники і 2:

Отже,

2 2

P2 s s s2 3 s 4 2 2 2 2 .

96

Надійність та діагностика електрообладнання

Знайдемо коріньрівняння

s2 3 s 2 2 0.

97

Г.В. БАБКІН

Оскільки

Підставляючи числовізначення, отримуємо

Kп 3 2 10 4,

Kп 1,5 10 3.

Задача 9.6. Система керування приводом складається з робочого блока іблока в ненавантаженомурезерві. Інтенсивність відмов і відновлення кожного блока дорівнюють

1/год, 1/год.

При одночасній несправностіобох блоків система керування непрацездатна. Визначити середній час безвідмовної роботи системи mt.

Розв’язання. Система керування приводом у будь-який момент часуможе знаходитисяв одномуз наступнихстанів:

0 – обидва блоки працездатні;

1– один блок непрацездатний;

2– обидва блоки непрацездатні.

Схема станів системи представлена на рис. 9.11.

98

Надійність та діагностика електрообладнання

Рис. 9.11

Для визначення mt спочатку необхідно визначити ймовірність безперервної безвідмовної роботи протягом часу t. Система диференціальних рівнянь, отримана за схемою станів, маєтакий вигляд:

P0 t P0 t P1 t ;

P1 t P0 t P1 t ;

P2 t P1 t .

Початковіумови

P0 0 1, P1 0 P2 0 0.

За допомогою перетворення Лапласа отримуємо системуалгебраїчнихрівняньщодо зображень:

s P0 s P1 s 1;

P0 s s P1 s 0;

P1 s s P2 s 0.

Шляхом розв’язання цієїсистеми або підстановкою, або за правилом Крамера отримаємо

2

P2 s s s s1 s s2 .

99

Г.В. БАБКІН

Розкладаючи P2(s) на елементарні дроби і роблячи зворотне перетворення Лапласа, визначаємо ймовірність P2(t) попадання за час (0, t) устан 2:

Отже, ймовірність безперервноїбезвідмовноїроботиобчислювального пристрою за час (0, t) дорівнює

Задача9.7. Перетворювачприводаміститьробочий блок іблокунавантаженомурезерві.Інтенсивністьвідмовівідновлення кожного блока рівні відповідно і . Час супроводу в середньомустановить величину tc. При одночасній непрацездатностіобохблоківвідбуваєтьсявідмоваперетворювача. При переході на резервний блок відмова перетворювача не відбувається.

Потрібно визначитиймовірністьбезперервноїбезвідмовної роботи протягом часу (0, tc), або, інакше кажучи, ймовірність непотрапляннявстан2нацьомуінтерваліісередній час безвідмовноїроботи перетворювача mt.

100