Семестр6 / ТАК / Курсова робота / 3361__Лр

Лабораторні роботи. Синтез САК

Тема: Синтез систем автоматичного керування методом прямих ЛАЧХ

Основні теоретичні відомості

Відповідно до класифікації САР можна поділити на три типи систем: стабілізуючі, програмні та слідкуючі. З них у даний час у різних галузях транспорту і виробництва все більше застосування знаходять слідкуючі системи, різноманітні як за призначенням, так і за будовою. Незважаючи на те, що ці системи перебувають у різних експлуатаційних умовах і до них ставляться різні тактико-технічні вимоги, які повинні певним чином ураховуватися при проектуванні кожної з них, методи їхнього синтезу залишаються в основному загальними. Загальність методів синтезу пояснюється загальністю структури та принципів побудови. Характерна риса структурних схем слідкуючих систем полягає в тому, що вони містять ряд паралельних ланцюгів зворотних зв'язків, які охоплюють ту саму послідовність ланок. Для синтезу таких систем часто використовують метод зворотних логарифмічних частотних характеристик (ЗЛЧХ).

Поряд з методом реалізації зворотної бажаної ЛАЧХ одним з найпоширеніших частотних методів синтезу коригувальних пристроїв є метод прямих логарифмічних частотних характеристик. Він проводиться в такий спосіб:

• будується бажана логарифмічна амплітудна частотна характеристика, виходячи з необхідної точності системи та необхідної якості перехідного процесу;

• ця характеристика порівнюється з нескоригованою системою;

• визначається передавальна функція коригувального пристрою так, щоб при його включенні в систему, була б отримана бажана форма логарифмічної амплітудної характеристики.;

• потім будується фазова частотна характеристика і оцінюється величина отриманого при цьому запасу стійкості системи та інших якісних показників.

Завдання

Варіант №1

Передаточна функція системи в розімкнутому стані:

, синтезувати послідовний коректувальний пристрій, щоб у замкнутому стані ця система виконувала наступні показники якості: , .

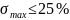1. Побудова ЛАЧХ незмінної частини системи

Побудуємо ЛАЧХ незмінної частини системи:

За допомогою передаточної функції незмінної частини системи ( ) побудуємо ЛАЧХ незмінної частини системи, для цього знайдемо коефіцієнт підсилення та спряжуючі частоти:

,

Так як ми нумеруємо спряжуючі частоти за порядком зростання, враховуючи значення частот, знайдених далі за розрахунками, пронумеруємо спряжуючі частоти як та відповідно:

,

,

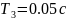Знаючи коефіцієнт підсилення: та спряжуючі частоти: та , побудуємо, у програмі КОМПАС-3D, графік ЛАЧХ незмінної частини системи (рис. 1):

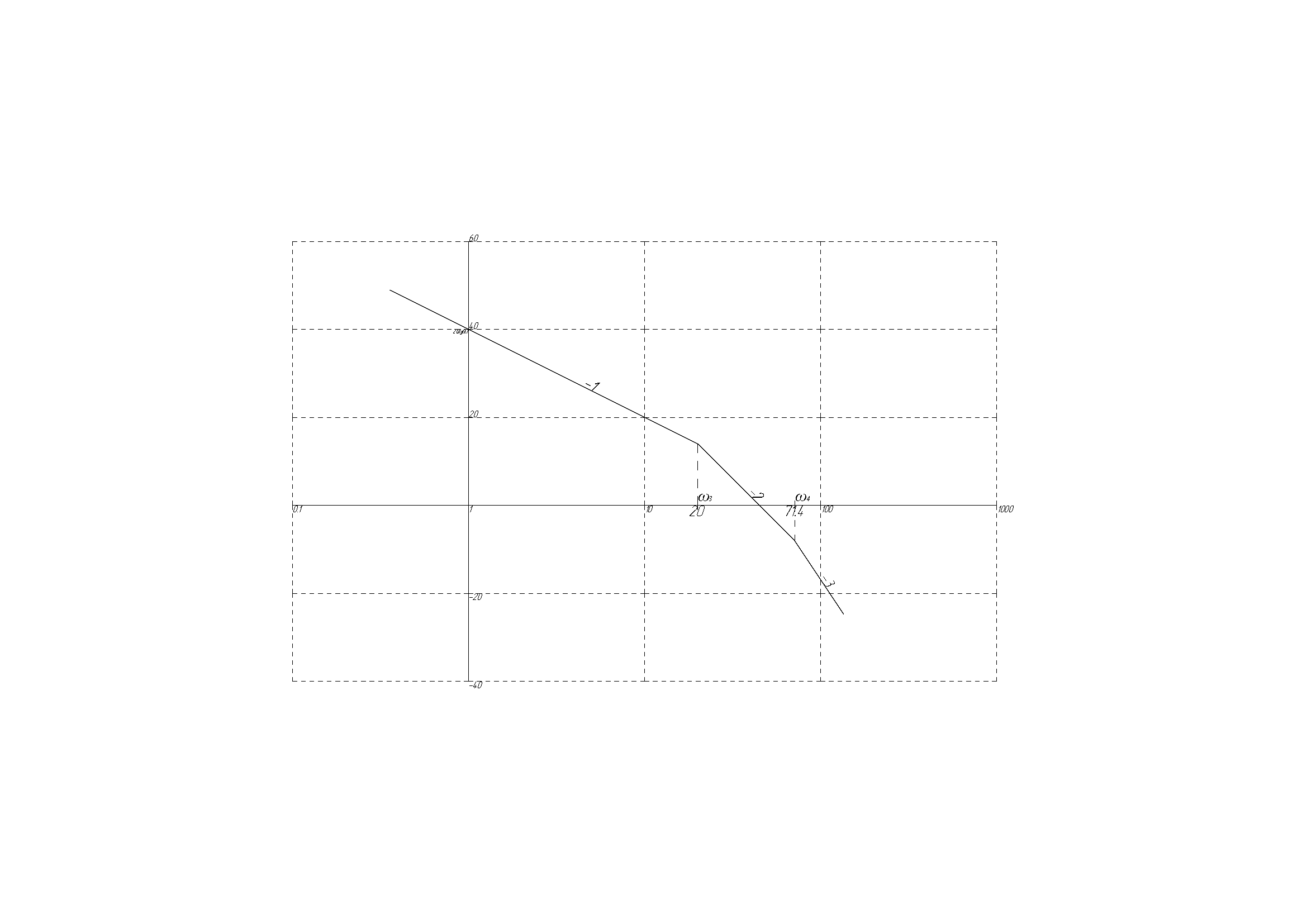
Рисунок 1 – ЛАЧХ незмінної частини системи

2. Побудова ЛАЧХ бажаної частини системи

Розглянемо формування бажаної ЛАЧХ, виходячи із заданих вимог до системи за точністю і якістю перехідного процесу. Вважаємо заданими значення показників якості перехідного процесу:

σ_max  максимальне перерегулювання;

t_p  максимальний час регулювання.

Побудову середньочастотної асимптоти бажаної ЛАЧХ починають із вибору частоти зрізу ω_зр. Для цього використовується номограма на рис. 1.4 [1, с. 18], розроблена В.В. Солодовніковим. Вона визначає залежність перерегулювання σ_max і часу регулювання t_p від максимуму Р_max дійсної частотної характеристики замкненої системи, причому час регулювання t_p дано у вигляді функції частоти зрізу ω_зр.

Номограма використовується в такий спосіб. За заданим значенням перерегулювання σ_max визначають значення P_max. Потім по Р_max визначають співвідношення між t_p і ω_зр.

Середньочастотна асимптота бажаної ЛАЧХ проводиться через точку ω_зр із нахилом –20 дБ/дек. При більшому нахилі важко забезпечити необхідний запас стійкості та припустиме перерегулювання.

Для зазначеного вибору за раніше знайденим значенням P_max за допомогою кривих, показаних на рис. 1.5 [1, с. 19], визначають надлишок фази γ та граничні значення L_м логарифмічних амплітуд.

Для побудови сполучаючої асимптоти, спочатку потрібно провести пряму з ординатою L_м. Потім нанести сполучаючу асимптоту. Якщо нахил низькочастотної асимптоти –20 дБ/дек, то нахил сполучаючої асимптоти вибирається рівним –40 або –60 дБ/дек.

Починати спрягаючу асимптоту можна із точки середньочастотної асимптоти з ординатою L_м.

Рішення:

Побудуємо ЛАЧХ бажаної частини системи:

Для цього, за допомогою максимального перерегулювання ( ), використовуючи першу номограму, на рис. 1.4 [1, с. 18], знаходимо значення: , та час регулювання: , звідси знаходимо частоту зрізу, знаючи час регулювання ( ):

Далі, за допомогою другої номограми на рис. 1.5 [1, с. 19] знайдемо граничні значення: , та надлишок фази: .

Знаючи частоту зрізу: та граничні значення: , побудуємо графік ЛАЧХ бажаної частини системи (рис. 2):

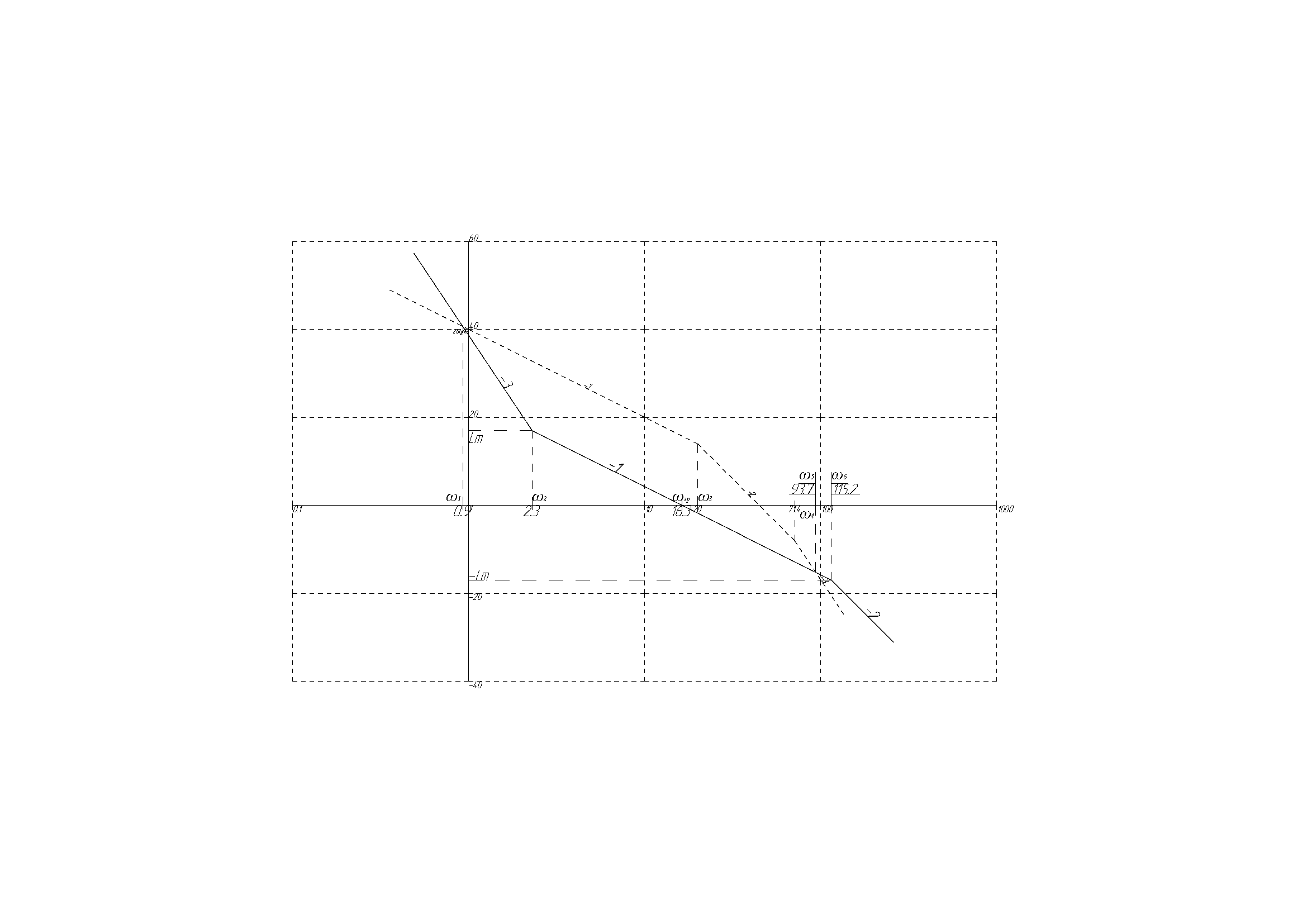
Рисунок 2 – ЛАЧХ бажаної частини системи

Побудувавши ЛАЧХ бажаної частини системи, ми можемо знайти частоти цього графіка:

, , , ,

, .

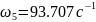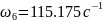Та розрахувати постійні часу:

, , , , ,

.

Таким чином, ми можемо побудувати передаточну функцію бажаної частини системи:

Змоделюємо передачу функцію бажаної частини системи в Matlab (рис. 3):

Рисунок 3 – Схема бажаної системи в Matlab

Далі побудуємо перехідну характеристику (рис. 4), ЛАЧХ та ЛФЧХ (рис. 5) бажаної частини системи, для того щоб знайти: значення перерегулювання, час регулювання, запас стійкості по фазі та запас стійкості по амплітуді:

Рисунок 4 – Перехідна характеристика бажаної системи в Matlab

Маємо значення перерегулювання: , та час регулювання: , статична помилка відсутня. Показники якості вписується в потрібні межі: та .

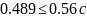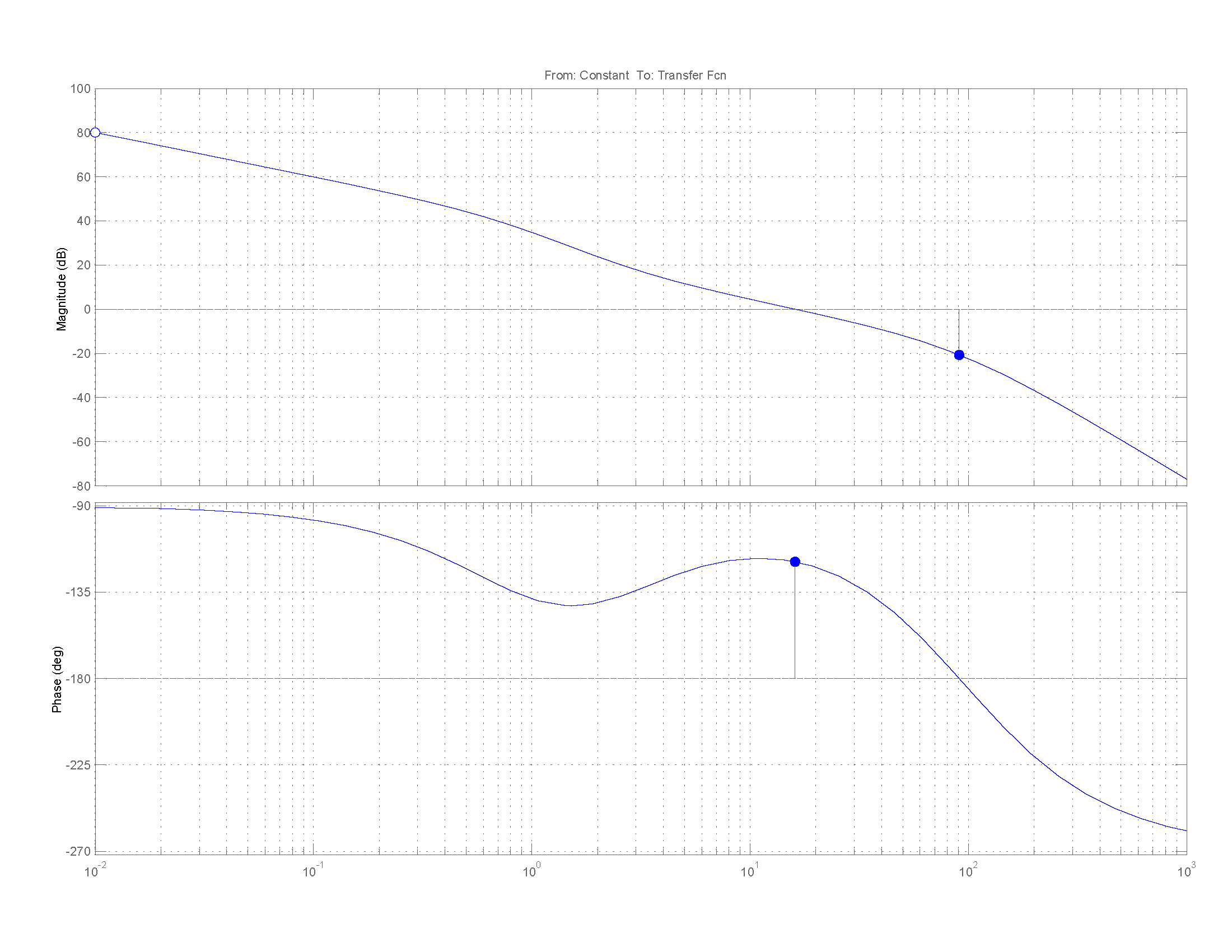
Рисунок 5 – ЛАЧХ та ЛФЧХ бажаної системи в Matlab

Маємо запас стійкості по амплітуді: , та запас стійкості по фазі: .

2. Синтез коригувальних пристроїв

При виборі типу коригуючої ланки (послідовної або паралельної) проектувальник має виважено оцінити всі недоліки та переваги того чи іншого варіанту.

Перевага послідовних коригувальних пристроїв полягає в тому, що вони часто можуть бути виконані у виді простих пасивних RC - контурів. Основним їхнім недоліком можна вважати те, що мінливість параметрів і характеристик елементів системи знижує ефективність дії послідовних коригувальних пристроїв, тому ставляться підвищені вимоги до стабільності характеристик елементів при їхньому застосуванні.

Інтегруючі (ті, що створюють відставання по фазі) RC-контури, які включаються послідовно, звичайно містять більш громіздкі конденсатори, ніж контури в колі зворотного зв'язку, а диференціюючі (ті, що створюють випередження по фазі) RC-контури дуже чутливі до перешкод.

Переваги паралельних коригувальних пристроїв полягають у наступному:

• зменшення залежності динамічних властивостей системи від змін параметрів і характеристик елементів, які входять до її складу, тому вимоги до елементів можуть бути не такими жорсткими, як при застосуванні послідовних коригувальних пристроїв;

• в елементах систем автоматичного регулювання, близьких до її виходу, розвивається значна потужність, тому живлення паралельного коригувального пристрою навіть у тому випадку, коли він споживає значну кількість енергії, не викликає ускладнень;

• системи з паралельними коригувальними пристроями, не так піддаються впливу перешкод, які часто бувають в сигналі помилки, як системи з послідовними коригувальними пристроями; це пояснюється тим, що елементи системи, які включаються перед входом коригувальних пристроїв, відіграють роль фільтру низьких частот.

Недоліком паралельних коригувальних пристроїв є те, що вони часто складаються з дорогих або громіздких елементів (наприклад, тахогенератори або стабілізуючі трансформатори). Значні труднощі іноді виникають у зв’язку з вимогою до зворотного зв'язку не навантажувати попередні каскади посилення. У випадку застосування паралельних коригувальних пристроїв звичайно необхідні високі коефіцієнти підсилення.

Щоб знайти передаточну функцію коригувального пристрою: . Для цього зводимо на один графік ЛАЧХ для бажаної частини системи: , та незмінної частини системи: .

Оскільки потрібно, щоб:

то можна записати (після підстановки ) наступне:

Звідки:

Отже, щоб знайти логарифмічну характеристику для , потрібно відняти характеристику від .

Рішення:

Визначимо ЛАЧХ коригувального пристрою (рис. 6):

Рисунок 6 – Визначення ЛАЧХ коригувального пристрою

Передаточна функція коригувальної системи :

Далі, побудуємо передаточну функцію скоригованої системи:

Змоделюємо передачу функцію скоригованої системи в Matlab (рис. 7):

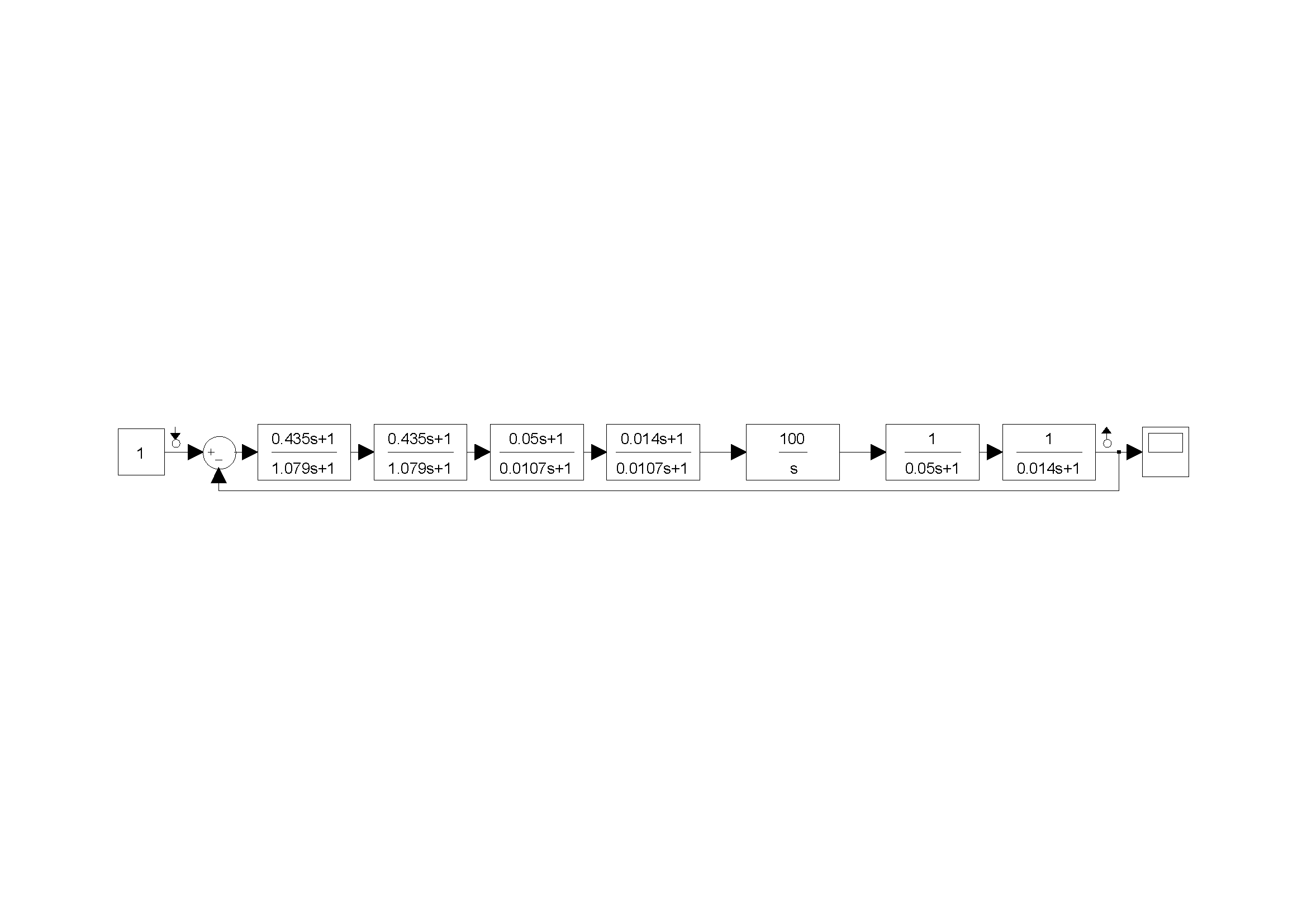
Рисунок 7 – Схема скоригованої системи в Matlab

Далі побудуємо перехідну характеристику (рис. 8), ЛАЧХ та ЛФЧХ (рис. 9) скоригованої системи, для того щоб знайти: значення перерегулювання, час регулювання, запас стійкості по фазі та запас стійкості по амплітуді:

Рисунок 8 – Перехідна характеристика скоригованої системи в Matlab

Маємо значення перерегулювання: , та час регулювання: . Результати ідентичні отриманим раніше показникам якості (рис. 4 та рис. 8).

Рисунок 9 – ЛАЧХ та ЛФЧХ скоригованої системи в Matlab

Маємо запас стійкості по амплітуді: , та запас стійкості по фазі: . Результати ідентичні отриманим раніше запасам стійкості (рис. 5 та рис. 9).

Висновок

При виконанні даних лабораторних робот я навчився синтезувати послідовний коректувальний пристрій з потрібними значеннями показників якості.

При виконанні робот, я отримав передаточну функцію скорегованої системи:

Після моделювання цієї передавальної функції в Matlab, я отримав наступні показники якості: перерегулювання: , та час регулювання: , що вписується в потрібні межі: та . Це означає, що синтез коригувального пристрою виконаний вірно.