10) Волновой характер решения. Диаграмма направленности.
Мощность и сопротивление излучения.
Понятие о волновом характере электромагнитного поля.
В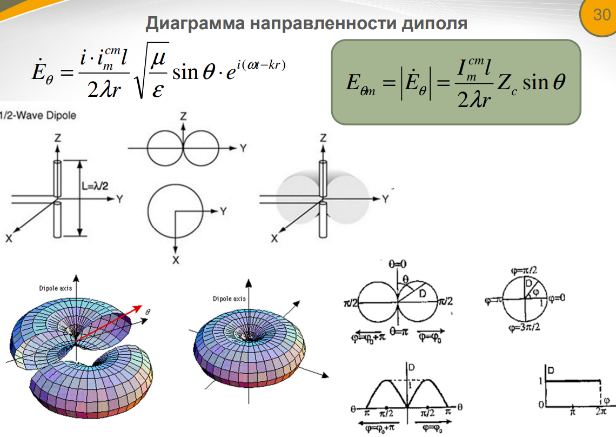
макроскопическом объеме электромагнитное
поле смещается в пространстве в виде
волн. Волновой характер смещения поля
заключается в том, что не существует
мгновенной передачи взаимодействия
поля со средой. В отличие от других
видов передачи энергии (тепла, звука)
здесь взаимодействие проявляется не
на молекулярном уровне. Изменение поля
является функцией времени и зависит
от параметров среды
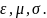Электромагнитное поле может существовать
и смещаться даже в вакууме
.
Вектор
в любой точке пространства перпендикулярен
радиусу-вектору
, а вектор
– касателен к параллелям. Излучение
электромагнитной энергии происходит
в радиальных направлениях и вектор
Пойнтинга
направлен по радиусу-вектору
:
Следовательно,
векторы
,
и
образуют правостороннюю ортогональную
тройку векторов, а поле излучения имеет
линейную поляризацию.
Важнейшей
характеристикой излучения антенн и,
соответственно, ЭЭД, является мощность
излучения
Мощность, излучаемая диполем, определяется
интегрированием вектора Пойнтинга по
поверхности
произвольной сферы в дальней зоне:
11) Понятие о локально плоской волне. Декартова система
Координат для ее описания.
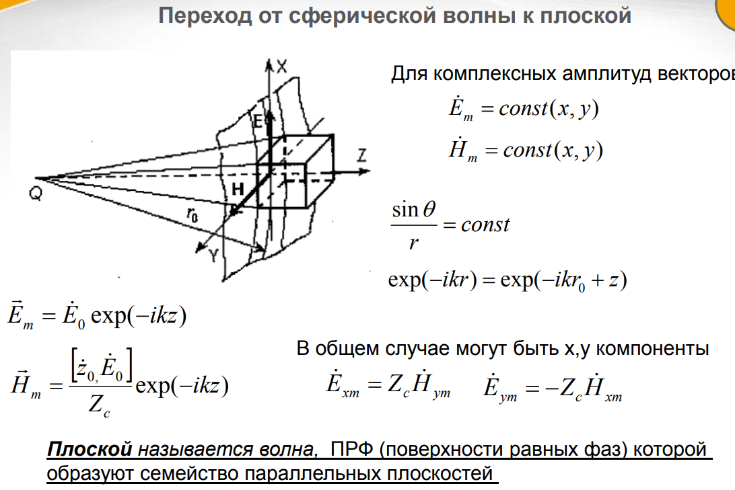
В том случае если волна распространяется в однородной среде, то ее движение в общем случае описывают волновым уравнением (дифференциальным уравнением в частных производных):
В
плоской волне во всех точках поверхности
равных фаз (ПРФ)
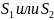векторы
имеют одни и те же значения амплитуд и
их направлений. В общем случае векторы
могут иметь по две составляющие, но в
всегда взаимно перпендикулярны и
зависят только от одной координаты z;
поэтому частные производные в декартовой
системе координат
При
распространении волны в направлении
z > 0
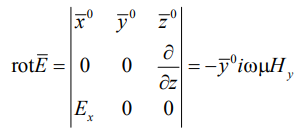
Или
Аналогично
находим:
Дифференцируя
повторно выражение (1) и подставляя в
уравнение (2), приходим к скалярному
уравнению Гельмгольца второго порядка:
Или
Уравнение является однородным, так как в плоской волне отсутствуют сторонние источники.
Р
ешив
уравнение, получим:
произвольная
комплексная амплитуда проекции вектора
падающей (бегущей) волны на ось
.
Решение
для вектора
получается из второго уравнения
Максвелла:
Комплексная амплитуда вектора напряжённости магнитного поля равна
Мгновенное
значение для гармонических векторов
определяется как
:
В
еличины
векторов E и H являются функциями времени
и пространства, что указывает на волновой
характер электромагнитного поля.
12) Понятие о локально плоской волне. Декартова система координат для ее описания. Плоская волна в среде с потерями.
И
з
11.
Волна называется плоской и однородной, если гармонические векторы поля зависят только от одной координаты, например z.
Реальные
среды всегда имеют потери и их проводимость
Среда с потерями характеризуется:
комплексным
волновым числом
или
постоянной распространения
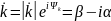
Где
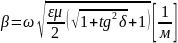
Комплексный вектор напряжённость электрического поля
13)Коэффициент затухания и распространения. Плоская волна в
реальном диэлектрике и проводнике.
Из
12.
1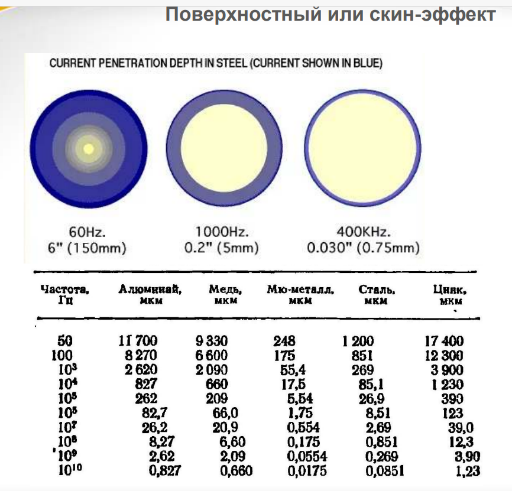
4)
Приближенное
граничное условие Леонтовича-Щукина.
Поверхностный эффект. Поляризация
плоских волн.
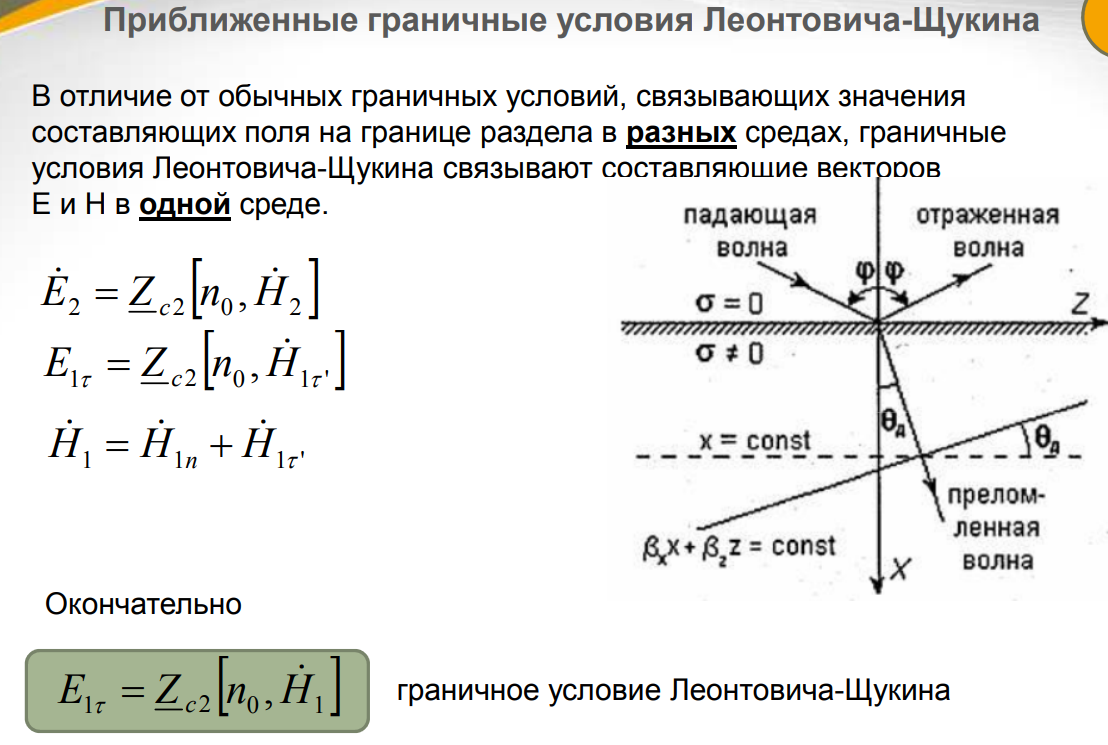
Поляризация называется линейной, если плоскость поляризации с течением времени не меняет своего положения в пространстве.
На границе двухслойной среды, например воздух – земля, линейная поляризация бывает двух видов в зависимости от ориентации вектора относительно плоскости распространения.
Поляризацию
называют горизонтальной
или нормальной,
если вектор
перпендикулярен плоскости распространения,
либо параллелен, например, поверхности
земли.
Поляризацию
называют вертикальной
или параллельной,
когда вектор
лежит в плоскости распространения. В
этом случае плоскости поляризации и
распространения совпадают.
Поляризация поля называется вращающейся, если плоскость поляризации вращается, делая один оборот за период переменного ЭМП.
П
оляризация
поля называется вращающейся,
если плоскость поляризации вращается,
делая один оборот за период переменного
ЭМП.
При этом типе поляризации векторы электрического и магнитного поля вращаются в плоскости распространения радиоволны. Вращение их происходит по синусоидальному закону с угловой скоростью вращения равной угловой частоте (т.е. вращение происходит с частотой сигнала).
Вращающаяся поляризация получается из двух когерентных (w = const) линейно поляризованных волн, имеющих ортогональные плоскости поляризации и неравные начальные фазы.
Поляризация
называется круговой, если вектор
ЭМВ в фиксированной точке пространства
вращается вокруг направления
распространения, описывая своим концом
окружность
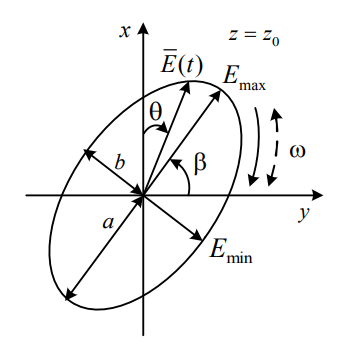Поляризация
называется эллиптической,
если вектор
ЭМВ в некоторой точке пространства
вращается вокруг направления
распространения, описывая своим концом
эллипс. При изменении координаты
распространения z вектор
описывает своим концом эллиптическую
винтовую линию, оставаясь нормальным
(для ТЕМ) к направлению распространения.
Эллиптическая поляризация получается
в результате суперпозиции двух волн
одинаковой частоты, линейно поляризованных
во взаимно перпендикулярных плоскостях