
Лаб_6 Головков И.Е. 12002108 АЭВМ
.docxБЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»
(НИУ «БелГУ»)
ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
Кафедра информационных и робототехнических систем
Отчет
по дисциплине «Архитектура ЭВМ и вычислительных систем»
специальности Информационные системы и технологии
профиль «Информационно-управляющие системы»
Лабораторная работа № 6 по теме
«Инфологические основы ЭВМ. Системы счисления. Перевод чисел»
Вариант № 5
Выполнил:
студент очной формы обучения
группы 12002108
Головков Игорь Евгеньевич
Проверила:
Доцент кафедры ПИиИТ, к-т техн. наук
Явурик Ольга Васильевна
БЕЛГОРОД 2022
Цели работы: освоить способы изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения.
Задание
Создать программу перевода чисел из одной системы счисления в другую согласно следующих вариантов:
-
5
147(10)=>(2)
11001100(2)=>(10)
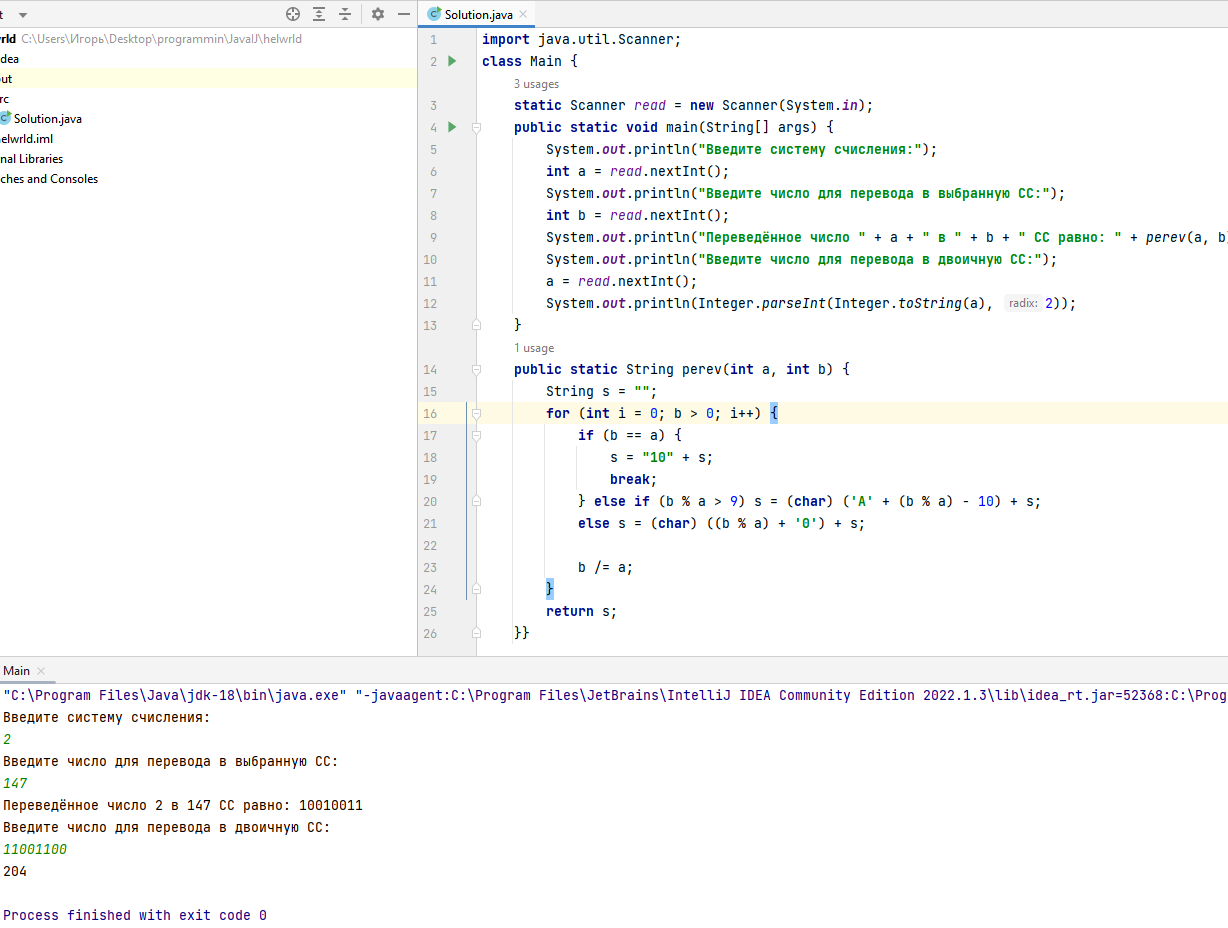
Рисунок 1 – Программа и результат её выполнения
Листинг кода программы:
import java.util.Scanner; class Main { static Scanner read = new Scanner(System.in); public static void main(String[] args) { System.out.println("Введите систему счисления:"); int a = read.nextInt(); System.out.println("Введите число для перевода в выбранную СС:"); int b = read.nextInt(); System.out.println("Переведённое число " + a + " в " + b + " СС равно: " + perev(a, b)); System.out.println("Введите число для перевода в двоичную СС:"); a = read.nextInt(); System.out.println(Integer.parseInt(Integer.toString(a), 2)); } public static String perev(int a, int b) { String s = ""; for (int i = 0; b > 0; i++) { if (b == a) { s = "10" + s; break; } else if (b % a > 9) s = (char) ('A' + (b % a) - 10) + s; else s = (char) ((b % a) + '0') + s; b /= a; } return s; }}
Вывод: в ходе лабораторной работы были изучены способы изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения.
Ответы на контрольные вопросы:
Система счисления – это символический метод записи чисел, представление чисел с помощью письменных знаков.
Чтобы перевести целое число из одной позиционной системы счисления в другую необходимо исходное число последовательно делить на основание новой системы счисления, записанное в исходной системе счисления, до получения частного, равного нулю. Число в новой системе счисления записывается из остатков от деления, начиная с последнего. Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основание той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Если основание системы счисления q кратно степени двойки (q = 2n), то любое число в этой системе счисления можно «быстро» перевести в двоичную систему счисления, выписав последовательно двоичные коды каждой из цифр, образующих исходное число. Замена восьмеричных цифр двоичными тройками и шестнадцатеричных цифр двоичными четвёрками позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
При представлении с плавающей запятой размещение десятичной точки может ‘плавать’ относительно значащих цифр числа. Например, представление с фиксированной точкой с равномерным размещением десятичной точки может представлять числа 123.45, 1234.56, 12345.67 и т.д., Тогда как представление с плавающей точкой может дополнительно представлять 1.234567, 123456.7
Чтобы поместить в 16 бит число со знаком и фиксированной точкой, надо:
1) старший бит отвести под знак
2) оставшиеся 15 бит поделить между целой и дробной частями так, чтобы в целую поместилось число 791<2¹⁰.
В итоге (слева направо): бит под знак, 10 бит под целую часть, пять - под дробную.
Такой метод является компромиссом между точностью и диапазоном представляемых значений. Представление чисел с плавающей точкой рассмотрим на примере чисел двойной точности (double precision). Такие числа занимают в памяти два машинных слова (8 байт на 32-битных системах). Наиболее распространенное представление описано в стандарте IEEE 754.
Кроме чисел двойной точности также используются следующие форматы чисел:
половинной точности (half precision) (16 бит),
одинарной точности (single precision) (32 бита),
четверной точности (quadruple precision) (128 бит),
расширенной точности (extended precision) (80 бит).
Форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода. Таким образом, каждая тетрада двоично-десятичного числа может принимать значения от 0000₂ до 1001₂.
ASCII (American Standard Code for Information Interchange – Стандартный американский код обмена информацией) – это код для представления символов в виде чисел, в котором каждому символу сопоставлено число от 0 до 127.
Юникод (Unicode), это многоязычный, основанный на ASCII стандарт кодирования символов, а также, связанное с ним, семейство многобайтных кодировок.
Сложение выполняется просто, если представить в уме, что мы должны сложить две десятичные дроби «в столбик» на листе бумаги. При выполнении данной операции числа записываются в столбик так, чтобы запятые, отделяющие дробную часть, располагались одна под другой. В двоичной арифметике подобная операция называется приведением экспонент.При сложение с плавающей точкой нужно сделать выравнивание порядка, а затем сложить мантису.
