Семестр6 / ТАК / Матеріали / 2

1. Структурна стійкість

Існують структурно нестійкі системи, які не можуть стати стійкими при жодних комбінаціях їх значень та параметрів. Структурно стійкішими звуться такі системи, які при певних значень їх параметрів можуть стати стійкими. За видом структурної схеми можна визначити чи є система стійкою, або нестійкою.

Розглянемо деякі випадки. Для цього введемо деякі нові типи ланок:

1. Нестійка інерційна ланка

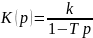
2. Нестійка коливальна ланка

Якщо в одноконтурній системі міститься ідеальні інтегральні ланки, то знаменних передаточної функції розімкнутої системи містить множник p. Отже знаменник має корені, які розташовані на границі стійкості.

За допомогою критерій стійкості Михайлова можна довести, що одно контурна система послідовно встановлених аперіодичних, коливальних та ідеально інтегрувальних ланок буде після замикання структурно нестійкою:

1. Якщо вона містить більше однієї ідеальної інтегрувальної ланки, то система буде нестійка, або нестійкої інерційної ланки.

2. Якщо кількість нестійких коливальних (консервативних) ланок в ній r така, що степінь n характеристичного рівняння не більше ніж 4r( ).

3. Якщо система містить 1-ну ідеальну інтегральну і 1-ну нестійку інерційну ланку.

Припустимо, що розімкнута система мітить q ідеально – інтегрувальних ланок, решта – аперіодичні та коливальні періодичні функції.

Характеристичне рівняння замкнутої системи

Розглянемо годограф Михайлова,якщо q=1, то коефіцієнт підсилення æ=0.

При , .

Якщо збільшити , то також збільшується і аргумент монотонності збільшується. Система стійка.

П ри збільшенні коефіцієнта підсилення годограф Михайлова зсувається праворуч і система стає стійкою.

q=1; æ=0

Аргумент починає збільшуватися від початкового зсуву П, жодним зсувати праворуч не вдається задовольнити критерій стійкості Михайлова.

А налогічно доводиться, що одно контурна система, яка містить одну нестійку інерційну і одну ідеально інтегральну ланку,а також будь – яке число інтегралу також (більше за 1) буде структурно нестійка.

Нехай у системі є аперіодична ланка з передаточною функцією та консервативна ланка з передаточною функцією , тоді характеристичне рівняння замкнутою системи буде:

, тому неможливо задовольнити умовам стійкості при жодних , а відтак така система структурно нестійка.

Якщо система багатоконтурна, щоб застосувати наведені правила потрібно її привести за допомогою структурних перетворень до одноконтурної.

2. Визначити стійкість. Критерій Михайлова. Робоче формулювання:

Для того, щоб САК, яка має характеристичне рівняння n – ого порядку (n=4) була стійкою, необхідно і достатньо, щоб годограф Михайлова почався на додатковій дійсній вісі комплексної величини і проходить послідовно n квадратів цієї площини у додатному напрямі (проти руху годинникової стрілки).

Зробити заміну

Виділимо дійсну та уявну частоту:

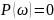
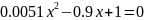
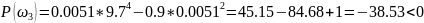
П обудуємо годограф Михайлова

Оскільки годограф Михайлова почався на додатній вісі комплексної величини і пройшов послідовно 4 квадрати усієї площини у додатному напрямі то дана система є стійкою.

Передаточна функція за помилкою:

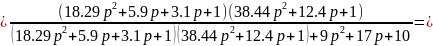
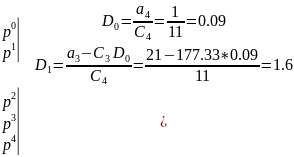
Якщо підвищити коефіцієнт підсилення у 10 разів

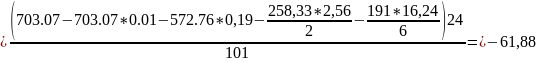
Порівнюючи коефіцієнти помилок в обох випадках ми бачимо, що коефіцієнт при збільшеному коефіцієнту підсилення мають значення на порядок нижчі. Тобто більш точніші, але зменшуються запаси стійкості.

2 . Під регулятор

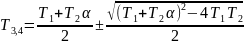
Характеристика ПІД регулятора

Характеристики ПІД регулятора у вигляді послідовного коректувального пристрою в САК.

1. ЛАЧХ ПІД регулятора

2. ЛАЧХ незмінної частини без ПІД регулятора

3. ЛАЧХ САК з викор ПІД регулятора

4. Кінцево – скорегована система з ПІД регулятором

1. ЛФЧХ ПІД регулятора

2. ЛФЧХ незмінної системи буз корегування

3. ЛФЧХ скорегованої системи за допомогою послідовно коректувального ПІД регулятора

Порівнюючи ЛФЧХ вихідної та скорегованої системи можна сказати, що послідовний регулювальний ПІД регулятор знано може збільшити коефіцієнт підсилення та збільшити її частоту зрізу, тобто збільшити точність як в установленому, так й в перехідному режимі та її швидкодійності.