41. Распределение и криптографическая защита в протоколе tls/ ssl.

Протокол Transport Layer Security (TLS), который является более современной версией Secure Sockets Layer (SSL), обеспечивает безопасное установление защищенного канала связи между клиентом и сервером на уровне транспортного уровня для обеспечения конфиденциальности, целостности данных и аутентификации участников. В TLS/SSL используются различные методы для распределения ключей и криптографической защиты.

Распределение ключей в протоколе TLS/SSL:

• Симметричное шифрование: При установлении безопасного канала клиент и сервер договариваются об использовании общего секретного ключа для шифрования и дешифрования данных. Этот секретный ключ обычно получается путем обмена открытыми ключами и договоренности секретного симметричного ключа.

• Асимметричное шифрование: В процессе подтверждения подлинности и установления секретного канала, используются асимметричные ключи для зашифрования информации о согласовании симметричного ключа и другой критической информации.

Криптографическая защита в протоколе TLS/SSL:

• Шифрование: Данные, передаваемые по защищенному каналу, шифруются для предотвращения прослушивания и несанкционированного доступа к информации.

• Цифровые подписи: Подписи используются для аутентификации данных и гарантии, что полученные данные были отправлены известным и доверенным источником.

• Хеширование: Используется для обеспечения целостности данных, чтобы убедиться, что данные не были изменены во время передачи.

• Аутентификация: TLS/SSL обеспечивает аутентификацию клиента и сервера, чтобы обеспечить доверие между сторонами.

Процесс работы TLS/SSL для обеспечения безопасности:

1. Установление соединения: Клиент и сервер обмениваются сведениями о версии протокола, алгоритмах шифрования и другой критической информации для установления безопасного канала.

2. Аутентификация: Проверка подлинности сервера и, при необходимости, клиента.

3. Установление секретного ключа: Договоренность о симметричном ключе для шифрования и дешифрования данных.

4. Обмен данных: Защищенный обмен информацией между клиентом и сервером через безопасный канал.

5. Завершение соединения: Подтверждение завершения обмена данных и безопасное завершение соединения.

А теперь мы переходим к практике…

1. Построить систему электронного голосования на основе крипто системы Пэйе. (Число избирателей N_v= X, число кандидатов 3, остальные параметры выбрать самостоятельно, b=6)

Ебать Тысяча чертей. А как это на экзамене писать и считать?..

2. Показать выполнение свойств гомоморфизма в системе шифрования Пэйе на примере р=7, q= 5.

Модуль n = pq = 7 * 5 = 35.

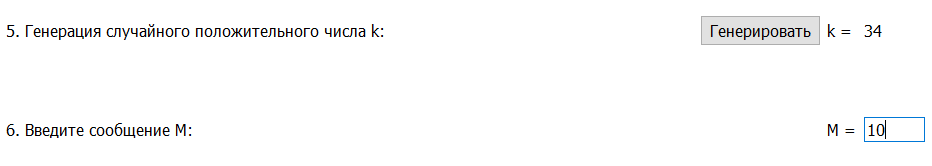
Сообщение m = 10, r = 6.

c = (g^m * kⁿ) mod n² = (29¹⁰ * 34³⁵) mod 35^{2 = 699}

^{P(m)r mod n2 = 699^6 mod 35^2 = 701}

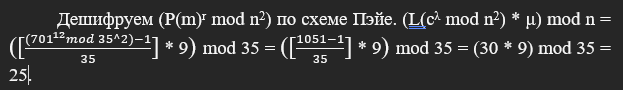
^{m1 = 12, m2 = 17.}

^{c1 = (g^m1 * k^n) mod n^2 = (29^12 * 34^35) mod 35^2 = 1084}

^{c2 = (g^m2 * k^n) mod n^2 = (29^17 * 34^35) mod 35^2 = 1091}

^{c = (P(m1) * P(m2)) mod 35^2 = (1084 * 1091) mod 35^2 = 519}

^{3. Показать выполнение свойств гомоморфизма в системе шифрования Эль Гамаля на примере р=11, g= 5.}

^{Первое свойство (мультипликативное). КС Эль-Гамаля гомоморфна относительно операции перемножения открытых сообщений.}

^{M1 = 6, M2 = 7.}

^{(6 * 7) mod 11 = 42 mod 11 = 9 - произведение открытых сообщений.}

^{Шифрование:}

^{Выбираем случайное целое число a (1 < a < p) = 8.}

^{g^a mod p = 5^8 mod 11 = 4.}

^{Открытый ключ = (11, 5, 4).}

^{Закрытый ключ = 8.}

^{Сессионный ключ k (1 < k < p - 1) = 7, k взаимно простое с p - 1.}

^{𝛾 = g^k mod p = 5^7 mod 11 = 3}

^{𝛿1 = (g^a mod p)^k * M1 mod p = 8}

^{C1 = (3, 8), (11, 5, 4).}

^{𝛿2 = (g^a mod p)^k * M2 mod p = 2}

^{C2 = (3, 2), (11, 5, 4).}

^{Произведение криптограмм C1 * C2 = (3*3, 8*2) = (9, 5).}

^{Расшифруем произведение криптограмм: M = 𝛿 * 𝛾^(p - 1 - a) mod p = 5 * 9^2 mod 11 = 9.}

^{9 = 9 - верно, расшифрованное произведение криптограмм равно произведению сообщений по модулю p.}

^{Второе свойство (аддитивное). КС Эль-Гамаля гомоморфна относительно операции сложения открытых сообщений.}

^{M1 = 6, M2 = 7.}

^{M1 + M2 mod 11 = 13 mod 11 = 2 - сумма открытых сообщений.}

^{Выберем b = 8 (M < b < p).}

^{1 ≤ 𝑘 ≤ 𝑝 − 2, k = 7.}

^{1 ≤ 𝑎 ≤ 𝑝 − 2, a = 8.}

^{𝛾 = 𝑔^𝑘 𝑚𝑜𝑑 𝑝 = 5^7 mod 11 = 3}

^{𝛿1 = 𝑏^𝑀1 * 𝑔^(𝑎*𝑘) 𝑚𝑜𝑑 𝑝 = 4}

^{C1 = (3, 4)}

^{𝛿2 = 𝑏^𝑀2 * 𝑔^(𝑎*𝑘) 𝑚𝑜𝑑 𝑝 = 9}

^{C2 = (3, 9)}

^{Произведение криптограмм: C1 * C2 = (3 * 3, 4 * 9) = (9, 36)}

^{logb (b^(M1+M2)) = log8 (8^13) = 13.}

^{13 mod 11 = 2.}

^{Получившееся число равно сумме открытых сообщений. Второе свойство выполняется.}

^{4. Найти период хуйкции a^x mod n, n = 7*x, испольхуя квантовый сихулятор.}

^{Возьмём a = 3.}

xуй	10^x mod n, n = 7*x
0	10^0 mod 0 = tf n1994 (0?)
1	10^1 mod 7 = 3
2 (The Money Shop)	10^2 mod 14 = 4
3	10^3 mod 21 = 18
4	10^4 mod 28 = 16
5	10^5 mod 35 = 25
6	10^6 mod 42 = 6
7	10^7 mod 49 = 21
8	10^8 mod 56 = 16
9	10^9 mod 63 = 54
10

^{a = 7, n даст на экзамене.}

^{Просто считаешь функцию, пока значения не начнут повторяться.}

^{5. На квантовом симуляторе получено значение периода 6, M=35, найти множители p, q.}

^{Период r = 6.}

^{Выберем число а, взаимно простое с M. а = 3.}

^{k = r/2 = 3.}

^{q = НОД(3^3 - 1, 35) = НОД(8, 35) = 1}

^{p = НОД(3^3 + 1, 35) = НОД(10, 35) = 5}

^{Если одно из чисел 1, то находим его через второе:}

^{q = M/p = 35/5 = 7}

^{Проверка: p*q = 7*5 = 35 = M - множители числа М найдены верно.}

^{6. Расшифровать криптограмму в КС Рабина С=28?. p=11, q=31.}

^{Моё любимое число - 28?}

^{7. Атака Винера. Условие n=569319797, e=1626?8823. Найти d.}

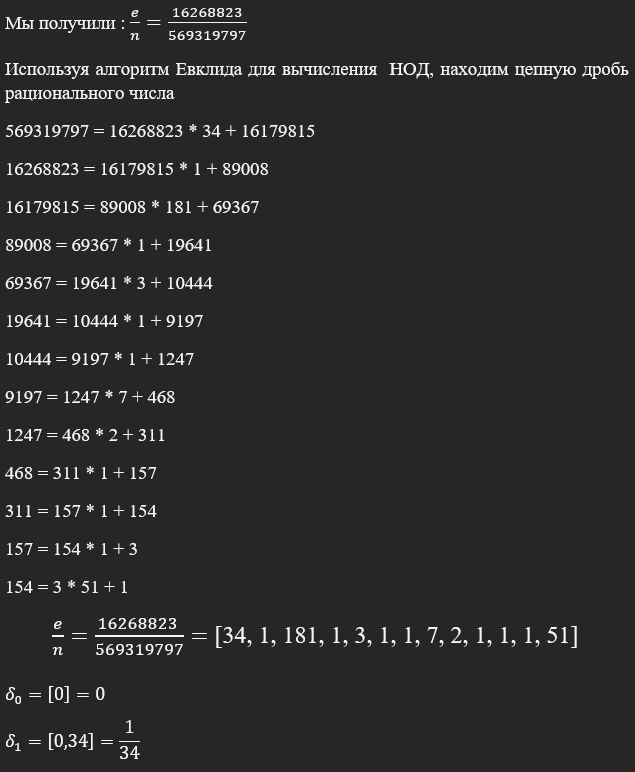
^{8. Решить уравнение при p = 23.}

^{p = 4k + 3}

Например, a = 3.

x^2 = a^(24/4) mod 23 = 3^6 mod 23 = 16.

x = +- 4

^{9. Решить уравнение при p = 17.}

^{a = 7.}

^{p = 4k + 1. Алгоритм Чиполлы.}

^{Посмотреть, чтобы a^((p-1)/2) = 1. Я забыл про это, но алгоритм такой же.}

^{Подбираем b пока не будет достигнуто равенство .}

^{b = 6.}

^{10. Решить уравнение при p = 21.}

^{То же самое, что в пункте 9 (p = 4k + 1).}

^{11. Проверить тестом Ферма является ли число а= ? простым. Вероятность ошибки не более 0,2.}

^{Возьмём а = 17. По идее, кстати, должно быть дано p, потому что а - это “свидетели”, по которым мы проверяем простоту.}

^{Чтобы вероятность ошибки (½)^k была не более 0,2, возьмём k = 3 (вероятность ошибки 0,125).}

^{Простые числа 3, 5, 7.}

^{a^(p-1) mod p. Если в большинстве случаев равно 1, то число, скорее всего, простое.}

^{3^16 mod 17 = 1}

^{5^16 mod 17 = 1}

^{7^16 mod 17 = 1}

^{Число 17 простое (вероятность ошибки не более 0,125).}

12. Проверить тестом Рабина-Миллера является ли число n=? простым. Вероятность ошибки не более 0,05.

Пусть n будет 561.

1. n-1 = m*2^r (согласно теореме)

560 = 35 * 2⁴ (находим m и r)

2. Выбираем случайное число a, такое, что

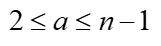
a = 2

3. Вычисляем y₀ = a^r mod n

3.1) y₀ = 2³⁵ mod 561 = 263 (продолжаем тест)

3.2) y₁ = 263² mod 561 = 166 (продолжаем тест)

3.3) y₂ = 166² mod 561 = 67 (продолжаем тест)

3.4) y₃ = 67² mod 561 = 1 (число составное)