Алгоритм Дойча (алгоритм параллельных вычислений)
• Рассмотрим булеву функцию от одной переменной
• f (x) :{0,1} {0,1}
Существует всего 4 таких функций:
|
|
x |
f1 |
f2 |
f3 |
f4 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
• |
|
1 |
0 |
1 |
1 |
0 |
4 |
|
|
|
|
|
|
||
Первые две функции – функции константы, 3 и |
|||||||
функции не константы. Чтобы определить тип функции, нужно в классической системе сделать два запроса на вычисления. При квантовых вычислениях – только один.
12
Решение
Запишем состояния 0 и1 кубита
q 0 |
|
0 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 1 |
|
0 |
0 |
1 |
или |
|
0 |
|
|
1 |
|
|||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 0 |
|
0 |
1 |
1 |
или |
|
1 |
|
0 |
|
|
|||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сначала возьмем систему из одного кубита в базисном состоянии, соответствующем логическому нулю.
К полученному кубиту применяем преобразование Адамара
H1 |
|
1 |
|
1 |
1 |
|
|
|
1 |
|
|||
2 |
||||||
|
|
|
1 |
13
Построение матриц Адамара
H0 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
Hn 1 |
|
|
Hn 1 |
|
|
|||||||||||
Hn |
1 |
|
Hn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
Hn 1 |
|
Hn 1 |
|
|
||||||||||||
|
|
|
|
1 |
1 |
|
|
1 |
1 |
|
|
||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|||||||||
|
|
|
|
1 |
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
1 |
1 |
|
H2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
H1 |
|
|
|
1 |
1 |
|
|
1 |
|
1 |
|||||||||
|
|
|
|
||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
|
1 |
1 |
|
|
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
||||||||||||||||
14
H |
|
0 |
|
1 |
1 |
1 |
1 |
|
|
1 |
|
1 |
|
1 |
( |
|
0 |
|
1 ) |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
1 |
1 |
0 |
|
|
2 |
|
1 |
|
2 |
|
|
|
|
|
Это λi
• Далее выполняем еще одно преобразование, которое называется фазовый запрос Of
Of H |
|
0 |
|
1 |
|
( 1) f (0) |
0 |
|
|
1 |
|
1 |
|
( 1) f (0) |
|
1 |
(( 1) f (0) |
|
0 |
( 1) f (1) |
|
1 ) |
||
|
|
|
|
|||||||||||||||||||||
|
|
|
0 |
( 1) |
f (1) |
|
|
|
|
( 1) |
f (1) |
|
|
|
|
|||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
•Далее еще раз применяем преобразование Адамара.
HOf H |
|
0 |
|
1 |
|
1 |
1 |
( 1) f (0) |
|
( 1) f (0) ( 1) f (1) |
|
0 |
( 1) f (0) ( 1) f (1) |
|
1 |
||
|
|
|
|||||||||||||||
|
2 |
|
1 |
|
( 1) |
f (1) |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
15
x |
f1 |
f2 |
f3 |
f4 |
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
• Таким образом после этих преобразований мы получаем суперпозицию состояний с амплитудами
|
( 1) f (0) ( 1) f (1) |
, |
( 1) f (0) ( 1) f (1) |
||||||||
0 |
|
2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
получаем |
||
• Для функции типа константы |
|
|
|
|
|
|
|
|
|||
амплитуды |
|
и измерение конечного |
|||||||||
|
|
|
f (0) |
f |
(1) |
|
|||||
состояния с вероятностью |
|
|
|
|
|
|
|
определит, |
|||
0 1, 1 |
0 |
|
|
|
|
|
|
|
|
|
|
что система находится в состоянии |
0 |
|
2 |
1 |
. |
|
|||||
|
|
||||||||||
|
|
P |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
16
• |
Для функции, не являющейся константой |
||||||||
f (0) f (1) амплитуды равны |
0 0, 1 1 |
||||||||
и с вероятностью |
P |
|
1 |
|
2 получим состояние |
||||
|
|
||||||||
|
. |
|
|
|
|
1 |
|
||
• |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Таким образом в процесс только одного |
|||||||||
|
измерения мы получаем результат , |
||||||||
который означает, что функция |
является |
||||||||
|
|
|
|
|
|
|
|
|
f (x) |
|
константой или не константой в противном |
||||||||
случае.
17
Алгоритм Дойча-Джоза
• Обобщает алгоритм Дойча на случай функции n
переменных |
0 |
1 |
n 1 |
) : |
|
|
n |
|
|
|
|
||||||||||
|
|
|||||||||
|
f (x |
, x |
, , x |
|
0,1 |
|
|
0,1 |
•Позволяет определить за одно измерение является ли функция константой или сбалансированной функцией , т.е. если в половине случаев она принимает значение 0, а в другой половине 1.
• Амплитуда |
принимает значение |
|
если функция константа и 0, если она |
1 |
|
сбалансирована. |
|
|
0 |
|
|
18
Алгоритм ускоренного поиска (алгоритм Гровера)
Рассмотрим решение уравнения |
|
|
, где функция f(x) принимает |
||||||||
значения{0,1}, |
|
|
|
|
f (x) 1 |
||||||
|
|
|
|
|
|
||||||
но только при одном значении. |
|
|
|
|
|
||||||
Состояние системы в общем виде можно записать так |
|||||||||||
|
|
|
f (xi ) |
1, |
f (x j ) |
0, j i |
|||||
Где |
амплитуда i-го состояния. |
|
|
|
|
|
|
||||
|
2n 1 |
|
|
|
|
|
|
||||
|
i |
|
xi 0 |
|
x0 |
1 |
|
x1 |
2n 1 |
x2n 1 |
|
|
|
|
|
||||||||
|
|
|
|
||||||||
|
i 0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
i
19
•Идея алгоритма Гровера состоит в том, чтобы увеличить, например, │λx0│ за счет других │λx│.
•Этого можно добиться k кратным преобразованием диффузии.
[ψ>=DD…D[ψ1>,
где [ψ1> – начальный вектор состояния, D – матрица преобразования.
20
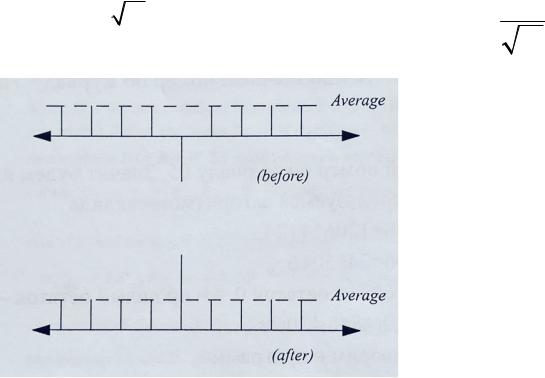
Математическое преобразование - инверсия относительно среднего (ИОС)
Пусть задан вектор v v1,v2 , ,vN |
каждая координата которого |
||||
v |
1 |
i=1,2,…,N , i x |
|
1 |
|
N |
vx |
||||
i |
|||||
|
|
|
|
||
N
vx
V’x
Пусть |
а |
1 |
vi - среднее значение. |
|
N |
||||
|
|
i |
Изменим состояние вектора
vi vi 2a a (a vi )
Это и есть инверсия относительно среднего
Пример. N=16, vi=1/4. vx=-1/4.
Находим а=14/64. тогда vi 6 / 32 2 /10
vx 22 / 32 7 /10