Лекция 4
Стойкость криптоалгоритмов в условиях атак с использованием квантового
компьютера 1.Принципы квантовых вычислений. 2.Алгоритм ускоренного поиска Гровера.
3.Алгоритм факторизации числа на квантовом компьютере Питера Шора
1
Понятие о квантовых вычислениях
•В классических ЭВМ бит задается ячейками с двумя устойчивыми состояниями: триггер, конденсатор, магнитный домен…Одно из этих состояний условно обозначается 0, другое 1.
•Для хранения нескольких бит используются регистры как совокупность ячеек для хранения бит
1 |
2 |
3 |
|
n-1 |
n |
Для хранения 2n чисел |
|
1 |
0 |
1 |
|
0 |
|
1 |
нужно 2n регистров |
|
|
|
|||||
|
|
|
|
|
|
|
|
2
•В квантовом компьютере бит это квантовая система с двумя возможными физическими состояниями элементарной частицы: спин электрона в магнитном поле, энергетический уровень атома водорода, две поляризации фотона.
•Математическая модель состояния частицы описывается вектором в 2-х мерном пространстве:
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
||
где |
, |
- состояния системы, а |
|
|
- комплексные амплитуды состояния. |
|
|
||
Соотношение (1) называетcя квантовым битом или q-битом. |
|
|
|||||||
|
|||||||||
|
|
|
|
0 0 |
1 |
1 |
|
|
|
Квадраты |
модулей являются вероятностями обнаружения частицы в |
||||||||
|
0 |
1 |
|
|
, |
|
0 и 1 |
||
соответствующих состояниях: |
|
||||||||
|
|
|
|
||||||
при измерении .
Состояние частицы выясняется только после измерения, а текущее (скрытое) состояние представляет собой линейную смесь (1).
0
1
02 12 1
3
Обозначения
Состояние кубита |
|
x |
|
0 |
|
|
0 1 |
|
1 принято |
||||||
|
|
|
|||||||||||||
обозначать |
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
Или вектор-столбцом |
|
- кет-вектор, |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
Или вектор-строкой |
|
0 |
1 - бра-вектор |
||||||||||||
|
0 |
|
1 |
|
, |
|
1 |
|
0 |
|
. |
|
|
||
|
|
|
|
||||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
4
n- кубитовый регистр
1 |
2 |
3 |
|
n-1 |
n |
|
|
|
|
|
|
|
|
|
В одном регистре сразу |
▪▫ |
▫▪ |
▪▫ |
|
▫▪ |
|
▪▫ |
|
|
|
может быть 2n возможных чисел |
|||||
|
|
|
|
|
|
|
|
С увеличением числа ячеек в регистре состояния частиц оказываются взаимосвязанными (сцепленными). Например система из 2-х кубитов может находиться в состоянии
λ00│00>+ λ01│01>+ λ10│10>+ λ11│11>
При обобщении на n-кубитовый регистр по аналогии описывается линейной
комбинацией.:
2n 1
x x
x 0
где |
|
x |
|
00 01 |
- состояние регистра |
|
|
||||
|
|
|
|
|
|
5
Вычисление функции в кубитовом регистре
Пусть задана функция f(x), преобразующая n-разрядное число x в m-разрядное число f(x). Для описания функции можно построить таблицу
x |
f(x) |
|
|
|
|
00000 |
001 |
|
|
|
|
00001 |
010 |
2n строк |
|
|
|
… |
… |
|
|
|
|
11111 |
110 |
|
|
|
|
В квантовом компьютере достаточно лишь один раз выполнить преобразование f(х) исходного регистра из n ячеек, где содержатся все n-разрядные числа x и получить все значения функции.
Для ее записи нужно иметь m ячеек памяти Всего нужно иметь n+m кубитых ячеек..
7
x 2
8
Идея квантовых вычислений
• Принцип квантовых вычислений заключен в увеличении модуля комплексных амплитуд │λx0│тех состояний x0 , f (x)
, которые хотелось бы получить в результате считывания.
•Процесс вычисления – последовательность унитарных преобразований ненаблюдаемого состояния регистра.
Унитарное преобразование задается унитарной матрицей - Н. Матрица Называется унитарной , еслиH H где - комплексно сопряженная матриц Этим обеспечивается обратимость преобразования.
Для обратимых преобразований выполняется условие нормировки
02 12 1
9
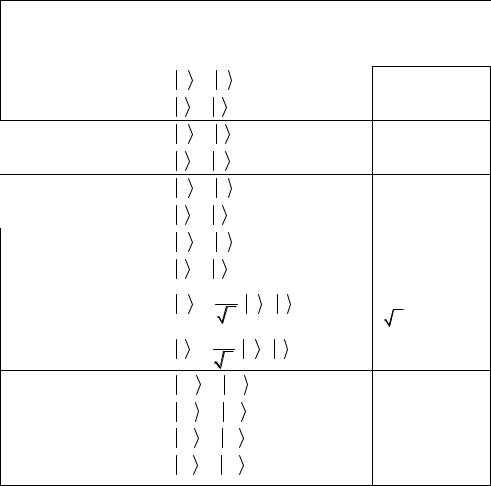
Элементарные преобразования
Нaзвание и |
Результат |
обозначение |
преобразования |
Тождественное
преобразование II
Отрицание X
Фазовый сдвиг -Z
Фазовый сдвиг
с отрицанием Y
Преобразование
Адамара Н
CNOT
Прибавление ко второму биту первого
mod2
0 |
0 |
|
|
|
1 |
1 |
|
|
|
0 |
1 |
|
|
|
1 |
0 |
|
|
|
0 |
0 |
|
|
|
1 |
1 |
|
|
|
0 |
0 |
|
|
|
1 |
1 |
|
|
|
0 |
|
1 |
( 0 |
1 ) |
|
|
2 |
|
|
1 |
|
1 |
( 0 |
1 ) |
|
|
2 |
|
|
00 |
00 |
01 |
01 |
10 |
11 |
11 |
10 |
Матрица 
1 |
|
0 |
|
||
|
0 |
|
1 |
|
|
|
|
|
|
||
0 |
|
1 |
|
||
|
1 |
|
0 |
|
|
|
|
|
|
||
1 |
|
0 |
|||
|
0 |
|
|
|
|
|
|
1 |
|||
|
0 |
|
1 |
|
|
|
1 |
0 |
|
||
|
|
||||
|
1 |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
2 |
|
|||
|
|
|
1 |
||
1 |
0 |
0 |
0 |
||
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
||||
|
0 |
0 |
1 |
0 |
|
10
Задачи, решаемые с помощью квантового компьютера
•Проверка является ли булева функция константой
– алгоритм Дойча-Джоза.
•Задача поиска решения уравнения f (x) 1 , где функция принимает значения (0,1) – алгоритм Гровера.
•Квантовое преобразование Фурье.
•Задача факторизации числа – алгоритм Шора.
•Задача дискретного логарифмирования-алгоритм Шора
11