9_2 9_3

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №9.2-9.3

«Криптографические протоколы проверяемого разделения секрета» (тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Выполнил студент 3 курса:

Травкина Е.А., ИКБ-14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д.т.н., проф. Яковлев В.А.

(Ф.И.О., № группы) (подпись)

Цель лабораторной работы: закрепление теоретических знаний студентов по криптографическим протоколам разделения секрета и изучения схем проверяемого разделения секрета Фельдмана и Педерсена.

Таблица 1. Вариант задания 19

Номер варианта	Параметры k, n	p, q	Секрет s	g
19	4, 5	103, 17	14	72

Лабораторная работа 9-2

Исследование схемы проверяемого разделения секрета Фельдмана

Дилером выбраны p = 103, q = 17

Проверка: (p – 1) mod q = 0 → (103 – 1) mod 17 = 0 → числа p и q подходят.

g = 72

Проверка: g^q mod p = 1 → 72¹⁷ mod 103 = 1 → число g подходит.

Секрет s = 14, а коэффициенты многочлена Q(x):

Q₀ = s = 14, Q₁ = 5, Q₂ = 9, Q₃ = 9

Дилер выбирает полином: Q(x) = 9x³ + 9x²+5x + 14.

Дилер вычисляет проверочные значения, которые будут раздаваться всем участникам разделения g^q mod p:

g^q mod p = 72¹⁴ mod 103 = 30

g^q mod p = 72⁵ mod 103 = 5

g^q mod p = 72⁹ mod 103 = 81

g^q mod p = 72⁹ mod 103 = 81

Частные тени вычисляются по формуле s_i = Q (x_i) mod q:

s₁ = Q (x₁) = (9*1³ + 9*1²+ 5*1 + 14) mod 17 = 3

s₂ = Q (x₂) = (9*2³ + 9*2²+ 5*2 + 14) mod 17 = 13

s₃ = Q (x₃) = (9*3³ + 9*3²+ 5*3 + 14) mod 17 = 13

s₄ = Q (x₄) = (9*4³ + 9*4²+ 5*4 + 14) mod 17 = 6

s₅ = Q (x₅) = (9*5³ + 9*5²+ 5*5 + 14) mod 17 = 12

Убедимся с помощью программы, что вычисления выполнены верно (Рис. 1)

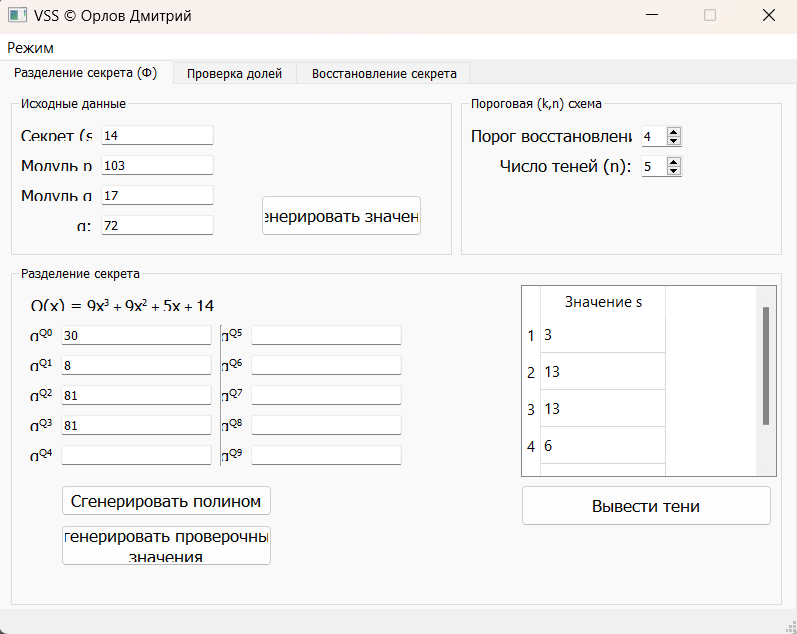
Рисунок 1. Проверка вычислений

Проверка долей

Проверочное уравнение имеет вид: .

Пусть второй участник решил проверить свою долю. Тогда уравнение будет иметь следующий вид:

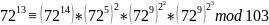
9 = 9 → проверка успешно пройдена, убедимся в этом с помощью программы (Рис. 2).

Рисунок 2. Проверка вычислений

Восстановление секрета

Восстановим секрет для 1, 2, 3, 4 участников посредством использования интерполяционной функции Лагранжа:

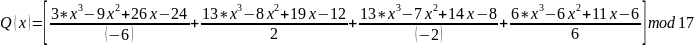= -0,5* + 6,5*( -20 + 30,5 x - 8 x² + 0,5 x³) mod 17 = 14 + 30,5x + 9x² + 0,5x³

Свободный член в полученном полиноме 14 и есть восстановленный основной секрет. Убедимся в этом с помощью программы (Рис. 3)

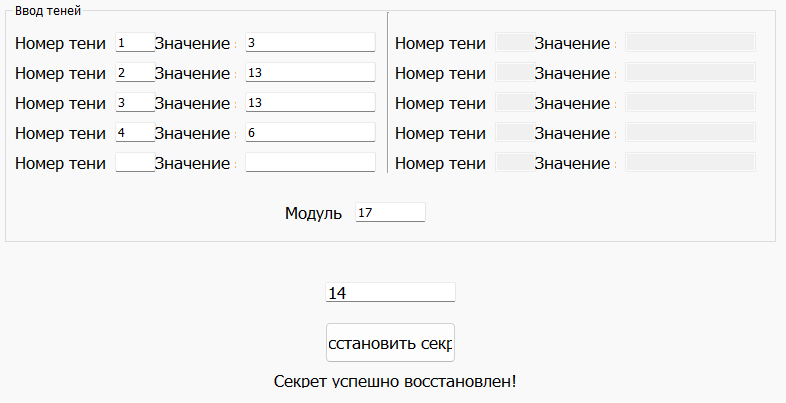
Рисунок 3. Проверка

Лабораторная работа 9-2

Исследование схемы проверяемого разделения секрета Педерсена

Таблица 2. Вариант задания 19

Номер варианта	Параметры k, n	p, q	Секрет s	g
19	4, 5	103, 17	14	72

Числа p, q, g, s определяются так же, как и в схеме Фельдмана.

19 вариант: p = 103, q = 17, g = 72, s = 14

Выбирается – открытое общедоступное число такое, что 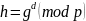, где неизвестно даже дилеру.

Пусть d = 15, тогда h = 72¹⁵ mod 103 = 100

Проверка: 100¹⁷ mod 103 = 1

Чтобы распределить секрет s, дилер выбирает два полинома Q(x) и F(x):

Q(x) = 3x³ + 8x² + 15x + 14

F(x) = 5x³ + 7x² + 12x + 3

И распространяет всем участникам схемы открытую величину :

E₀ = (72¹⁴ * 100³) mod 103 = 14

E₁ = (72¹⁵ * 100¹²) mod 103 = 14

E₂ = (72⁸ * 100⁷) mod 103 = 76

E₃ = (72³ * 100⁵) mod 103 = 64

Затем дилер секретно пересылает всем участникам их доли {s_i, t_i},

где s_i = Q(i), t_i = F(i):

s₁ = Q (1) = (3*1³ + 8*1² + 15*1 + 14) mod 17 = 6

t₁ = F (1) = (5*1³ + 7*1² + 12*1 + 3) mod 17 = 10

s₂ = Q (2) = (3*2³ + 8*2² + 15*2 + 14) mod 17 = 15

t₂ = F (2) = (5*2³ + 7*2² + 12*2 + 3) mod 17 = 10

s₃ = Q (3) = (3*3³ + 8*3² + 15*3 + 14) mod 17 = 8

t₃ = F (3) = (5*3³ + 7*3² + 12*3 + 3) mod 17 = 16

s₄ = Q (4) = (3*4³ + 8*4² + 15*4 + 14) mod 17 = 3

t₄ = F (4) = (5*4³ + 7*4² + 12*4 + 3) mod 17 = 7

s₅ = Q (5) = (3*5³ + 8*5² + 15*5 + 14) mod 17 = 1

t₅ = F (5) = (5*5³ + 7*5² + 12*5 + 3) mod 17 = 13

Убедимся, с помощью программы, что значения вычислены верно (Рис.4):

Рисунок 4. Проверка подсчетов.

Проверка долей

Проверочное уравнение имеет вид:

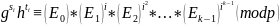
Пусть второй участник решил проверить свою долю. Тогда уравнение будет иметь следующий вид:

Проверка успешно пройдена, убедимся в этом с помощью программы (Рис. 5):

Рисунок 5. Проверка.

Восстановление секрета

Используя интерполяционную формулу Лагранжа:

Восстановим секрет, используя тени пользователей 1, 2, 3, 4:

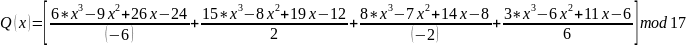= -1* + 7,5*( -37 + 66 x - 26 x² + 3 x³) mod 17 = 14 + 66x +8x² + 3x³

Получили исходный полином, секрет s = Q₀ = 14

Убедимся в правильности восстановления с помощью программы (Рис. 6):

Рисунок 6. Восстановление секрета.

Вывод

В ходе выполнения лабораторной работы были закреплены теоретические знания, а также приобретены навыки использования протокола проверяемого разделения секрета Фельдмана, Педерсена.

Санкт-Петербург

2024