7(доп)

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №7(доп)

Применение методов гомоморфного шифрования для выполнения анонимных вычислений

(Решение неравенства без раскрытия )

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Выполнил студент 3 курса:

Травкина Е.А., ИКБ-14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д.т.н., проф. Яковлев В.А.

(Ф.И.О., № группы) (подпись)

Решение.

1. Пользователи получают ключи по схеме Пэйе:

- открытый ключ и

- закрытый ключ и случайное число – k.

2. Пользователь А шифрует число х1 по схеме Пэйе:

3. Пользователь В шифрует число х2 по схеме Пэйе:

4. Сервер выполняет преобразование зашифрованных данных

где r (r>0) - случайное число и отправляет С пользователям.

5. Пользователи А и В дешифруют С и по свойству гомоморфности получают:

По свойству гомоморфности

6. Тогда, если

если

Дополнительное задание к ЛР7

1. x1=29, x2 брать в одном случае меньше x1, в другом случае больше x1. Выбрать 2. Решить неравенство ,используя криптографическую схему Пэйе и ее гомоморфные свойства.

Ход работы

1. Генерация ключей

x1=№варианта + 10 = 19 +10 = 29

x2 = 20(в первом случае)

x2 = 100 (во втором случае)

Пусть p = 13, q= 17, тогда открытый ключ (n, g) = (221, 4), а закрытый

2. Шифрование

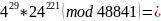= 10054

= 40347 – для первого случая

= 20083 – для второго случая

3. Сервер выполняет преобразование зашифрованных данных

Пусть r = 120;

С = P(x1) * = 10054 * * mod = 13980 – для первого случая

С = P(x1) * = 10054 * * mod =11702 – для второго случая

4. Пользователи А и В дешифруют С, получают:

D(c) = Z= L ( mod = 111 * 37 mod 221 = 129 – для первого случая

L ( mod = = = 111

D(c) = Z = L ( mod = 73 * 37 mod 221 = 49 – для второго случая

L ( mod = = = 73

5. Если Z> n/2, то x1>x2

Если Z <n/2, то x1<x2

Следовательно, в первом случае Z =129>221/2, значит x1>x2; во втором случае Z = 49<221/2, значит x1<x2

Вывод:

В ходе выполнения данной лабораторной работы представлены расчеты по созданию криптосистемы Пэйе и подробное решение неравенства.

Санкт-Петербург

2024