6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

«ИЗУЧЕНИЕ КРИПТОСИСТЕМЫ МАК-ЭЛИС»

(тема отчета)

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Студент:

Травкина Е.А., ИКБ - 14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д-р техн. наук, проф., Яковлев В.А.

(уч. степень, уч. звание, Ф.И.О.) (подпись)

Цель лабораторной работы

Изучить преобразования, выполняемые при шифровании и дешифровании сообщений в системе Мак-Элис, а также простейшие попытки ее взлома.

Ход выполнения лабораторной работы

1. Генерирование порождающей матрицы.

Параметры криптосистемы Мак-Элис:

• длина кодового слова:

• длина информационного сообщения

• число искусственно вводимых ошибок

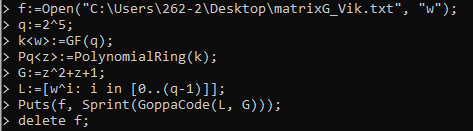
Рисунок 1. Генерирование порождающей матрицы

Рисунок 2. Пример порождающей матрицы.

Параметры кода Гоппы:

• длина

• размерность

• минимальное расстояние

2. Генерация ключей, где – открытый ключ, – закрытый ключ

   1. Генерация порождающей матрицы G.

Рисунок 3. Генерирование порождающей матрицы G

2. Генерация не сингулярной матрицы S.

Рисунок 4. Генерирование не сингулярной матрицы S

3. Генерация перестановочной матрицы P

Рисунок 5. Генерирование перестановочной матрицы P

4. Генерация произведений матриц G*P

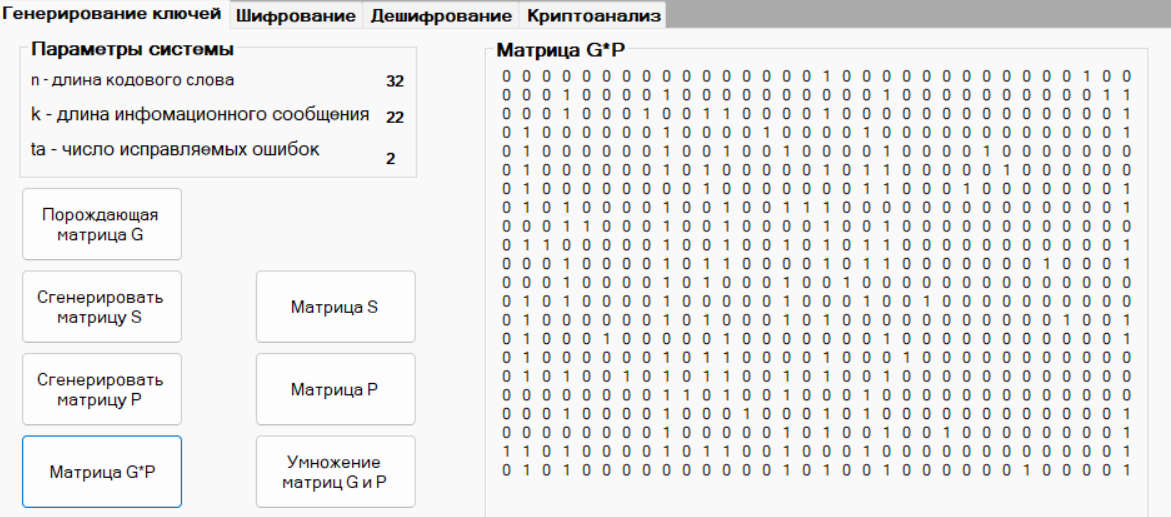
Рисунок 6. Генерирование матрицы G*P

Рисунок 7. Проверка

5. Генерация матрицы

Рисунок 8. Генерирование матрицы

Рисунок 9. Проверка

3. Шифрование сообщения.

Случайное сообщение, содержащее номер варианта 19: 1001100111001101100111 (2519911)

Вектор Z: 00000000000000000000100000000010

Криптограмма: 100010101000011010100001000010000

Рисунок 10. Шифрование сообщения

4. Дешифрование сообщения.

   1. Вычисление вектора , а так же матрицы, обратной P.

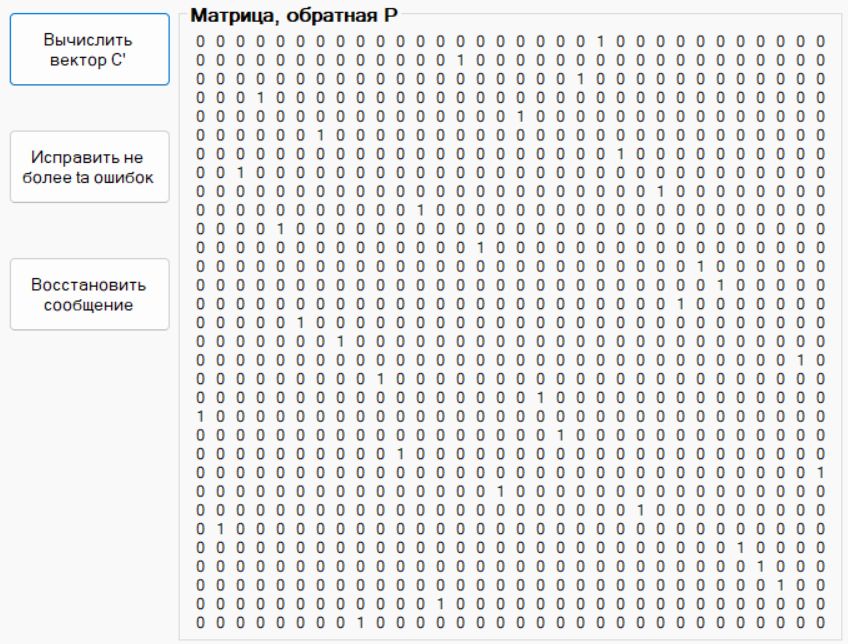
Рисунок 11. Вычисление вектора и обратной матрицы

2. Восстановление сообщения.

Рисунок 12. Восстановление сообщения

Восстановленное сообщение: 1001100111001101100111

Исходное сообщение: 1001100111001101100111

Как видно, расшифрованное сообщение такое же, как и последовательность, зашифрованная ранее.

5. Криптоанализ

Номера столбцов: 15 32 7 20 29 18 30 11 10 6 22 24 26 16 4 25 14 8 23 13 5 3

Нулевой вектор Z: 0000000000000000000000

Восстановленное сообщение: 1001100111001101100111

Рисунок 13. Атака на криптосистему

6. Расчеты вероятности успеха атаки на КС Мас-Элис при выборе различных значений k и t.

Расчет вероятности успеха атаки при длине информационного сообщения k=22, длине кодового слова n=32 (2 ошибки)

Таблица 1. Вероятности успеха при искусственно вводимых ошибках от 1 до 2

k	t
	1	2
22

Из таблицы видно, что при увеличении вводимых ошибок сообщения (от 1 до 2), вероятность успеха снижается.

Вывод:

В ходе выполнения данной лабораторной работы были изучены преобразования, выполняемые при шифровании и дешифровании сообщений в системе Мак-Элис, а также простейшие попытки ее взлома.

Санкт-Петербург

2024