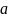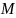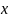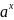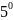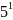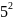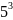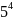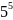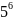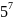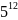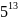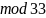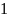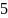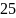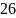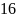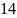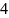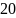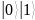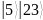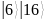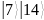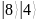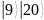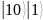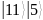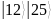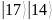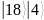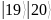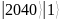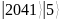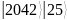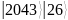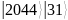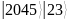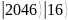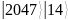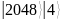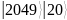5
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
Дисциплина Криптографические протоколы
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5
«ИЗУЧЕНИЕ КВАНТОВОГО АЛГОРИТМА ШОРА ФАКТОРИЗАЦИИ МОДУЛЯ КРИПТОСИСТЕМЫ РША»
(тема отчета)
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Студент:
Травкина Е.А., ИКБ-14
(Ф.И.О., № группы) (подпись)
Преподаватель:
д-р техн. наук, проф., Яковлев В.А.
(уч. степень, уч. звание, Ф.И.О.) (подпись)
Цель лабораторной работы
Ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений, наблюдение принципа работы квантового алгоритма в симуляции. Изучение способа факторизации модуля методом поиска периода для взлома криптосистем РША.
Таблица 1
№ |
|
|
19 |
5 |
33 |
Ход выполнения лабораторной работы
Найти период функции
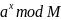 ,
где
,
где
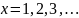 ,
методом простого перебора. Использовать
найденный период для факторизации
модуля. Параметры a
и M
заданы в соответствии с вариантом из
таблицы 1.
,
методом простого перебора. Использовать
найденный период для факторизации
модуля. Параметры a
и M
заданы в соответствии с вариантом из
таблицы 1.
Таблица
1. Функция
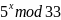
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
23 |
|
|
|
|
|
|
25 |
|
Найденный период: r = 10. Так как число r нечетное, то его можно представить как r = 2k, где k = 5
Следовательно,
с помощью алгоритма Евклида мы можем
найти числа p
и q
как
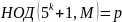 и
и
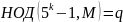 .
.
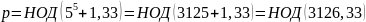 =
3
=
3
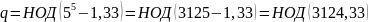 = 11
= 11
Проверяем:
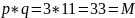
Вывод:
таким образом, была произведена успешная
факторизация модуля
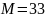 и получено его разложение как
и получено его разложение как
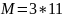
Ознакомиться с квантовой частью алгоритма Шора и выполнить вручную процесс квантового возведения в степень в виде записи состояния регистров для двух периодов. Выбрать любое значение y = 5 и составить для него суперпозицию состояний регистра
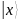 .
.
Для
данного варианта
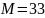 ,
,
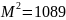 .
Тогда
.
Тогда
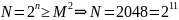 ,
а состояние
,
а состояние
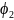 будет иметь вид:
будет иметь вид:
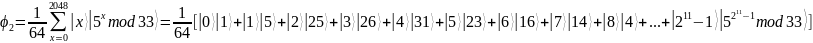 .
.
Тогда
каждому фиксированному состоянию
регистра 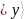
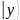 ,
соответствует последовательность
значений регистра
,
соответствует последовательность
значений регистра 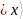 (Таблица 2):
(Таблица 2):
А

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
После
измерения состояния регистра
в соответствии с заданием мы получили
фиксированное состояние
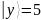 ,
которому соответствует
,
которому соответствует 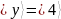 последовательность
значений х
вида:
последовательность
значений х
вида:
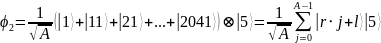 ,
,
где
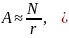 – сдвиг относительно начала координат
(нулевого состояния регистра
,
– сдвиг относительно начала координат
(нулевого состояния регистра
,
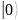 ).
).
Таким
образом, было рассмотрено состояние
регистров на этапе выполнения квантового
возведения в степень и получена
суперпозиция состояний в регистре
,
соответствующих фиксированному состоянию
регистра
–
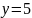 .
.
3. Выполним факторизацию числа М на основе квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe.
Введем в программу модуль M = 33 и факторизуем.
Рассмотрим процесс симуляции выполнения квантового алгоритма Шора для модуля . Можно брать модуль как в соответствии с вариантом, так и произвольный: это должно быть число меньше 100, являющееся произведением двух простых чисел.
Программой
было выбрано целое число
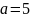 ,
количество кубит, необходимое для
задания размера квантовых регистров
,
количество кубит, необходимое для
задания размера квантовых регистров
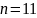 и, соответственно, в этом случае количество
состояний каждого регистра
и, соответственно, в этом случае количество
состояний каждого регистра
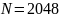 .
.
Проверим:
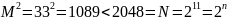 – верное,
– верное,
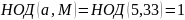 – верное
– верное
Далее пользователю предлагается ознакомиться с процессом выполнения шагов квантового алгоритма Шора и изучить содержание соответствующих вкладок симулятора.
По результатам наблюдения следует сделать выводы:
В
результате выполнения квантового
возведения в степень для функции
для всех состояний регистра
,
в регистре
были получены следующие значения:
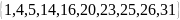 ,
как можно увидеть:
,
как можно увидеть:
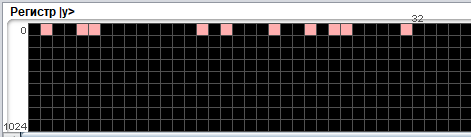
В
результате измерения состояния регистра
было получено фиксированное значение
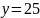 ,
которому соответствует суперпозиция
периодических последовательностей
состояний в регистре
.
,
которому соответствует суперпозиция
периодических последовательностей
состояний в регистре
.
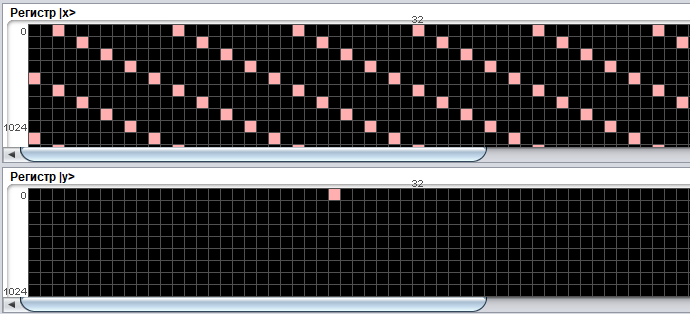
Эта суперпозиция может быть описана как:
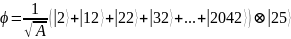 .
.
В результате применения для суперпозиции, содержащейся в регистре , квантового преобразования Фурье, были получены следующие значения (Рис. 6):

Рис.6. - Квантовое преобразование Фурье над регистром
В
результате измерения состояния регистра
из упомянутой выше последовательности
значений было выбрано фиксированное
значение
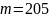 ,
но, как можно увидеть на Рис. 7
,
но, как можно увидеть на Рис. 7
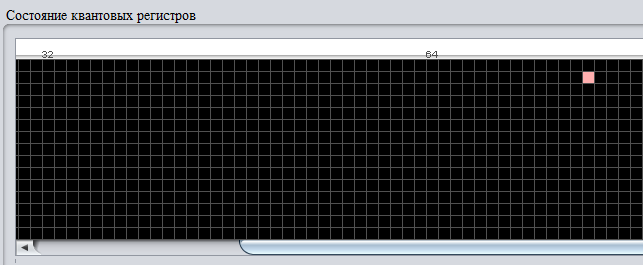
Рис. 7 - Измерение состояния квантового регистра
Дробь
вида
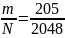 передана на постобработку, которая
выполняется на классическом компьютере.
Произведено разложение непрерывной
дроби
передана на постобработку, которая
выполняется на классическом компьютере.
Произведено разложение непрерывной
дроби
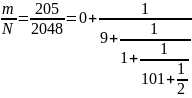 и
получены возможные периоды
и
получены возможные периоды
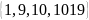 .
Из них условиям, необходимым для
определения периода, удовлетворяет
только
.
Из них условиям, необходимым для
определения периода, удовлетворяет
только
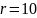 :
:
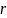 – четное число. Можно убедиться в этом
на рисунке снизу:
– четное число. Можно убедиться в этом
на рисунке снизу:

Найдите подходящие дроби для k=0,1,2,3,4
K |
0 |
1 |
2 |
3 |
4 |
qk |
q=0 |
q=9 |
q=1 |
q=101 |
q=2 |
Pk |
0 |
1 |
1 |
102 |
205 |
Qk |
1 |
9 |
10 |
1019 |
2048 |
На основании полученного значения рассчитаем коэффициенты разложения :
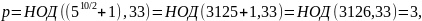
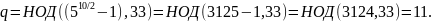
Пробуем вычислить p на основании полученного q: p = M/q = 33/3 = 11
Очевидно,
что факторизация была произведена
успешно. Проверяем:
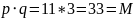 (Рис. 9).
(Рис. 9).

Рис. 9 - Факторизация модуля
Следовательно, значение модуля успешно факторизовано, значит, криптосистема может быть взломана.
Таким образом, был исследован принцип работы квантового алгоритма Шора, рассмотрены отдельные этапы его выполнения и сделаны соответствующие выводы.
Вывод:
 Благодаря
данной лабораторной работе, было
произведено ознакомление с квантовым
алгоритмом факторизации Шора и основами
квантовых вычислений, наблюдение
принципа работы квантового алгоритма
в симуляции, изучение способа факторизации
модуля методом поиска периода для взлома
криптосистем РШ
Благодаря
данной лабораторной работе, было
произведено ознакомление с квантовым
алгоритмом факторизации Шора и основами
квантовых вычислений, наблюдение
принципа работы квантового алгоритма
в симуляции, изучение способа факторизации
модуля методом поиска периода для взлома
криптосистем РШ
Санкт-Петербург
2024