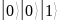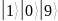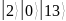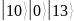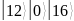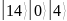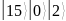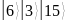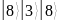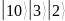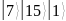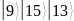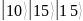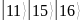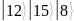5(доп)
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
Дисциплина Криптографические протоколы
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5 (доп)
ИЗУЧЕНИЕ КВАНТОВОГО АЛГОРИТМА ДИСКРЕТНОГО ЛОГАРИФМИРОВАНИЯ ШОРА. АТАКА ВЫЧИСЛЕНИЯ СЕКРЕТНОГО КЛЮЧА КРИПТОСИСТЕМЫ ЭЛЬ-ГАМАЛЯ
(тема отчета)
Направление/специальность подготовки
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Выполнил студент 3 курса:
Травкина Е.А., ИКБ-14
(Ф.И.О., № группы) (подпись)
Преподаватель:
д.т.н., проф. Яковлев В.А.
(Ф.И.О., № группы) (подпись)
Часть 1. Изучение алгоритма дискретного логарифмирования Шора
Исходные данный для дискретного логарифмирования
Таблица 1. Вариант 19
-
№
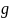
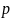
7 (19)
9
2
17
Вручную выполняем расчёт дискретного логарифма. Для этого находим всевозможные значения функции
и записываем их в таблицу.
Таблица 2. Значения функции
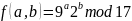
a b |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16
|
17 |
… |
0 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
13 |
16 |
8 |
4 |
2 |
1 |
9 |
… |
1 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
… |
2 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
4 |
2 |
1 |
9 |
13 |
13 |
… |
3 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
… |
4 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
… |
5 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
… |
6 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
… |
7 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
… |
8 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
… |
9 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
… |
10 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
4 |
2 |
1 |
9 |
13 |
13 |
… |
11 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
… |
12 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
… |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
… |
14 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
… |
15 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
… |
16 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
… |
17 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
9 |
13 |
15 |
16 |
8 |
4 |
2 |
1 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.
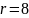Вычислим
дискретный логарифм
используя формулы периодов функции
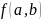для произвольной точки
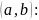
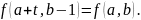
Пусть
,
.
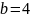Тогда
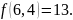
Проверим первое равенство:
Проверим
второе равенство:
Значение
известно и равно 3, а значение
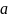равно
.
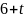То есть интересующая нас ячейка, имеющая
значение 13, находится в 3-й строке и имеет
номер столбца больше 6. Ближайшая ячейка,
удовлетворяющая этому условию – (13, 3).
Действительно,
– второе равенство выполняется.
Таким
образом,
.
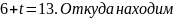
Выполним проверку:
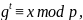
Найденное значение соответствует заданному, следовательно, дискретный логарифм найден верно.
Выполним полуавтоматический расчёт дискретного логарифма с помощью квантового алгоритма Шора, используя для промежуточных вычислений программу QFT.exe.
Определим
необходимое число кубит в регистрах
и
.
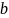Так как период
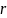функции
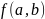равен 8 из условия
.
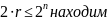
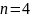То есть число необходимых кубит:
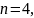число состояний регистра:
.
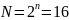Далее вычисляем состояния регистров на разных этапах выполнения алгоритма.
Этап 1.
Установим регистры
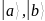и
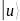в начальное состояние:
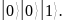
Этап 2. Применим преобразование Адамара к регистрам :
Этап 3.
Применим гейт
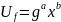к регистру
:
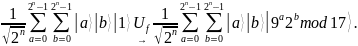
Запишем
состояние регистров
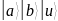в таблицу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что в таблице каждая строка соответствует одному период функции, которая принимает значения 1, 9, 13, 15, 16, 8, 4, 2. Каждый столбец содержит значения и , которым соответствуют одно значение функции.
Этап 4.
Измерим
.
То есть примем за
некоторое конкретное значение
.
Пусть
,
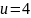тогда:
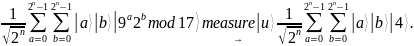
Этому состоянию
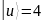соответствует суперпозиция аргументов:
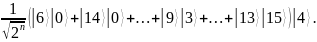
Этап 5. Над полученной периодической суперпозицией в симуляторе КК выполняется обратное квантовое преобразование Фурье:
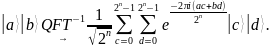
Для выполнения симуляции необходимо запустить программу QFT.exe и выполнить вычисления. Для этого вводим исходные параметры.
Рис. 1. Исходные параметры расчёта
Нажимаем
кнопку Рассчитать. После выполнения
работы программы наблюдаем состояние
регистров до и после обратного квантового
преобразования Фурье. Каждая ячейка
соответствует одному из
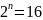состояний.
Рис. 2. Состояния регистров
Для того чтобы
измерить регистры
и
необходимо
нажать на одну из подсвеченных ячеек
регистров.
Рис. 3. Измеренные значения
Выполним постквантовую обработку. Для этого рассчитаем значения параметров
и
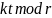согласно формулам:
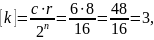
Проверим, что
.
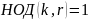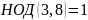– выполняется.
Рассчитаем
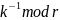с помощью расширенного алгоритма
Евклида:
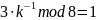
3 = 1 * 2 + 1
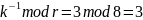
Проверка:
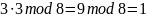
Зная
,
найдем значение дискретного логарифма
:
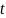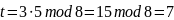
Выполним проверку:
,
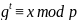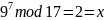
Рассчитанное значение соответствует заданному, следовательно дискретный логарифм найден верно.
Часть 2. Атака на секретный ключ криптосистемы Эль-Гамаля
Таблица 3. Исходные данный дискретное логарифмирование
-
№
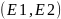
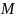
7 (19)
4
3
31
10, 11
13
Открытый ключ: (x, g, p) = (3, 4, 31)
Сложность схемы Эль-Гамаля определяется сложностью вычисления дискретного логарифма, так как
.
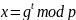С помощью программы QuantumDLOGSimulator.exe,
являющейся симулятором квантового
компьютера, вычислим закрытый ключ
t по открытому
ключу (x, g,
p). Так, как g
– первообразный корень p,
то
.
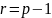Вводим необходимые параметры и нажимаем
кнопку «Рассчитать».