4

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4

ИССЛЕДОВАНИЕ ПОБОЧНЫХ АТАК НА КРИПТОСИСТЕМУ РША

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Выполнил студент 3 курса:

Травкина Е.А., ИКБ-14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д.т.н., проф. Яковлев В.А.

(Ф.И.О., № группы) (подпись)

Цель работы

Изучить влияние параметров и способов проектирования криптосистемы РША на возможность ее криптоанализа, используя побочные атаки, а также закрепить знания, полученные на лекциях курса «Основы криптографии с открытым ключом» , «Криптографические протоколы».

Порядок выполнения

1. Запустили программу «RSA attacks lab.exe».

2. Сгенерировали 3 набора ключей РША с одинаковой малой открытой экспонентой e=3. Длинна ключа РША = 16

Набор ключей	Модуль n	Экспонента e	Экспонента d	Простое p	Простое q
3	5459	3	8413	47	179
2	6583	3	4219	29	227
1	9553	3	6187	233	41

3.Сгенерировали случайное сообщение и зашифровали его.

Шифруемое сообщение: 3965

Криптограмма 1: 4258

Криптограмма 2: 6303

Криптограмма 3: 5900

4. Вычислили решение системы сравнений, используя китайскую теорему об остатках.

Общее решение системы сравнений: 62334657125

5. Нашли кубический корень методом Ньютона из решения системы, полученного на предыдущем шаге. Убедились в том, что это и есть исходное сообщение, сгенерированное в п.3.

Кубический корень: 3965

Сообщение: 3965

6. Переключили на окно демонстрации атаки при малом количестве возможных сообщений (см. Рис. 1).

7. Сгенерировали ключи криптосистемы и список возможных сообщений заданной длины (см. Рис. 1).

8. Зашифровали случайным образом одно из возможных сообщений (см. Рис. 1).

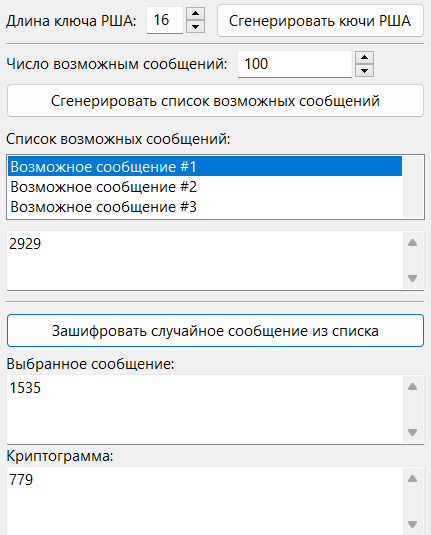
Рис. 1. Пункты 6 – 8

9. Путем последовательного шифрования возможных сообщений по списку и сравнения с криптограммой из п.8 нашли исходное сообщение (см. Рис. 2). Оценили скорость выполнения данной атаки в зависимости от количества возможных сообщений и длины модуля.

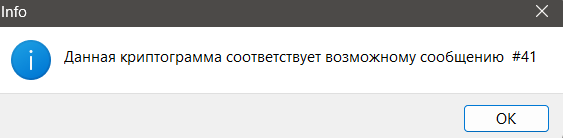
Рис. 2. Пункт 9

Скорость выполнения зависит от количества сообщений и того какое сообщение по порядку. Программа проверила 41 сообщения из 100, прежде чем криптограммы совпали. Если бы было зашифровано последнее сообщение из списка, то программа перебрала бы все сообщения, прежде чем найти нужное.

10. Переключили на окно демонстрации атаки Винера (атака на малую секретную экспоненту) (см. Рис. 3).

11. Сгенерировали ключи криптосистемы (см. Рис. 3).

12. Выполнили атаку Винера. Убедились в том, что найденные в результате выполнения атаки секретная экспонента и делители модуля криптосистемы действительно соответствуют параметрам заданной криптосистемы (см. Рис. 3). Атаку Винера подтвердить расчетами, взяв исходные данные из программы. (см. комментарии к подготовке отчета).

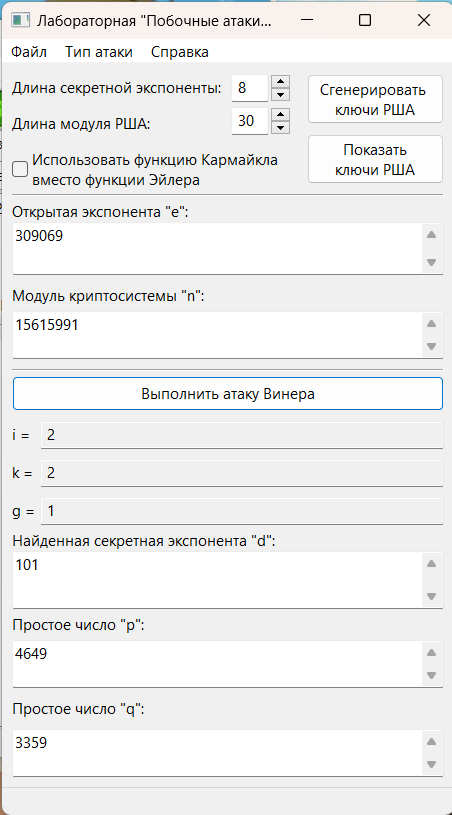
Рис. 3. Пункты 10 – 12

Подход Винера

Секретная экспонента может быть вычислена как знаменатель подходящей дроби в неравенстве

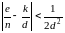
Мы получили :

Используя алгоритм Евклида для вычисления НОД, находим цепную дробь рационального числа

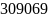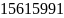= * 0 +

= *50 + 162541

= 162541 * 1 + 146528

162541= 146528 * 1 + 16013

146528 = 16013 * 9 +2411

16013 = 2411 * 6 + 1547

2411= 1547 * 1 + 864

1547 = 864 * 1 + 683

864 = 683 * 1 + 181

683 = 181 * 3 + 140

181 = 140 * 1 + 41

140 = 41 * 3 + 17

41 = 17 * 2 + 7

17 = 7 * 2 + 3

7 = 3 * 2 + 1

3 = 1 * 3 + 0

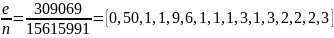
Вычисляем подходящие дроби:

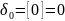
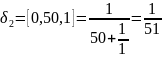
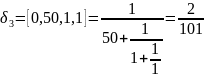
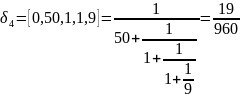и т.д. …

Далее перебором для каждой 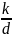подходящей дроби, вычисляем функцию Эйлера согласно выражению:

и решаем квадратное уравнение 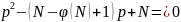. Проверяется, является ли р – простым.

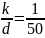1. Пусть , тогда k=1; d=50

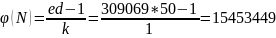
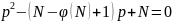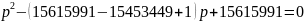=> , значения р будут нецелыми действительными.

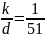2. Пусть , тогда k=1; d=51

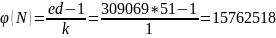
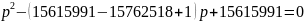=> , значения р будут нецелыми действительными.

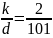3. Пусть , тогда k=2; d=101

=>

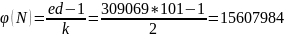
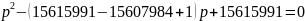
Р₁ = 3359; Р₂=4649, отсюда Р = 3359; q =

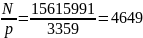
Проверка: q*p =

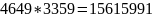
Следовательно, секретная экспонента d = 101, i = 2, k = 2, g = 1 найдена правильно.

13. Задавая различные длины модуля и секретной экспоненты, убедились в том, что атака Винера дает результат при битовой длине секретной экспоненты приблизительно меньше четверти битовый длины модуля криптосистемы (см. Рис. 4).

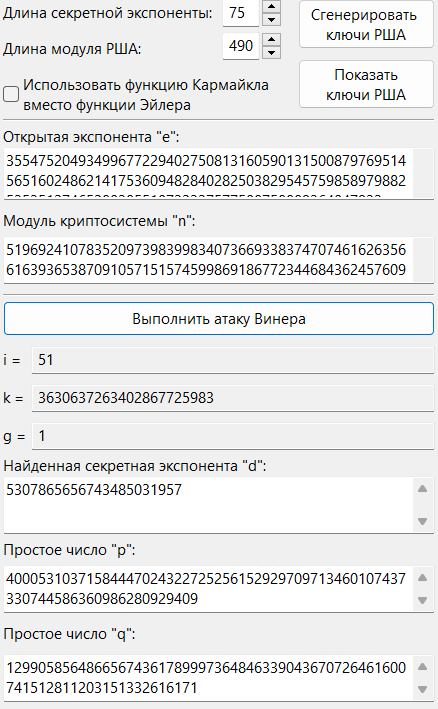
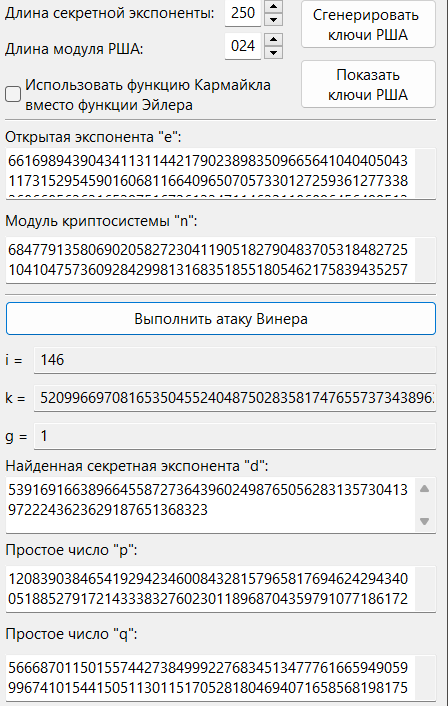
Рис. 4. Пункт 13

14. Переключились на окно демонстрации атаки, связанной с мультипликативным свойством шифра РША (см. Рис. 5).

15. Сгенерировали ключи криптосистемы (см. Рис. 5).

16. Сгенерировали случайное сообщение M и зашифровали его (см. Рис. 5).

17. Сгенерировали случайное число x взаимно простое с модулем криптосистемы и вычислили специальную криптограмму C' (см. Рис. 5).

18. Дешифровали C', получив тем самым некое сообщение M' (см. Рис. 5).

19. Извлекли исходное сообщение M из M'. Убедились в том, что полученное в результате выполнения атаки сообщение совпадает с исходным сообщением из п.13 (см. Рис. 5).

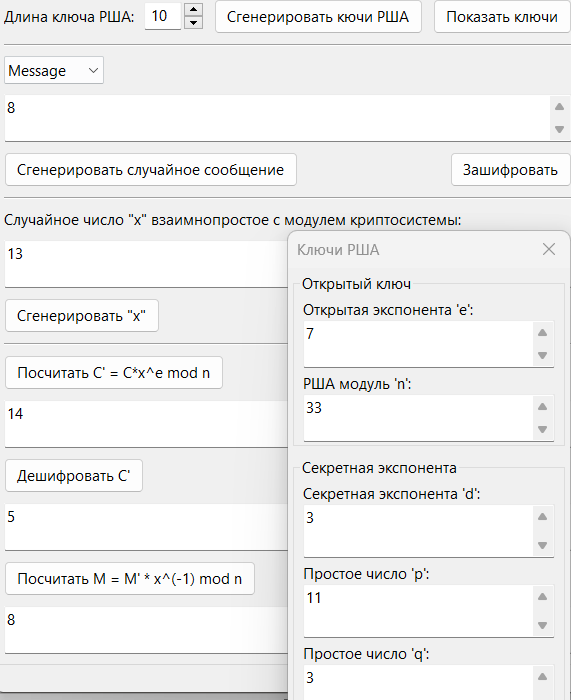
Рис. 5. Пункт 14 – 19

20. Переключили на окно демонстрации циклической атаки (см. Рис. 6).

21. Сгенерировали ключи криптосистемы (см. Рис. 6).

22. Сгенерировали случайное сообщение и зашифровали его (см. Рис. 6).

23. Выполнили циклическую атаку. Убедились в том, что найденное сообщение соответствует исходному сообщению из п.22 (см. Рис. 6).

24. Увеличив длину модуля криптосистемы, убедились в том, что алгоритм выполнения данной атаки обладает не полиномиальной сложностью (см. Рис. 6).

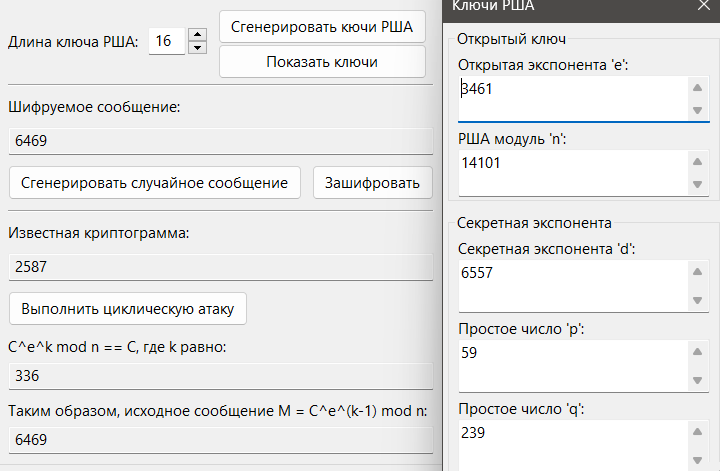
Рис. 6. Пункт 20 – 24

25. Переключили на окно демонстрации атаки на общие модули (см. Рис. 7).

26. Сгенерировали 2 набора ключей с общим модулем (см. Рис. 7).

27. Выполнили факторизацию общего модуля, зная обе секретные экспоненты (см. Рис. 7).

28. Вычислили секретную экспоненту второго набора ключей, зная делители общего модуля криптосистемы. Просмотрев исходные параметры обоих наборов ключей и результаты выполнения атаки, убедились в том, что атака на общие модули привела к взлому криптосистемы (см. Рис. 7).

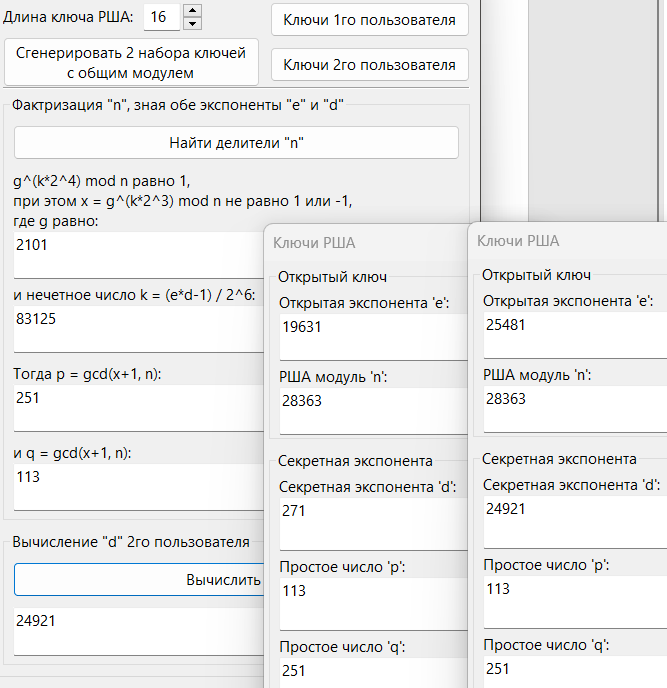
Рис. 7. Пункты 25 – 28

Вычисленная секретная экспонента d2 (d1 = 271, d2 = 24921) соответствует секретной экспоненте второго набора ключей.

Вывод

В ходе лабораторной работы изучили влияние параметров и способов проектирования криптосистемы РША на возможность ее криптоанализа, используя побочные атак. Закрепили знания, полученные на лекциях курса «Основы криптографии с открытым ключом», «Криптографические протоколы».

Санкт-Петербург

2024