3

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3

Криптосистема Рабина

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Выполнил студент 3 курса:

Травкина Е.А., ИКБ-14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д.т.н., проф. Яковлев В.А.

(Ф.И.О., № группы) (подпись)

Цель работы

Закрепить знания, полученные на лекциях по теме “Криптосистема Рабина”.

1 задание

Для шифрования найти открытый ключ - n, определить количество двоичных разрядов в нем- 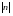. Разбить сообщение на блоки длиной двоичных разрядов. Зашифровать каждый блок, представив его десятичным числом. Расшифровать второй блок криптограммы.

№	p	q
19	11	17

1. Зашифровать сообщение: 119219319

2. Найдем открытый ключ n:

n = p*q = 17*11 = 187

3. Количество двоичных разрядов |n|:

128<187<256;

2⁷<187<2⁸

|n| = 8

4. Разобьем сообщение на блоки длиной |n| - 1 = 7 двоичных разрядов:

119219319₁₀ → 0111000 1101100 1001000 1110111

5. Зашифруем каждый блок, представив его десятичным числом:

M₁ = 0111000₂ = 56:

C₁ = m₁² mod 187 = 56² mod 187 = 144

M₂ = 1101100₂ = 108:

C₂ = m₂² mod 187 = 108² mod 187 = 70

M₃ = 1001000₂ = 72:

C₃ = m₃² mod 187 = 72² mod 187 = 135

M₄ = 1110111₂ = 119:

C₄ = m₄² mod 187 = 119² mod 187 = 136

Полученная криптограмма: {144, 70, 135, 136}

6. Расшифруем второй блок криптограммы C₂ = 70:

Найдем коэффициенты Безу y_p, y_q:

17 = 11*1+6; 6 = 17 – 11

11 = 6*1+5; 5 = 11 – 6

6 = 5*1 +1; 1 = 6 – 5

1 = 6 – 5 = 17 – 11 – (11 – 6) = 17 – 11 – 11 + 17 – 11 = 2*17 – 3*11

Y_p = -3; y_q = 2

7. Проверим p и q:

Так как 17 = 4*K+1 используем алгоритм Чипполе:

M_p =

b = 12

M_p = = mod 17

= (

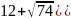
M_p = 6

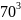M_q = mod p = mod 11 = mod 11 = 9

M_q = ±9

8. Находим 4 числа:

x₁ = (y_p*p*m_q + y_q*q*m_p) mod n = ( -3*11*6 + 2*17*9) mod 187 = 108

x₂ = n – x₁ = 187 – 108 = 79

x₃ = (y_p*p*m_q - y_q*q*m_p) mod n = ( -3*11*6 – 2*17*9) mod 187 = 57

x₄ = n – x₃= 187 – 57 = 130

Получили исходное сообщение второго блока криптограммы m₂ = 108

Задание 2.

№	М	С
19	110	25

1. Расшифровать криптограмму C=25, при известном ключе p=23, q=7, исходное сообщение M=110.

Проверим, есть ли у задачи решение:

НОД (23,7) = 1

Числа p и q простые.

23 mod 4 = 3

7 mod 4 = 3

2. Находим коэффициенты Безу:

23 = 7*3 + 2 2 = 23 – 7*3

7 = 2*3 + 1 1 = 7 – 2*3 = 7 – (23 – 7*3) *3 = 7*10 – 23*3

23*(-3) + 7*10 = 1

y_p = -3; y_q = 10

3. Используя китайскую теорему об остатках, вычислим четыре числа, среди которых одно будет являться истинным исходным сообщением.

m_p = 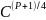mod p = mod 23 = mod 23 = 18

m_p = 18

m_q=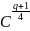 mod q= mod7=

m_p = 2

4. Найдем 4 корня:

n = p*q = 23*7 = 161

x₁ = (y_p*p*m_q + y_q*q*m_p) mod n = ((-3)*23*2 + 10*7*18) mod 161 = 156

x₂ = n – x₁ = 161 – 156 = 5

x₃ = (y_p*p*m_q - y_q*q*m_p) mod n = ((-3)*23*2 - 10*7*18) mod 161 = 110

x₄ = n – x₃ = 161 – 110 =51

Среди 4х корней получили исходное сообщение M = 110.

Вывод

В ходе выполнения лабораторной работы были закреплены знания по теме «Криптосистема Рабина», зашифровано сообщение в КС Рабина, а также произведено дешифрование криптограммы при известном закрытом ключе.

Санкт-Петербург

2024