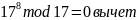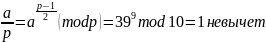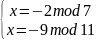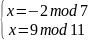МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
Дисциплина Криптографические протоколы
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2
ТЕСТИРОВАНИЕ ПРОСТЫХ ЧИСЕЛ И НАХОЖДЕНИЕ КВАДРАТИЧНЫХ ВЫЧЕТОВ
(тема отчета)
Направление/специальность подготовки
10.03.01 Информационная безопасность
(код и наименование направления/специальности)
Выполнил студент 3 курса:
Травкина Е.А., ИКБ-14
(Ф.И.О., № группы) (подпись)
Преподаватель:
д.т.н., проф. Яковлев В.А.
(Ф.И.О., № группы) (подпись)
Цель работы
Закрепить знания, полученные на лекциях лисциплины «криптопротоколы» по разделам: “Квадратичные вычеты” и “Генерирование и тестирование простых чисел”.
Задание 1.
1.Перейти к пакету “Maxima”.
2.Рассчитать вероятность попадания на простое число при случайном генерировании чисел разрядности l=100, 300, 500 и 1000 при помощи следующей команды:
(%i2) l:100; lg(x) := log(x)/log(10); EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));
(%o2) 100
(%i3) log(x)
(%o3) lg(x) := -------
log(10)
(%i4) 89
(%o4) ----
4455
(%i5) l:300; lg(x) := log(x)/log(10); EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));
(%o5) 300
(%i6) log(x)
(%o6) lg(x) := -------
log(10)
(%i7) 269
(%o7) -----
40365
(%i8) l:500; lg(x) := log(x)/log(10); EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));
(%o8) 500
(%i9) log(x)
(%o9) lg(x) := -------
log(10)
(%i10) 449
(%o10) ------
112275
(%i11) l:1000; lg(x) := log(x)/log(10); EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));
(%o11) 1000
(%i12) log(x)
(%o12) lg(x) := -------
log(10)
(%i13) 899
(%o13) ------
449550
3.Для проверки числа на простоту тестом Ферма сгенерировать необходимое количество случайных 3-х разрядных чисел при помощи команды:
U:100+random(900);
и отобрать среди них не менее 3 нечетных чисел m, среди которых должно быть одно простое число
(%i17) U:100+random(900);
(%o17) 285
(%i18) U:100+random(900);
(%o18) 745
(%i19) U:100+random(900);
(%o19) 191
Сгенерировать не менее 5 случайных 2-х разрядных чисел a при помощи команды:
U:10+random(90);
(%i23) U:10+random(90);
(%o23) 53
(%i24) U:10+random(90);
(%o24) 35
(%i25) U:10+random(90);
(%o25) 15
(%i26) U:10+random(90);
(%o26) 70
(%i27) U:10+random(90);
(%o27) 16
Произвести проверку чисел m на простоту, используя тест Ферма при помощи команды:
power_mod(a,m-1,m);
(%i28) power_mod(53,284,285);
(%o28) 226
(%i29) power_mod(35,744,745);
(%o29) 195
(%i30) power_mod(15,190,191);
(%o30) 1
Сделать выводы о правильности (или нет) произведенного тестирования. Какова может быть вероятность ошибки в данном случае?
Программа выдала результат, что число 191 простое, а числа 745 и 285 составные.
Можно сделать вывод, что тестирование произведено верно. При использовании теста Ферма вероятность ошибки тестирования будет равна 1/2. Но стоит отметить, что тест Ферма не работает на числах Кармайкла.
4.Произвести тестирования числа Кармайклаm=561 по методу Ферма. Для этого сгенерировать необходимое количество случайных 2-х разрядных чисел по п. 3 и далее выбрать из них не менее 5 чисел a’ взаимно простых с 561, используя команды:
gcd(a’,561);
(%i33) U:10+random(90); gcd(U,561);
(%o33) 40
(%i34) (%o34) 1
(%i35) U:10+random(90); gcd(U,561);
(%o35) 79
(%i36) (%o36) 1
(%i37) U:10+random(90); gcd(U,561);
(%o37) 74
(%i38) (%o38) 1
(%i39) U:10+random(90); gcd(U,561);
(%o39) 47
(%i40) (%o40) 1
(%i41) U:10+random(90); gcd(U,561);
(%o41) 26
(%i42) (%o42) 1
Проверить число 561, используя тест Ферма по п. 3.
(%i45) power_mod(40,560,561);
(%o45) 1
(%i46) power_mod(79,560,561);
(%o46) 1
(%i47) power_mod(74,560,561);
(%o47) 1
(%i48) power_mod(47,560,561);
(%o48) 1
(%i49) power_mod(26,560,561);
(%o49) 1
Сделать вывод о возможности использования данного теста для таких чисел.
В ходе проверки программа показала, что число 561 простое, однако оно составное (3*11*17=561). Можно сделать вывод, что данный тест нельзя использовать для чисел Кармайкла.
5.Произвести тестирование на простоту одного из чисел m, сгенерированных в п.3 и число Кармайкла 561, по методу Миллера–Рабина при помощи команды:
(%i60) m:561; f:0; a:m-1; u:random(m-2); x:0; while mod(a,2)=0 do ( f:f+1, a:a/2); printf(false,"a:~d,",a) ; printf(false,"f:~d,",f) ; x:power_mod(u,a,m); for i:0 step 1 thru f do ( printf(true,"i:~d, x: ~d;",i,x), x:mod(x^2,m));
(%o60) 561
(%i61) (%o61) 0
(%i62) (%o62) 560
(%i63) (%o63) 3
(%i64) (%o64) 0
(%i65) (%o65) done
(%i66) (%o66) a:35,
(%i67) (%o67) f:4,
(%i68) (%o68) 78
(%i69) i:0, x: 78;i:1, x: 474;i:2, x: 276;i:3, x: 441;i:4, x: 375;(%o69) done
(%i70) m:745; f:0; a:m-1; u:random(m-2); x:0; while mod(a,2)=0 do ( f:f+1, a:a/2); printf(false,"a:~d,",a) ; printf(fals
e,"f:~d,",f) ; x:power_mod(u,a,m); for i:0 step 1 thru f do ( printf(true,"i:~d, x: ~d;",i,x), x:mod(x^2,m));
(%o70) 745
(%i71) (%o71) 0
(%i72) (%o72) 744
(%i73) (%o73) 185
(%i74) (%o74) 0
(%i75) (%o75) done
(%i76) (%o76) a:93,
(%i77) (%o77) f:3,
(%i78) (%o78) 155
(%i79) i:0, x: 155;i:1, x: 185;i:2, x: 700;i:3, x: 535;(%o79) done
Проделали тест для числа 745 пять раз.
Число 745 простое с вероятность ошибки p=1/45=0,0009765625.
Тест Миллера — Рабина позволяет эффективно определить, является ли число простым или составным, однако данный тест - вероятностный. Вероятность ошибки равна 1/4к.
6.Найти несколько квадратичных вычетов u<m по mod(m), где m одно из простых 3-х разрядных чисел, полученных в п. 5, используя вычисление символа Якоби ( который для простых mсовпадает с символом Лежандра) , при помощи следующей команды:
(%i159) u:233;m:745; jacobi(u,m);
(%o159) 233
(%i160) (%o160) 745
(%i161) (%o161) 1
(%i162) u:23;m:745; jacobi(u,m);
(%o162) 23
(%i163) (%o163) 745
(%i164) (%o164) 1
(%i165) u:14;m:745; jacobi(u,m);
(%o165) 14
(%i166) (%o166) 745
(%i167) (%o167) - 1
(%i168) u:73;m:745; jacobi(u,m);
(%o168) 73
(%i169) (%o169) 745
(%i170) (%o170) - 1
Задание 2
Распределите числа в поле gf(p) на вычеты и невычеты.
р=17 для нечетных вариантов
При С=1 |
(%i180) C:1; p:17; jacobi(C,p); (%o180) 1 (%i181) (%o181) 17 (%i182) (%o182) 1 |
|
При С=2 |
(%i177) C:2; p:17; jacobi(C,p); (%o177) 2 (%i178) (%o178) 17 (%i179) (%o179) 1 |
|
При С=3 |
(%i183) C:3; p:17; jacobi(C,p); (%o183) 3 (%i184) (%o184) 17 (%i185) (%o185) - 1 |
|
При С=4 |
(%i186) C:4; p:17; jacobi(C,p); (%o186) 4 (%i187) (%o187) 17 (%i188) (%o188) 1 |
|
При С=5 |
(%i189) C:5; p:17; jacobi(C,p); (%o189) 5 (%i190) (%o190) 17 (%i191) (%o191) - 1 |
|
При С=6 |
(%i192) C:6; p:17; jacobi(C,p); (%o192) 6 (%i193) (%o193) 17 (%i194) (%o194) - 1 |
|
При С=7 |
(%i195) C:7; p:17; jacobi(C,p); (%o195) 7 (%i196) (%o196) 17 (%i197) (%o197) - 1 |
|
При С=8 |
(%i198) C:8; p:17; jacobi(C,p); (%o198) 8 (%i199) (%o199) 17 (%i200) (%o200) 1 |
|
При С=9 |
(%i201) C:9; p:17; jacobi(C,p); (%o201) 9 (%i202) (%o202) 17 (%i203) (%o203) 1 |
|
При С=10 |
(%i204) C:10; p:17; jacobi(C,p); (%o204) 10 (%i205) (%o205) 17 (%i206) (%o206) - 1 |
|
При С=11 |
(%i207) C:11; p:17; jacobi(C,p); (%o207) 11 (%i208) (%o208) 17 (%i209) (%o209) - 1 |
|
При С=12 |
(%i210) C:12; p:17; jacobi(C,p); (%o210) 12 (%i211) (%o211) 17 (%i212) (%o212) - 1 |
|
При С=13 |
(%i213) C:13; p:17; jacobi(C,p); (%o213) 13 (%i214) (%o214) 17 (%i215) (%o215) 1 |
|
При С=14 |
(%i216) C:14; p:17; jacobi(C,p); (%o216) 14 (%i217) (%o217) 17 (%i218) (%o218) - 1 |
|
При С=15 |
(%i219) C:15; p:17; jacobi(C,p); (%o219) 15 (%i220) (%o220) 17 (%i221) (%o221) 1 |
|
При С=16 |
(%i222) C:16; p:17; jacobi(C,p); (%o222) 16 (%i223) (%o223) 17 (%i224) (%o224) 1 |
|
При С=17 |
(%i225) C:17; p:17; jacobi(C,p); (%o225) 17 (%i226) (%o226) 17 (%i227) (%o227) 0 |
|
Проверьте, является ли число а=(№вар+20)mod31 вычетом по модулю 17, 19. A=39
(%i228) C:39; p:17; jacobi(C,p); (%o228) 39 (%i229) (%o229) 17 (%i230) (%o230) - 1 |
|
(%i231) C:39; p:19; jacobi(C,p); (%o231) 39 (%i232) (%o232) 19 (%i233) (%o233) 1 |
|
Решите уравнение

(Вариант №19)
р=23, a=41
Проверим, что уравнение имеет решение:
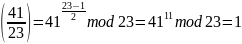
P=23=4*5+3, т.к. вид p = 4k + 3, то корень находится просто



р=29, a=36

В данном случае применим алгоритм Чиполлы.
Найдем случайное число b, такое, что b2 – a – невычет.
(%i250) p:29; a:36; b:random(p-1); jacobi(b^2-a,p);
(%o250) 29
(%i251) (%o251) 36
(%i252) (%o252) 27
(%i253) (%o253) - 1
b=27


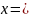
 =
1 + 17
=
1 + 17
= 11+5
(2046+110 )mod 29= 16+23
(1+17
)(11+5 16+23
)(
16+23
)( = 47554716+5489004
mod
29 = 23
= 47554716+5489004
mod
29 = 23
X = +23; -23
Проверка:


Решите все решения уравнение

Для n=7*11, для вариантов 13-19, a=81
Вариант №19

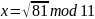




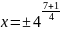 =
=

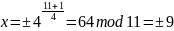
Получим 4 системы уравнений:
1)
|
3)
|
2)
|
4)
|
Решение 1-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x=x0 mod M, где М = m1∙ m2.

M = m1∙ m2 = 7∙ 11 = 77
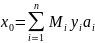
x0 = M1y1a1 + M2y2a2

Miyi = 1mod mi
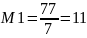 ;
;

M1y1 = 1 mod m1 M2y2 = 1 mod m2
11y1 = 1 mod 7 7y2 = 1 mod 11 y1 =2 y2 = 8
x0 = 11∙2∙2 + 7∙8∙9 = 548
x = x0 mod M
x = 548 mod 77 = 9
Решение 2-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x = x0 mod M, где М = m1∙ m2
M = m1∙ m2 = 7∙ 11 = 77
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
11y1 = 1 mod 7 7y2 = 1 mod 11 y1 =2 y2 = 8
x0 = 11∙2∙(-2) + 7∙8∙(-9) = -548
x = x0 mod M
x = -548 mod 77 = 68
Решение 3-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x = x0 mod M, где М = m1∙ m2
M = m1∙ m2 = 7∙ 11 = 77
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
11y1 = 1 mod 7 7y2 = 1 mod 11 y1 =2 y2 = 8
x0 = 11∙2∙2 + 7∙8∙(-9) = -460
x = x0 mod M
x = -460 mod 77 = 2
Решение 4-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x=x0 mod M, где М= m1∙ m2
M = m1∙ m2 = 7∙ 11 = 77
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
11y1 = 1 mod 7 7y2 = 1 mod 11 y1 =2 y2 = 8
x0 = 11∙2∙(-2) + 7∙8∙9 = 460
x = x0 mod M
x = 460 mod 77 = 75
Проверка:
x1: 92mod 77 = 81mod 77 =4
x2: 682mod 77 = 4624mod 77 = 4
x3: 22mod 77 = 4mod 77 = 4
x4: 752mod 77 = 5625mod 77 = 4
Ответ: х1 = 9; х2 = 68; х3 = 2; х4 = 75;
Вывод
В ходе выполнения лабораторной работы были закреплены знания по разделам «Квадратичные вычеты» и «Генерирование и тестирование простых чисел».


 вычет
вычет


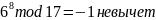

 вычет
вычет